Министерство высшего и профессионального образования Российской Федерации

Уральский государственный технический университет - УПИ

Теория поля

Задания для самостоятельной работы

по курсу " Высшая математика" для

студентов всех форм обучения всех

специальностей

Екатеринбург, 2002

УДК 517

Составители Д.Х.Даянов, Е.М.Пампура, М.А.Вигура, И.П.Ишунькина, Н.В.Колмогорова, Н.Г.Рыжкова

Научный редактор проф.,докт.физ.-мат. наук А.Б.Соболев

Теория поля: Задания для самостоятельной работы по курсу " Высшая математика" / Д.Х.Даянов, Е.М.Пампура, М.А.Вигура, И. П.Ишунькина, Н.В. Колмогорова, Н.Г.Рыжкова

Екатеринбург: УГТУ - УПИ, 2002. с.

Работа содержит ответы к домашним и контрольным заданиям по программному разделу курса. Содержит 12 задач в 31 вариантах.

Подготовлено кафедрой " Высшая математика".

Ó Уральский государственный

технический университет -УПИ, 2002

Вариант 1

Задача 1.1. Найти производную скалярного поля u(x,y,z) в точке М по направлению проходящей через эту точку нормали к поверхности S,образующей острый угол с положительным направлением оси Oz.

Задача 2.1. Найти угол между градиентами скалярных полей u(x,y,z) и v(x,y,z) в точке М,где

Задача 3.1. Найти векторные линии в векторном поле ,

Задача 4.1. Найти поток векторного поля через часть поверхностиS, вырезаемую плоскостями (нормаль внешняя к замкнутой поверхности, образуемой данными поверхностями),

Задача 5.1. Найти поток векторного поля через часть плоскости Р, расположенную в первом октанте (нормаль образует острый угол с осьюOz),

Задача 6.1. Найти поток векторного поля через часть плоскостиP, расположенную в первом октанте (нормаль образует острый угол с осью Oz,

Задача 7.1. Найти поток векторного поля через замкнутую поверхностьS (нормаль внешняя).

Задача 8.1. Найти поток векторного поля через замкнутую поверхностьS (нормаль внешняя).

Задача 9.1. Найти поток векторного пол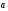я через замкнутую поверхностьS (нормаль внешняя).

Задача 10.1. Найти работу силы F при перемещении вдоль линии L от точки М к точке N.

Задача 11.1. Найти циркуляцию векторного поля вдоль контура Г (в направлении, соответствующем возрастанию параметра t).

Задача 12.1. Найти модуль циркуляции векторного поля вдоль контура Г.

Вариант 2

Задача 1.2. Найти производную скалярного поля u(x,y,z) в точке М по направлению проходящей через эту точку нормали к поверхности S,образующей острый угол с положительным направлением оси Oz.

Задача 2.2. Найти угол между градиентами скалярных полей u(x,y,z) и v(x,y,z) в точке М, где

Задача 3.2. Найти векторные линии в векторном поле ,

Задача 4.2. Найти поток векторного поля через часть поверхностиS, вырезаемую плоскостями (нормаль внешняя к замкнутой поверхности, образуемой данными поверхностями),

Задача 5.2. Найти поток векторного поля через часть плоскости Р, расположенную в первом октанте (нормаль образует острый угол с осьюOz),

Задача 6.2. Найти поток векторного поля через часть плоскостиP, расположенную в первом октанте (нормаль образует острый угол с осью Oz,

Задача 7.2. Найти поток векторного поля через замкнутую поверхностьS (нормаль внешняя).

Задача 8.2. Найти поток векторного пол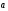я через замкнутую поверхностьS (нормаль внешняя).

Задача 9.2. Найти поток векторного пол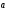я через замкнутую поверхностьS (нормаль внешняя).

Задача 10.2. Найти работу силы F при перемещении вдоль линии L от точки М к точке N.

Задача 11.2. Найти циркуляцию векторного поля вдоль контура Г (в направлении, соответствующем возрастанию параметра t).

Задача 12.2. Найти модуль циркуляции векторного поля вдоль контура Г.