5.6. Главные оси инерции и главные моменты инерции

При изменении угла изменяются. Найдём значение угла, при которомиимеют экстремальные значения. Для

возьмём первую производную от пои приравняем её нулю.

.

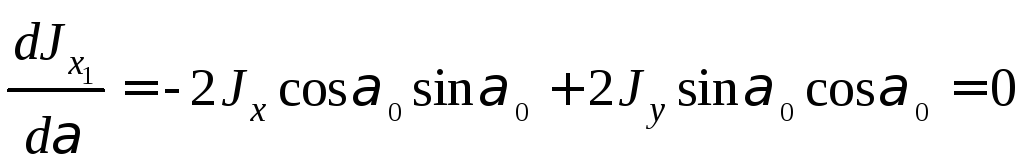Или можно записать:

откуда получаем

. (5.23)

Эта формула определяет положение двух осей, относительно которых один осевой момент инерции максимальный, другой - минимальный.

Такие оси называются главными. Моменты инерции относительно главных осей называются главными моментами инерции.

Значения главных моментов инерции найдём из формул (5.18) и (5.19), подставив в них из формулы (5.23):

. (5.24)

По своей структуре эта формула аналогична формуле для главных напряжений.

Покажем, что относительно главных осей инерции центробежный момент равен нулю. Приравняем нулю из формулы (5.20):

,

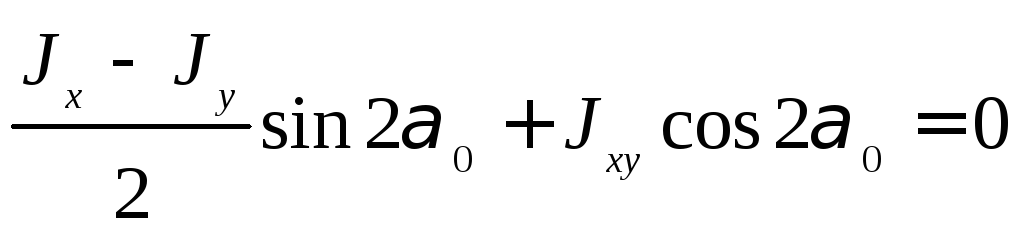откуда

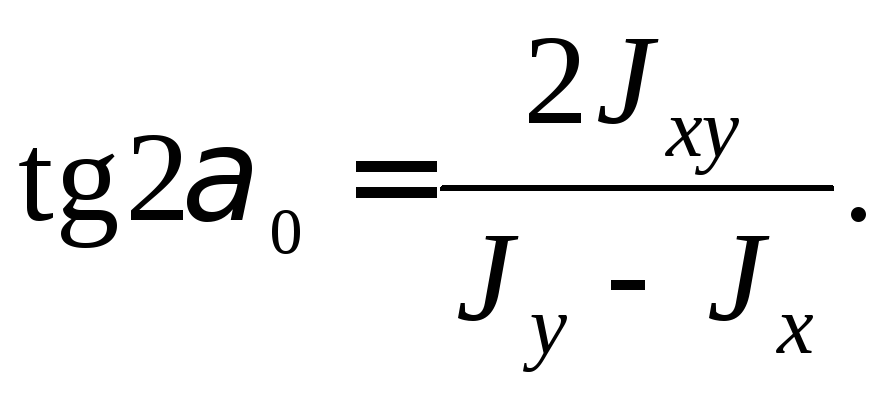
5.7. Зависимость между моментами инерции относительно

параллельных осей

Момент инерции сложной фигуры равен сумме моментов её составных частей:

(5.25)

где – моменты инерции частей сложной фигуры относительно осих.

Выражение (5.25) следует из свойства определённого интеграла

где А – площадь всей фигуры; – площади каждой части фигуры.

Таким образом, для вычисления момента инерции сложного поперечного сечения его необходимо разбить на ряд простых фигур, вычислить момент инерции относительно оси каждой фигуры и затем все моменты инерции просуммировать. Для определения осевого момента инерции сложного по конфигурации поперечного сечения необходимо иметь формулу перехода для моментов инерции при параллельном переносе оси.

Оси, проходящие через центр тяжести фигуры, называются центральными осями, а момент инерции, определённый относительно центральной оси, называется центральным моментом инерции.

Положим, что х – центральная ось, момент инерции относительно которой нам известен. Определим момент инерциифигуры относительно оси, параллельной центральной и отстоящей от неё на расстоянииа (рис. 5.8):

.

Расстояния всех элементарных площадок dA от оси будет больше на постоянную величинуа, т.е.

Рис. 5.8

Первый интеграл представляет собой центральный момент инерции. Второй интеграл равен нулю, так как это статический момент площади фигуры относительно оси, проходящей через центр тяжести с. Третий интеграл равен Следовательно,

(5.26)

Формула (5.26) широко применяется в практике и читается следующим образом: момент инерции сечения относительно какой – либо оси равен сумме момента инерции относительно центральной оси, ей параллельной, и произведению площади всего сечения на квадрат расстояния между осями.

Отметим, что момент инерции прокатных сечений (двутавров, швеллеров, уголков и др.) приведены в таблицах сортамента.

5.8. Зависимость между центробежными моментами инерции

относительно двух систем параллельных осей

Пусть центральные оси (рис. 5.9) и центробежный момент инерцииизвестны. Найдём центробежный момент инерции относительно осейи:

следовательно

Второй и третий интегралы равны 0, так как являются статическими моментами относительно центральных осей. Окончательно:

. (5.27)

Рис. 5.9

Центробежный момент инерции относительно системы взаимно перпендикулярных осей, параллельных центральным, равен центробежному моменту инерции относительно центральных осей плюс произведение площади фигуры на координаты её центра тяжести относительно новых осей.

6. СДВИГ И КРУЧЕНИЕ