5.2. Моменты инерции плоских сечений

Полярным моментом инерции сечения называется сумма произведений элементарных площадок(dA) на квадраты их расстояний () до какого-либо полюса, лежащего в плоскости сечения, распространённая на всю площадь сечения (рис. 5.2):

. (5.7)

Рис. 5.2

Осевым моментом инерции площади сечения относительно какой-либо оси, лежащей в её плоскости, называется сумма произведений элементарных площадок на квадраты расстояний их до этой оси:

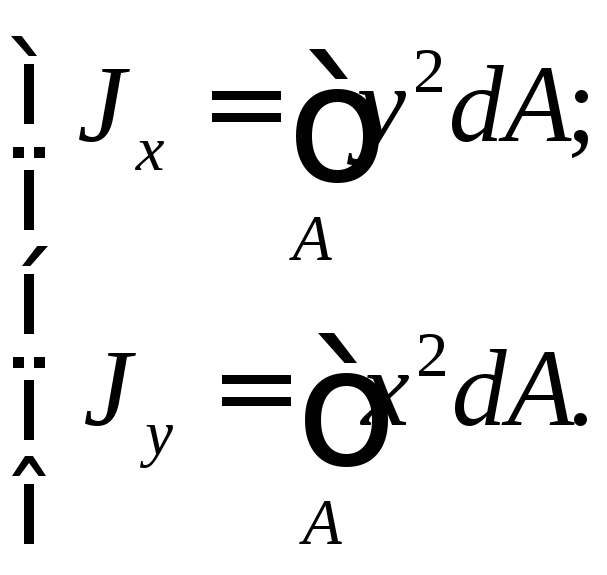(5.8)

Из рис. 5.2 видно, что Подставим это выражение в (5.7) и получим

(5.9)

Следовательно, сумма осевых моментов инерции плоского сечения относительно двух перпендикулярных осей равна полярному моменту инерции относительно полюса, представляющего точку пересечения этих осей.

Осевые и полярные моменты инерции измеряются в метрах в четвертой степени (м⁴). Они всегда положительны и не могут быть равны нулю.

5.3. Моменты инерции простых плоских сечений

Определим моменты инерции наиболее распространенных плоских сечений.

1. Прямоугольник (рис. 5.3). Вычислим момент инерции сечения относительно оси х, проходящей через центр тяжести параллельно основанию. Выделим на расстоянии у от оси х бесконечно узкую площадку высотой dy, тогда dA=b dy. В соответствии с (5.8):

. (5.10)

Рис. 5.3

Аналогично находим осевой момент инерции относительно оси у:

(5.11)

Для квадратного сечения со стороной а:

(5.12)

2. Круг радиуса r (рис. 5.4). Определим вначале полярный момент инерции относительно центра круга. За dA примем площадь бесконечно тонкого кольца толщиной и радиусом, тогдаПодставим это значение в (5.7):

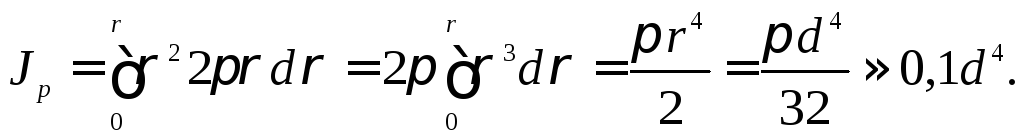(5.13)

Определим теперь осевые моменты инерции. Согласно формуле (5.9) для круглого сечения

Следовательно,

(5.14)

Рис. 5.4

3. Кольцо (рис. 5.5). Воспользуемся формулой (5.13), приняв пределы интегрирования от R до r.

Рис. 5.5

Обозначим отношение . Тогда

(5.15)

Аналогично сплошному сечению (5.14) определим осевой момент инерции кольца:

(5.16)

5.4. Центробежный момент инерции

Центробежным моментом инерции называется сумма произведений элементарных площадок на их координаты, распространённая на всю площадь сечения (рис. 5.6)

. (5.17)

Рис. 5.6

Центробежный момент инерции имеет размерность – метр в четвертой степени (м⁴) и может быть величиной положительной, отрицательной и равной нулю.

Если взаимно перпендикулярные оси х и у или одна из них являются осями симметрии фигуры, то относительно таких осей центробежный момент инерции равен нулю.

5.5. Изменение моментов инерции при повороте осей

Найдём зависимость между моментами инерции относительно осей х и у и моментами инерции относительно осей ,, повёрнутых на угол

(рис. 5.7). Пусть J_x > J_y и положительный угол отсчитывается от осих против хода часовой стрелки.

Найдём зависимость между координатами площадки в исходных и повёрнутых осях.

,

.

Теперь определим моменты инерции относительно осей и:

Или

. (5.18)

.

После преобразований

. (5.19)

Рис. 5.7

Центробежный момент инерции

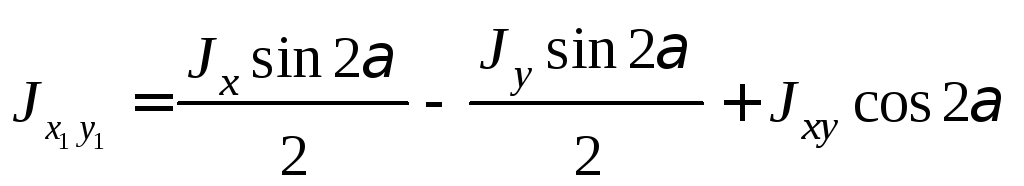. (5.20)

Сложим (5.18) и (5.19):

(5.21)

Вычтем (5.19) из (5.18):

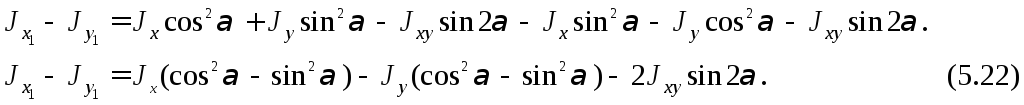
Анализ формулы (5.21): сумма моментов инерции относительно любых взаимно-перпендикулярных осей не меняется при их повороте.

Формула (5.22) может быть использована для определения центробежного момента инерции по известным осевым моментам инерции относительно осейх, у и