4.1. Напряжения в наклонных площадках при осевом растяжении

или сжатии

При растяжении прямого бруса в поперечных сечениях возникают только нормальные напряжения, определяемые по формуле

Для определения напряжений в наклонных сечениях при растяжении в одном направлении проведём наклонное сечение под углом (рис. 4.1).

Рис. 4.1 Рис. 4.2

Составим уравнение равновесия элементарной трёхгранной призмы

(рис. 4.2). Площадь наклонной грани dA.

, (4.1)

откуда .

, (4.2)

откуда .

Выводы

1) наибольшее нормальное напряжение возникает в поперечном сечении бруса:

;

2) наибольшее касательное напряжение возникает на площадке, наклонённой под углом ик оси бруса и равно половине нормального напряжения, возникающего в соответствующей точке поперечного сечения:

4.2. Напряжения на взаимно-перпендикулярных площадках

Определим нормальные и касательные напряжения на взаимно- перпендикулярных площадках (рис. 4.3).

;

.

Для взаимно-перпендикулярной площадки:

;

.

Рис. 4.3

Анализируя полученные результаты, можно сделать вывод:

. (4.3)

Сумма нормальных напряжений на двух взаимно – перпендикулярных площадках постоянна и равна главному напряжению.

(4.4)

т.е. на двух взаимно-перпендикулярных площадках действуют равные по величине и обратные по знаку касательные напряжения (закон парности касательных напряжений).

4.3. Определение напряжений в наклонных сечениях при

растяжении или сжатии по двум взаимно-перпендикулярным

направлениям

При плоском напряженном состоянии

Между направлениеми площадкой угол равен(рис. 4.4).

Рис. 4.4 Рис. 4.5

Напряжения ив произвольном наклонном сечении можно определить из равновесия трёхгранной призмыABC (рис. 4.5) или по полученным формулам, суммируя напряжения от действия и(при замене углана).

,

откуда . (4.5)

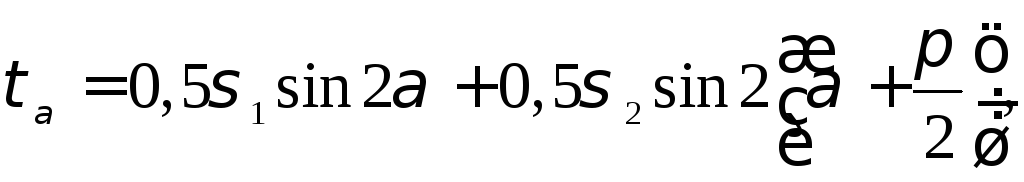
откуда . (4.6)

Из формулы (4.6) видно, что максимальные касательные напряжения равны полуразности главных напряжений

и действуют в сечениях, одинаково наклоненных к направлениям и, т.е. приили.

Для двухосного напряжённого состояния сохраняет свою силу закон парности касательных напряжений.

4.4. Определение главных напряжений и главных площадок

напряжения, действующие по граням элемента (рис. 4.6). Требуется определить положение главных площадок и значения главных напряжений. Рассмотрим равновесие трёхгранной призмы DBС (рис. 4.7). Примем, что Уголбудем отсчитывать от направления большего напряжения до нормали к площадке. За положительное направление примем направление против хода часовой стрелки. Площадь наклонной грани обозначимdA. Тогда площадь вертикальной грани dA , а горизонтальной –dA .

Рис. 4.6 Рис. 4.7

Проектируем все силы на ось N:

Проектируем все силы на ось Т:

Сократим на dA:

;

.

; (4.7) . (4.8)

Чтобы отыскать положение главных площадок, нужно либо приравнять нулю производную , либо приравнять нулю касательные напряжения, т.к. на главных площадках касательных напряжений нет.

,

откуда

(4.9)

Для определения экстремальных значений напряжений, т.е. главных напряжений, значение угла из формулы (4.9) подставим в формулу (4.7). Предварительно тригонометрические функции в формуле (4.7) выразим через тангенс двойного угла, используя известные формулы тригонометрии:

Далее вместо подставляем значение (4.9) и получаем формулу для определения главных напряжений:

(4.10)

Если одно из заданных нормальных напряжений равно нулю, то формула (4.10) примет вид:

(4.11)

Этой формулой будем пользоваться при изучении сложного сопротивления.

равны полуразности главных напряжений, следовательно,

Если одно из нормальных напряжений равно 0, то

(4.12)