3.2. Твёрдость

Для определения механических характеристик готовых деталей

невозможно использовать разрушающие методы контроля, к которым относится испытание на растяжение и ряд других. В производстве для проведения оперативного контроля применяются методы определения твёрдости.

Твёрдость – это свойство материала оказывать сопротивление внедрению в него другого, более твёрдого тела. Твёрдость тесно связана с показателями прочности и пластичности. Для определения твёрдости существует несколько способов, наиболее распространённые из которых – пробы по Бринеллю (НВ) и Роквеллу (HR). При определении твёрдости по Бринеллю в поверхность материала детали вдавливается стальной шарик

(рис. 3.3) и по величине отпечатка определяют число твёрдости. Во втором случае в материал вдавливается алмазный конус. Твёрдость по Бринеллю определяют вдавливанием в испытываемый материал закалённого шарика диаметром D = 10 мм силой F = 30 кН. Число единиц твёрдости по Бринеллю НВ равно отношению силы F, вдавливающей шарик, к площади поверхности полученного отпечатка:

(3.3)

Рис. 3.3

Для сталей зависимость между числом единиц твёрдости по Бринеллю НВ и пределом прочности с достаточной степенью точности определяется формулой

. (3.4)

Зависимость между твёрдостью по Бринеллю и Роквеллу:

(3.5)

3.3. Определение допускаемых напряжений и коэффициента запаса

прочности

Прочность, т.е. способность материала оказывать сопротивление механическим усилиям, является важнейшим критерием работоспособности элементов конструкций и деталей. Обычно под прочностью понимают сопротивление разрушению или пластическим деформациям.

Деформации определяются напряжениями. Расчётные напряжения должны быть такими, чтобы обеспечивалась прочность детали при минимальной затрате материала. Наиболее распространённым методом оценки прочности является сравнение расчётных напряжений, возникающих в деталях при действии эксплуатационных нагрузок с допускаемыми напряжениями. Условие прочности по допускаемому напряжению имеет вид

(3.6)

где – наибольшее напряжение в детали от наибольшей ожидаемой нагрузки;– допускаемое напряжение.

Аналогичное условие прочности можно записать и для касательных напряжений.

Определение допускаемого напряжения является важным этапом расчёта и проектирования, т. к. при большом значении возможно разрушение детали, а заниженные значенияприводят к тому, что деталь получается тяжёлой и более дорогой. Допускаемые нормальныеи касательныенапряжения при статических нагрузках и отсутствии концентрации напряжений определяют по формулам

; , (3.7)

где и– предельные значения напряжений, при которых деталь выходит из строя;– требуемый, заданный или нормативный коэффициент запаса прочности.

Распространённым методом оценки прочности является также сравнением действительного коэффициента запаса прочности s с допускаемым . В этом случае условие прочности выражается неравенством

(3.8)

Расчёт по допускаемым напряжениям обычно выполняют как проектный, служащий для определения размеров детали. Например, диаметр стержня, нагруженного внешней растягивающей силой F, можно определить из условия прочности следующим образом:

(3.9)

откуда

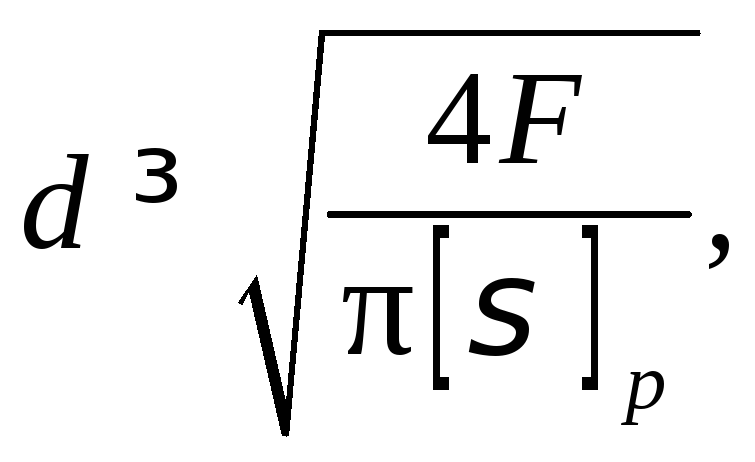(3.10)

где – допускаемое напряжение при растяжении.

Расчёт по запасу прочности выполняется как проверочный, уточнённый на той стадии, когда уже имеется чертёж детали и можно учесть концентраторы напряжений, обработку поверхности, размеры поперечных сечений и т.д.

Напряжения, возникающие в элементах конструкций, могут быть постоянными и переменными во времени. При расчётах на прочность при постоянных напряжениях детали из пластичных материалов в качестве предельного напряжения принимают предел текучести илиПри расчётах на прочность при постоянных напряжениях деталей из хрупких материалов в качестве предельного напряжения принимают соответствующий предел прочности

При расчётах на прочность деталей при переменных напряжениях в качестве предельного принимают соответствующий предел выносливости . Под пределом выносливости понимают наибольшее переменное напряжение, при действии которого не происходит разрушение образца после произвольно большого количества циклов нагружений.

Для выбора допускаемых напряжений и коэффициентов запаса прочности пользуются двумя методами: табличным и дифференциальным.

Табличный метод проще и удобнее для пользования. Поэтому во всех случаях, когда имеются специализированные таблицы допускаемых напряжений и коэффициентов запаса прочности, составленные для отдельных узлов и деталей машин, обычно используется этот метод. Например, для валов передач средних размеров принимают равным 2,5.

Дифференциальный метод заключается в том, что допускаемое напряжение или допускаемый коэффициент запаса прочности определяют по соответствующей формуле, которая учитывает различные факторы, влияющие на прочность рассчитываемой детали или конструкции. Допускаемый коэффициент запаса прочности рекомендуется определять по формуле

.

Здесь – учитывает точность определения действующих на конструкцию внешних нагрузок и возникающих в ней напряжений.при точных расчётах;при расчётах средней точности;

– учитывает однородность материала детали.= 1,2…1,5 для деталей из поковок и проката;для деталей из стального литья;для чугунных деталей;

– коэффициент безопасности детали.большие значения принимают для дорогостоящих и ответственных деталей, поломка которых может привести к серьёзной аварии.

4. СЛОЖНОЕ НАПРЯЖЁННОЕ СОСТОЯНИЕ