2.3. Определение деформаций

Для большинства конструкционных материалов при нагружении до определённых значений напряжений справедлива следующая зависимость между деформацией стержня и нормальным напряжением:

(2.3)

где ε - относительное удлинение стержня;;

- абсолютное удлинение стержня; – длина образца до деформации;

–длина образца после деформации (рис. 2.2).

Зависимость (2.3) носит название закона Гука и формулируется следующим образом: линейные деформации прямо пропорциональны нормальным напряжениям.

Коэффициент Е, зависящий от материала, называется модулем продольной упругости, или модулем упругости первого рода. Он характеризует жёсткость материала, т.е. его способность сопротивляться деформации. Поскольку – величина безразмерная, то единица измерения модуля продольной упругостиЕ та же, что и у напряжения , т.е. паскаль. В табл. 2.1 приведены значенияЕ для некоторых материалов [1].

Таблица 2.1

Материал	E, МПа	Материал	E, МПа
Сталь		Бронза
Медь		Титан
Чугун		Дерево
Алюминий		Стеклопластики

Поскольку и, из формулы (2.3) получаем выражение для определения абсолютного удлинения или укорочения стержня длиной:

(2.4)

Между продольной и поперечной деформациями существует зависимость

, (2.5)

где – относительное поперечное сужение стержня. Коэффициентназывается коэффициентом Пуассона или коэффициентом поперечной деформации. Значениедля различных материалов колеблется в пределах от 0 до 0,5. Для всех марок сталей можно принимать значение. Поскольку, то полное поперечное сужение (при растяжении) или уширение (при сжатии) определяется по формуле

,

где ∆b – абсолютная поперечная деформация; – первоначальный поперечный размер;– поперечный размер стержня после деформации.

В практике часто встречаются стержни переменного сечения, в основном – ступенчатые. У таких стержней полное изменение длины определяется как алгебраическая сумма деформаций его отдельных частей, в пределах которых величины Е, N и A постоянны:

В частности, для приведённой на рис. 2.3 схемы полное удлинение ступенчатого стержня определится как сумма деформаций двух участков:

т.к.

Рис. 2.3

2.4. Статически неопределимые задачи при осевом растяжении или

сжатии

Определить реакции и усилия в частях бруса и(рис. 2.4).

Сила F растягивает верхнюю часть бруса и сжимает нижнюю. Обозначим реакции заделки и.

Рис. 2.4

Уравнение равновесия:

Рассмотрим деформации. Поскольку концы бруса защемлены, то удлинение верхней части равно укорочению нижней, следовательно,

; или ,

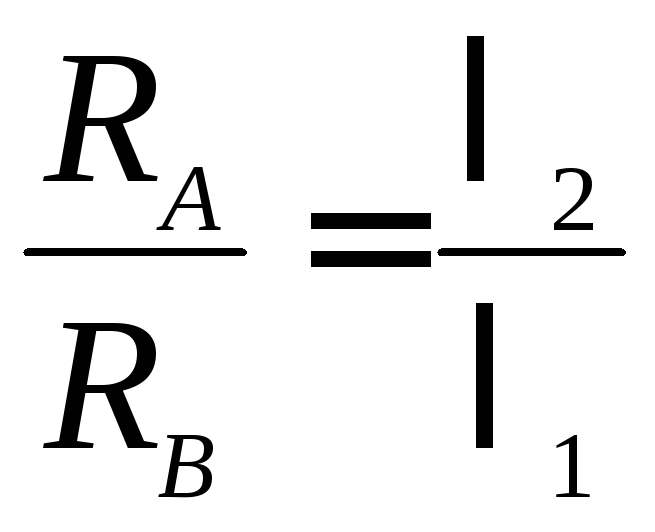т.е. реакции обратно пропорциональны длинам и.

Решаем это уравнение совместно с уравнением статики.

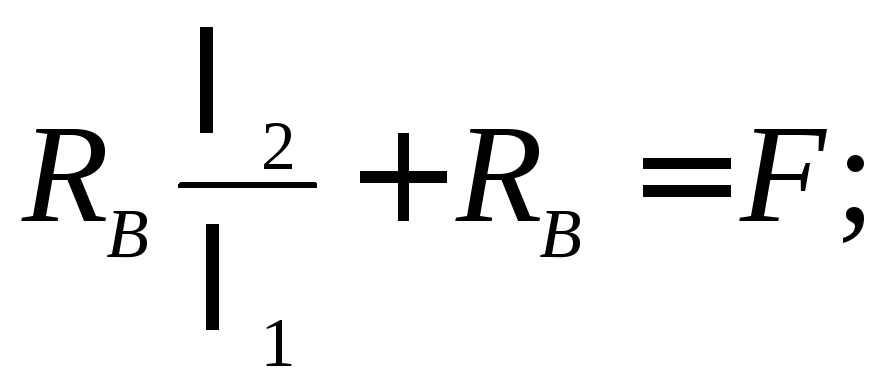
3. МЕХАНИЧЕСКИЕ ИСПЫТАНИЯ СВОЙСТВ МАТЕРИАЛОВ

3.1. Диаграмма растяжения

Для изучения свойств материалов и установления значений предельных напряжений проводят испытания образцов материалов вплоть до разрушения.

По виду деформации, испытываемой образцом, различают испытания на растяжение, сжатие, кручение и изгиб. Реже проводят испытания на сложное сопротивление.

Поскольку результаты испытаний зависят от формы образца, скорости его деформирования, температуры и других факторов, то эксперимент проводят в условиях, предусмотренных ГОСТом. Испытания проводят на специальных машинах. Наибольшее распространение имеют испытания на растяжение статической нагрузкой, т.к. они наиболее просты и в то же время во многих случаях дают возможность достаточно верно судить о поведении материала при других видах деформаций. Для испытаний на растяжение применяют цилиндрические или плоские образцы. В качестве основных используются цилиндрические образцы диаметром длиной(короткие) либо(длинные).

Целью испытаний на растяжение является определение механических характеристик материала. При испытании автоматически изображается диаграмма зависимости между растягивающим усилием F и удлинением образца .

Для того чтобы можно было сравнить результаты испытания образцов различных размеров, изготовленных из одинаковых материалов, полученную диаграмму перестраивают в другой системе координат. По оси ординат откладывают не силы, а нормальные напряжения, получаемые делением силы на первоначальную площадь поперечного сечения образца По оси абсцисс вместо абсолютных откладывают относительные удлиненияТакую диаграмму называют условной диаграммой растяжения, т.к. напряжения и относительные деформации вычисляются соответственно по отношению к первоначальной площади сечения и длине образца. Таким образом, диаграмма устанавливает связь между напряжениями и деформациями образца за всё время испытаний.

На рис. 3.1 изображена условная диаграмма растяжения для малоуглеродистой стали. Рассмотрим её характерные точки.

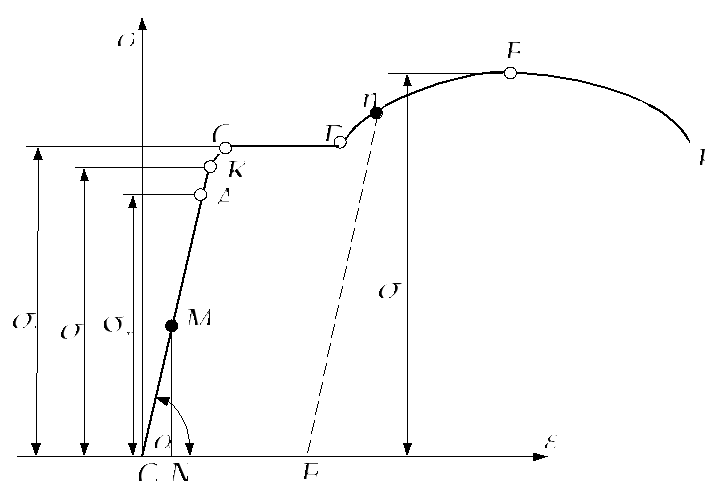
Рис. 3.1

На участке ОА до некоторого напряжения σ_пр деформации растут пропорционально напряжениям, следовательно, на этом участке сохраняет силу закон Гука. Точка А соответствует напряжению, называемому пределом пропорциональности σ_пр. Предел пропорциональности – это наибольшее напряжение, до которого деформации в материале растут пропорционально напряжениям. Если взять какое-нибудь состояние образца в пределах прямолинейного участка деформации, например М, то тангенс угла наклона линии ОА к оси абсцисс можно представить в виде

(3.1)

Модуль упругости первого рода может быть определён как тангенс угла наклона прямолинейного участка ОА к оси абсцисс.

За точкой А диаграмма становится криволинейной. Однако если величина напряжений не превысит некоторого значения , соответствующего точкеК, то материал сохраняет свои упругие свойства и при разгрузке образец восстанавливает свою форму и размеры. Это напряжение называется пределом упругости. Разница между σ_пр и на практике невелика и обычно между ними не делают различия. Например, для стали Ст3 эти величины соответственно равны 210 МПа и 220 МПа.

При дальнейшем увеличении нагрузки за пределом упругости, начиная с точки С, деформации начинают расти без увеличения напряжений. Это явление называется текучестью материала. Горизонтальный участок диаграммы CD называется площадкой текучести. Напряжение, при котором происходит рост деформации без увеличения нагрузки, называется пределом текучести и обозначается . Для стали Ст3 предел текучести равен 230 МПа. Напряжения выше предела текучести вызывают в деталях недопустимые остаточные деформации. Если от какой-нибудь точкиn диаграммы

(см. рис. 3.1), лежащей выше площадки текучести, произвести разгрузку образца, то линия разгрузки nF будет прямой, параллельной ОА. Отрезок OF представляет величину пластической деформации, которая останется в образце после разгрузки.

Ряд материалов, таких как легированные стали, не имеют ярко выраженной площадки текучести, и для них устанавливается так называемый условный предел текучести. Напряжение, при котором остаточная деформация равна 0,2 %, называется условным пределом текучести и обозначается .

После перехода площадки текучести материал снова приобретает способность сопротивляться деформированию. Диаграмма за точкой D вновь поднимается вверх, хотя и менее интенсивно, чем в зоне упругих деформаций. Точка В диаграммы соответствует наибольшему напряжению, которое называется пределом прочности или временным сопротивлением. Обозначается предел прочности или. Для стали Ст3 σ_в = 380 МПа. У высокопрочных легированных сталей достигает 1700 МПа.

После перехода предела прочности на образце появляется местное сужение – шейка. Площадь сечения шейки быстро уменьшается, вследствие чего деформация образца происходит при уменьшающихся нагрузке и соответственно напряжении. При напряжении, соответствующем точке В,

образец разрывается.

Для изготовления деталей и элементов конструкций применяют пластичные и хрупкие материалы. Под пластичностью понимают способность материала получать большие остаточные деформации без разрушения. В качестве мер пластичности в технике используют относительное остаточное удлинение образца после разрыва и относительное остаточное уменьшение площади поперечного сечения в шейке после разрыва:

(3.2)

где – длина образца после разрыва, составленного из двух частей;– длина образца до испытания;– площадь сечения в шейке;– площадь поперечного сечения образца до испытания.

Для стали Ст3 значение составляет 50…60 %.

Хрупкостью называется свойство материала разрушаться без образования заметных остаточных деформаций. Для таких материалов удлинение при разрыве составляет менее 5 %. Это свойство противоположно пластичности. Для сравнения на рис. 3.2 приведены условные диаграммы растяжения для пластичного (малоуглеродистая сталь) и хрупкого (чугун) материалов.

Рис. 3.2

Деление материалов на пластичные и хрупкие является условным, т.к. в зависимости от температуры, скорости деформирования, напряжённого состояния и других факторов пластичность изменяется. При изготовлении деталей в практике широко используется термическая обработка, которая позволяет изменять свойства материалов для улучшения эксплуатационных характеристик деталей. В частности, закалка резко повышает прочность стали и одновременно снижает её пластические свойства.