
- •Сопротивление материалов
- •2.1. Построение эпюр продольных сил
- •2.2. Определение нормальных напряжений в поперечных сечениях
- •2.3. Определение деформаций
- •2.4. Статически неопределимые задачи при осевом растяжении или
- •3.1. Диаграмма растяжения
- •3.2. Твёрдость
- •3.3. Определение допускаемых напряжений и коэффициента запаса
- •4.1. Напряжения в наклонных площадках при осевом растяжении
- •4.2. Напряжения на взаимно-перпендикулярных площадках
- •4.3. Определение напряжений в наклонных сечениях при
- •4.4. Определение главных напряжений и главных площадок
- •4.5. Обобщённый закон Гука
- •5.1. Статические моменты плоских фигур
- •5.2. Моменты инерции плоских сечений
- •5.3. Моменты инерции простых плоских сечений
- •5.4. Центробежный момент инерции
- •5.5. Изменение моментов инерции при повороте осей
- •5.6. Главные оси инерции и главные моменты инерции
- •5.7. Зависимость между моментами инерции относительно
- •5.8. Зависимость между центробежными моментами инерции
- •6.1. Определение напряжений и деформаций при сдвиге
- •6.2. Определение внутренних силовых факторов при кручении
- •6.3. Определение касательных напряжений при кручении
- •6.4. Определение деформаций при кручении стержня круглого
- •7.1. Общие понятия о деформации изгиба
- •7.2. Опоры и опорные реакции балок
- •7.3. Определение опорных реакций
- •7.4. Поперечная сила и изгибающий момент в сечении
- •7.5. Зависимость между изгибающим моментом, поперечной силой
- •7.6. Построение эпюр поперечных сил и изгибающих моментов
- •7.7. Определение нормальных напряжений при изгибе
- •7.8. Условие прочности по нормальным напряжениям
- •7.9. Касательные напряжения при изгибе балки прямоугольного
- •7.10. Аналитический способ определения деформаций при изгибе
- •7.11. Пример определения деформаций при изгибе
- •9.1. Совместное действие изгиба с кручением
- •9.2. Косой изгиб
- •9.3. Сочетание изгиба с растяжением или сжатием
- •9.4. Внецентренное растяжение или сжатие
- •10.1. Устойчивые и неустойчивые формы равновесия
- •10.2. Формула Эйлера для критической силы
- •10.3. Влияние способа закрепления концов стержней
- •10.4. Пределы применимости формулы Эйлера
- •10.5. Практические формулы расчёта на устойчивость
- •Оглавление
- •Троицкий Игорь Витальевич
9.3. Сочетание изгиба с растяжением или сжатием
До сих пор при рассмотрении изгиба балок предполагалось, что внешние силы, действующие на балку, перпендикулярны её оси. Рассмотрим более общий случай, когда изгибающая сила, действующая на балку, наклонна к её оси.
На балку,
защемлённую одним концом, действует
сила F
в плоскости продольной симметрии балки
под углом
![]() к оси балки (рис. 9.7).
к оси балки (рис. 9.7).
Разложим силу F
на две составляющие
![]() и
и![]() .
Сила
.
Сила![]() ,
перпендикулярная к оси, вызывает изгиб
балки, а сила
,
перпендикулярная к оси, вызывает изгиб
балки, а сила![]() ,
действующая вдоль оси, вызывает в балке
растяжение.
,
действующая вдоль оси, вызывает в балке
растяжение.
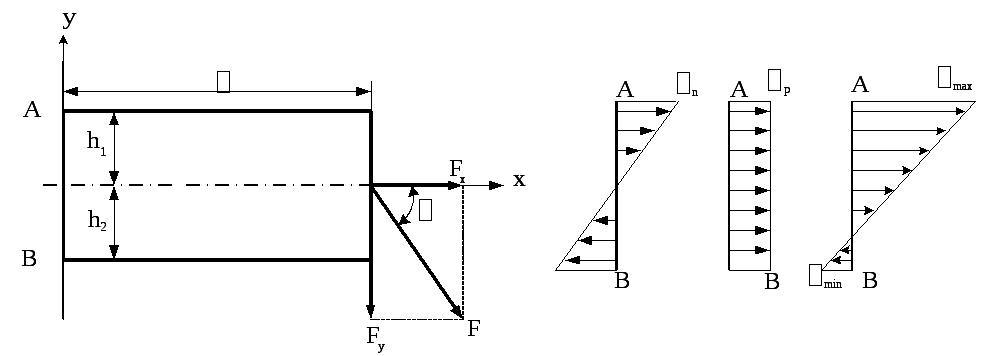
Рис. 9.7
Нормальное
напряжение, вызываемое силой
![]() ,
во всех поперечных сечениях балки
одинаково и распределено по сечению
равномерно.
,
во всех поперечных сечениях балки
одинаково и распределено по сечению
равномерно.
σр = Fx/A.
Напряжения изгиба зависят от величины момента. Наибольший изгибающий момент будет в защемлении, поэтому наиболее опасным сечением будет сечение, граничащее с защемлением. Максимальные напряжения в этом сечении:
 –напряжение
растяжения в верхних крайних волокнах;
–напряжение
растяжения в верхних крайних волокнах;
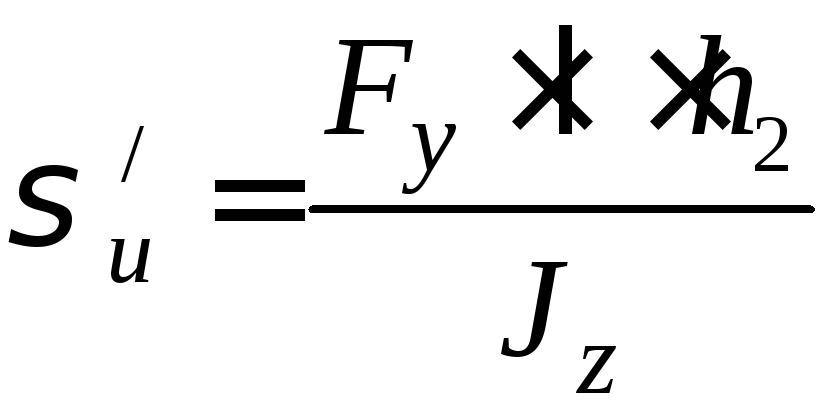 –напряжение сжатия
в нижних крайних волокнах.
–напряжение сжатия
в нижних крайних волокнах.
Суммарное напряжение в точке А:
 .
(9.15)
.
(9.15)
Для точки B:
 .
(9.16)
.
(9.16)
Напряжение
![]() если
если ;
;![]() если
если ;
;![]() при
при .
.
Таким образом,
знак
![]() зависит от соотношения напряжений
зависит от соотношения напряжений![]() и
и .
Эпюра напряжений приведена на рис. 9.7
(|
.
Эпюра напряжений приведена на рис. 9.7
(|![]() |
> σр).
|
> σр).
В частном случае,
когда
![]() ,
имеем
,
имеем
 ;
;
 .
.
Если составляющая
![]() не растягивает, а сжимает балку, тогда
не растягивает, а сжимает балку, тогда
 ;
;
 .
.
В этом случае
предполагаем, что балка настолько
жестка, что прогибы незначительны и
сила
![]() ,
сжимающая балку, всё время действует
параллельно оси балки, не вызывая её
искривления, т.е. не даёт момента
относительно нейтральной оси поперечного
сечения.
,
сжимающая балку, всё время действует
параллельно оси балки, не вызывая её
искривления, т.е. не даёт момента
относительно нейтральной оси поперечного
сечения.
9.4. Внецентренное растяжение или сжатие
Часто осевая продольная нагрузка бывает приложена не в центре тяжести поперечного сечения стержня, а с некоторым смещением относительно главных осей сечения (рис. 9.8).

Рис. 9.8
Для определения внутренних усилий применим метод сечений. В любом поперечном сечении стержня действуют продольная сила N=F и изгибающие моменты:
относительно оси z
![]() ;
;
относительно оси у:
![]() .
.
Поэтому напряжение в любой точке с координатами z и y определяется, как при осевом растяжении и изгибе в двух плоскостях (как при косом изгибе)
 . (9.17)
. (9.17)
Для сечений, имеющих выступающие угловые точки, экстремальные напряжения определяются по формуле:
 (9.18)
(9.18)
где
![]() и
и![]() – моменты сопротивления сечения
относительно осейz
и у.
– моменты сопротивления сечения
относительно осейz
и у.
![]() и
и ![]() .
.
В сечении на рис. 9.8 наибольшие напряжения будут в точке Е, т.к. здесь суммируются растягивающие напряжения от центрального растяжения и растягивающие напряжения от изгиба в двух плоскостях:

Наименьшее напряжение (в алгебраическом смысле) будут в точке D:

при этом они могут быть как растягивающие, так и сжимающие.
Условие прочности по растягивающим напряжениям имеет вид
 .
(9.19)
.
(9.19)
Если точка
приложения силы находится на одной из
главных осей сечения, например на оси
у,
то
![]() и формула упрощается:
и формула упрощается:
![]()
При произвольной форме поперечного сечения для определения положения опасных точек необходимо найти положение нулевой линии. Уравнение нулевой линии получим, приравняв нулю выражение
![]() ,
(9.20)
,
(9.20)
где
![]() и
и![]() – текущие координаты нулевой линии.
– текущие координаты нулевой линии.
Введём обозначения:
![]() ;
;![]()
Величины
 и
и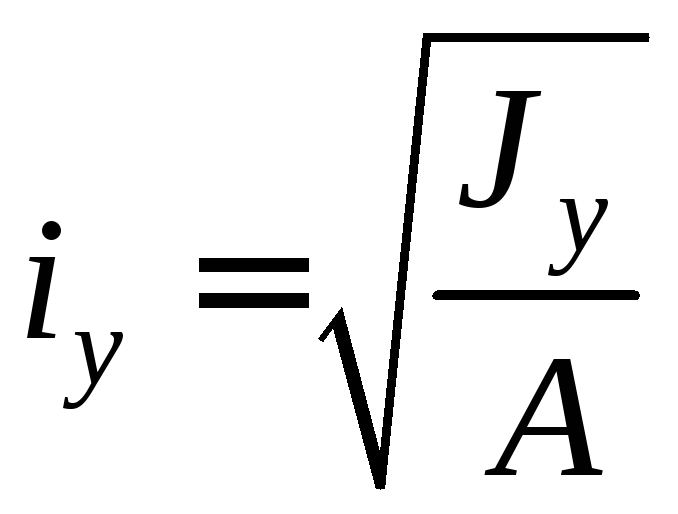 называются радиусами инерции сечения
относительно осейz
и у
и относятся к категории геометрических
характеристик сечений. Размерность
радиуса инерции – единица длины.
Представим формулу (9.20) в виде
называются радиусами инерции сечения
относительно осейz
и у
и относятся к категории геометрических
характеристик сечений. Размерность
радиуса инерции – единица длины.
Представим формулу (9.20) в виде
![]() .
.
Так как
![]() то
то
![]() (9.21)
(9.21)
Это и есть уравнение нулевой линии. Его можно представить в виде уравнения прямой в отрезках:
![]()
где

представляют собой отрезки, отсекаемые нулевой линией на осях z и у.
Поскольку радиус
инерции всегда положителен, то величины
а
и
![]() ,
а такжеb
и
,
а такжеb
и
![]() имеют разные знаки.
имеют разные знаки.
Определив положение нулевой линии, легко построить эпюру параллельных положений. Для этого проводим линию I-I (ось эпюры) перпендикулярно нулевой линии. Сносим на эту ось крайние точки сечения D и E, опуская на линию I-I перпендикулярны из этих точек.
Для построения
эпюры имеем две точки: точку на нулевой
линии, где
![]() ,
и точку L,
полученную из условия, что отрезок ML
в определённом масштабе должен обозначать
напряжение в центре тяжести сечения.
Поскольку в центре тяжести сечения
z=y=0,
то по формуле (9.17) получаем, что это
напряжение
,
и точку L,
полученную из условия, что отрезок ML
в определённом масштабе должен обозначать
напряжение в центре тяжести сечения.
Поскольку в центре тяжести сечения
z=y=0,
то по формуле (9.17) получаем, что это
напряжение
![]()
10. РАСЧЕТ СЖАТЫХ СТЕРЖНЕЙ НА УСТОЙЧИВОСТЬ
