9.2. Косой изгиб

До сих пор мы рассматривали изгиб, когда плоскость действия нагрузок совпадала с продольной плоскостью симметрии балки или с одной из главных плоскостей. Деформация изгиба при этом происходила в плоскости действия моментов, а нейтральная ось совпадала с главной осью инерции поперечного сечения и была перпендикулярна к плоскости действия момента.

Однако встречаются случаи, когда плоскость действия моментов не совпадает ни с одной из главных плоскостей балки. Такой изгиб называется косым изгибом.

Рассмотрим пример косого изгиба.

Балка прямоугольного сечения (рис. 9.4), защемлённая одним концом, изгибается силой F, перпендикулярной к оси балки на свободном конце и составляющей угол с главной плоскостьюху. Поскольку плоскость действия изгибающих моментов не совпадает ни с одной из главных плоскостей балки, мы здесь имеем случай косого изгиба.

Рис. 9.4

Абсолютное значение изгибающего момента в каком-либо сечении m-n, отстоящем на расстоянии х от защемления, определяется выражением

Разложим силу F на две составляющие по главным осям сечения у и z. Тогда абсолютные значения составляющих моментов можно представить в виде

Моменты идействуют в главных плоскостях балки. Напряжения от каждого из этих моментов, взятых в отдельности, мы определить сможем. Пользуясь законом независимости действия сил, можно найти напряжения, получающиеся при одновременном действии моментови.

Таким образом, случай косого изгиба всегда можно свести к двум плоским изгибам.

Под действием одного только момента нейтральной осью будет осьz, и нормальное напряжение для какой-либо точки N с координатами у, z, взятой в первом квадранте сечения m-n (рис. 9.5), определится по формуле

.

Напряжение в той же точке от действия одного лишь момента равно

.

Рис. 9.5

При одновременном действии двух моментов инапряжение в любой точке сечения будет равно алгебраической сумме напряженийи, т.е.

. (9.12)

В эту формулу координаты у, z точек сечения и изгибающие моменты подставляются со своими знаками.

Если момент вызывает растяжение в I–й четверти, где z > 0 и y > 0, то ему приписывается знак «+», если сжатие – то «–».

В точке А .

В точке В .

.

В точке С

.

В точке D

.

Наибольшее суммарное напряжение в данном случае будет в точках

B и D; в точке B (y>0; z>0) – напряжение растяжения, в точке D (y<0; z<0) – напряжение сжатия. Абсолютные значения этих напряжений будут одинаковы.

Уравнение нейтральной линии получим, приравняв нулю правую часть формулы (9.12):

, или что то же самое:

, откуда

;

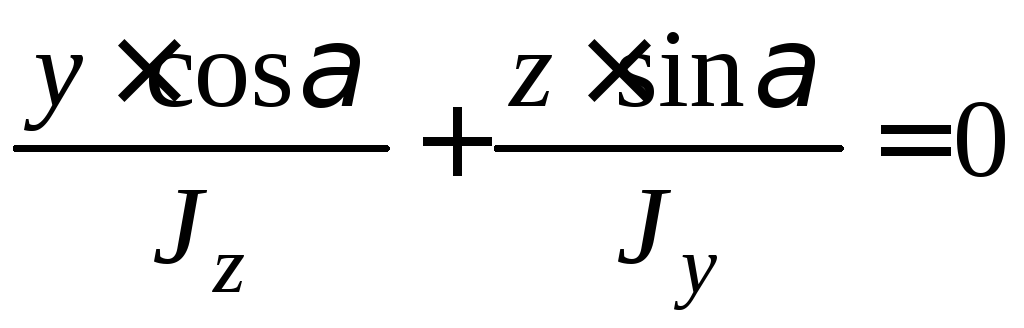. (9.13)

Этому уравнению прямой линии удовлетворяют значения у=0 и z=0. Следовательно, нейтральная линия проходит через центр тяжести поперечного сечения.

Определим из (9.13) отношение у/z и найдём тем самым tg угла , составляемого нейтральной осью с положительным направлением осиz

(рис. 9.6).

. (9.14)

Из формулы (9.14) видно, что для сечений, у которых (например, квадрат, круг,), т.е. нейтральная линия всегда будет перпендикулярна к плоскости действия изгибающего момента, в которой и происходит деформация изгиба.

Рис. 9.6

Таким образом, балки, у которых все центральные оси поперечных сечений являются главными (правильные фигуры), не могут иметь косого изгиба.

В тех же случаях, когда ,и, нейтральная линия не будет перпендикулярна к плоскости изгибающего момента.