9.1. Совместное действие изгиба с кручением

На практике кручение часто сопровождается деформацией изгиба. С таким сложным видом деформации приходится иметь дело при расчёте валов передач, когда силы, действующие на вал, не проходят через его ось.

Ведущее зубчатое колесо передаёт окружное усилие на расстояниеd/2 от центра колеса, т.е. от центра вала, на котором это колесо расположено

(рис. 9.1).

Рис. 9.1

Перенесём силу в центр вала. Чтобы система сил была эквивалентной, приложим вторую силу, направленную противоположно.

Получим в результате пару сил с моментом, равным , скручивающую вал, и силу, которая вал изгибает.

Следовательно, в материале вала возникают нормальные напряжения от изгиба и касательные от кручения, которые определяются по известным зависимостям

;

Наибольшее напряжение от изгиба и от кручения возникают на поверхности вала (рис. 9.2). Каждое из них, взятое в отдельности, может быть меньше допускаемого для соответствующего вида деформации. Однако их одновременное действие может привести к разрушению вала.

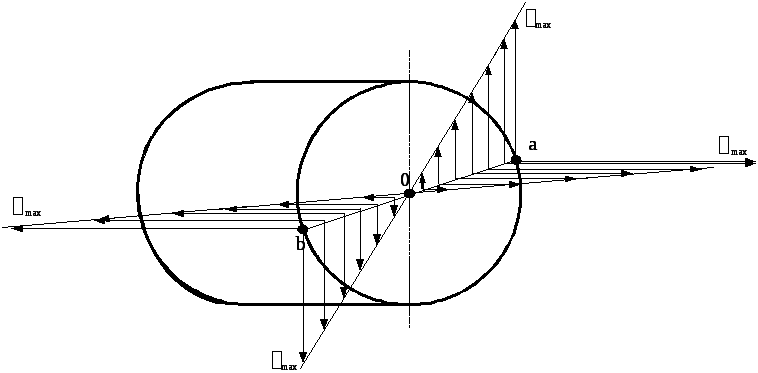
Рис. 9.2

Для оценки одновременного действия нормального напряжения от изгиба и касательногокручения выделим в наиболее опасном сечении у наиболее опасной точкиа или b элемент материала (рис. 9.3, а). По четырём граням этого элемента действуют касательные напряжения, а по двум – ещё и нормальные , следовательно, мы имеем случай плоского напряжённого состояния. Для определения главных напряжения (рис. 9.3,б) при плоском напряжённом состоянии воспользуемся известными формулами:

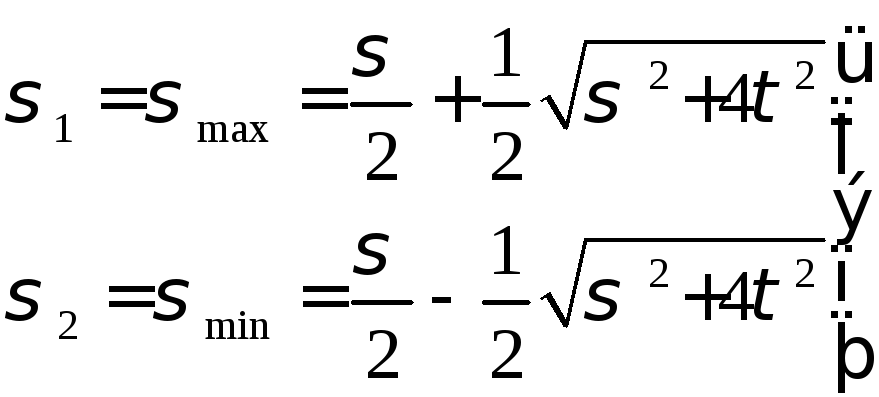(9.1)

Рис. 9.3

В соответствии с третьей теорией прочности подставим в формулу (8.4) значения главных напряжений ииз (9.1) и получим следующую зависимость, выражающую условие прочности:

. (9.2)

Здесь игдеd – диаметр вала в расчётном сечении. Подставим значения ив формулу (9.2):

. (9.3)

Обозначим через– приведённый момент. Тогда условие прочности по третьей теории можно записать в виде

(9.4)

Из (9.4) получаем зависимость для определения диаметра вала по третьей теории прочности:

. (9.5)

В случае, если вал испытывает изгиб в двух взаимно перпендикулярных плоскостях, то изгибающий момент определяем по формуле

. (9.6)

По четвёртой теории условие прочности для плоского напряжённого состояния имеет вид

. (9.7)

Подставляя значения главных напряжений и, выраженных через напряжения от изгиба и от кручения (формулы (9.1)), получим

. (9.8)

Следовательно,

. (9.9)

Таким образом, приведённый момент по четвёртой теории прочности определяется по формуле

. (9.10)

Диаметр вала определяют по формуле (9.5), подставляя полученное значение по четвёртой теории прочности.

Расчёт по третьей теории рекомендуется применять при расчёте нереверсивных валов, по четвёртой – для реверсивных.

Допускаемое напряжение принимают для валов, выполненных из углеродистой стали, в пределах 60 МПа либо определяют в зависимости от предела прочности по формуле

(9.11)

Оценка прочности и определение диаметра вала по четвёртой (энергетической) теории прочности производится по формулам (9.4) и (9.5), в которые должен быть подставлен приведённый момент, рассчитанный по выражению (9.10).

Отметим, что формула (9.5) для третьей и четвёртой теорий прочности даёт практически один и тот же результат, так как полученный при расчёте диаметр вала должен быть округлён до стандартного значения в соответствии с нормальным рядом линейных размеров по ГОСТ 6636-69.