7.8. Условие прочности по нормальным напряжениям

Согласно уравнению (7.9) наибольшие нормальные напряжения, могущие привести к разрушению, возникают в волокнах, наиболее удалённых от нейтральной оси. Так как при прочностных расчётах определяются максимальные напряжения, то в формуле (7.9) вместо текущего значения у подставляют расстояние от нейтральной оси до наиболее удалённых волокон.

Наибольшие напряжения растяжения

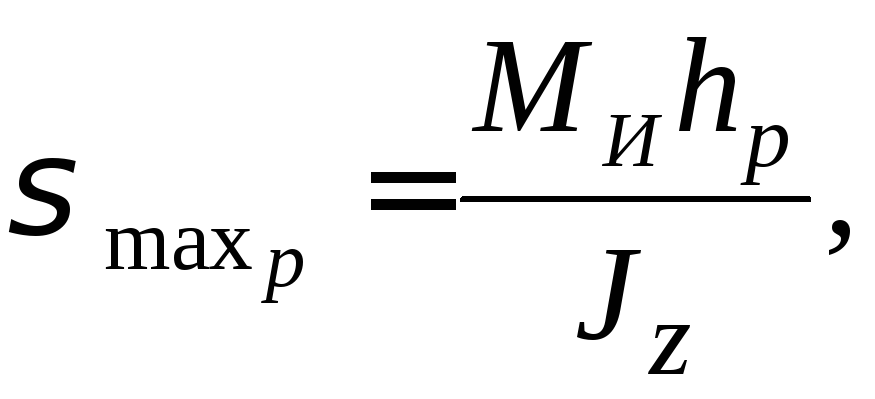
где – расстояние от нейтральной оси до наиболее удалённых волокон в растянутой зоне.

Наибольшие напряжения сжатия

где – расстояние от нейтральной оси до наиболее удалённых сжатых волокон.

Таким образом, при несимметричном профиле, когда не равнои если материал балки по – разному реагирует на растяжение и сжатие, то условие прочности запишется следующим образом:

(7.10) где и– допускаемые напряжения при растяжении и сжатии соответственно.

Если профиль балки симметричный, т.е. , а также в случае, когда материал одинаково сопротивляется и растяжению и сжатию, то достаточно определить только максимальное напряжение для тех волокон, которые наиболее удалены от нейтральной оси:

Если величина изгибающего момента по длине бруса меняется, то для определения максимальных напряжений необходимо брать то сечение, в котором действует максимальный момент. Такое сечение бруса называется опасным сечением.

Отношение момента инерции сечения относительно нейтральной оси к расстояниюнаиболее удалённого от этой оси волокна называется моментом сопротивления сечения при изгибе и обозначаетсяили в общем виде:

(7.11)

Таким образом, в случае симметричного относительно нейтральной оси сечения балки, т.е. при или при одинаковых допускаемых напряжениях на растяжение и сжатие, вместо двух формул (7.10) получим одну, выражающую условие прочности по нормальным напряжениям при изгибе:

(7.12)

Для стандартных профилей проката, таких как швеллер, двутавр, уголок, значения осевых моментов сопротивления приведены в таблицах сортамента.

Для прямоугольного сечения

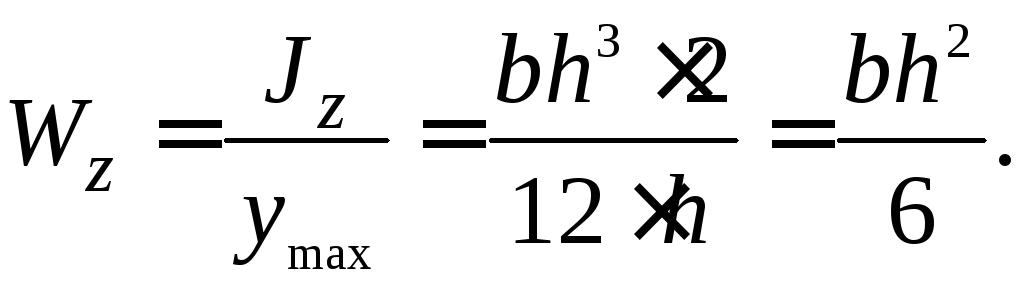(7.13)

Для квадратного сечения со стороной а

(7.14)

Для круглого сечения

(7.15)

Для кольцевого сечения с наружным диаметром D и внутренним d

(7.16)

где

Используя уравнение (7.12), можно подобрать сечение профиля, исходя из условия прочности по нормальным напряжениям. Определим требуемый осевой момент сопротивления

(7.17)

Затем по таблицам стандартных прокатных профилей или в соответствии с формулами (7.13)-(7.16) в зависимости от задания выбираем или рассчитываем сечение.

7.9. Касательные напряжения при изгибе балки прямоугольного

сечения. Формула Д.И. Журавского

В общем случае поперечного изгиба в поперечных сечениях балки действуют изгибающие моменты, вызывающие нормальные напряжения и поперечные силы. Поперечная сила стремится сдвинуть одну часть балки относительно другой в направлении, перпендикулярном оси балки. Поэтому поперечная сила вызывает в плоскости поперечного сечения балки касательные напряжения. В силу закона парности касательных напряжений в балке появляются касательные напряжения, действующие параллельно нейтральной плоскости, которые стремятся сдвинуть горизонтальные слои балки друг относительно друга.

Рассмотрим, каким образом можно определить величину этих касательных напряжений и закон их распределения по высоте балки. При этом рассмотрим простейший случай, когда балка имеет прямоугольное сечение. В случае прямоугольного сечения можно предположить, что касательные напряжения в поперечном сечении параллельны поперечной силе Q и что величина их не меняется по ширине балки, т.е. вдоль нейтральной оси z-z. Опыт показывает, что такое предположение даёт весьма небольшую ошибку.

Возьмём балку прямоугольного сечения со сторонами изгибаемую силойF. Проведём слева от силы F два сечения 1-1 и 2-2, отстоящих на dx, и продольное сечение ab, параллельное нейтральному слою, на расстоянии от него (рис. 7.17).

Рис. 7.17

Этими тремя сечениями на балке вырежется бесконечно узкий параллелепипед mabn с размерами dx, h/2 – иb. Обозначим изгибающий момент в сечении 1-1 через М, в сечении 2-2 – через . Поперечные сечения 1-1 и 2-2 проведены на левом участке балки, где изгибающие моменты положительны. Положительны и поперечные силы. ПоэтомуилиdM >0.

Рассмотрим условия равновесия параллелепипеда mabn, мысленно выделив его из балки. Действие на него отброшенной части балки заменим внутренними усилиями. По боковым граням параллелепипеда будут действовать сжимающие нормальные усилия и, вызванные изгибающими моментами, причём, т.к.. Кроме того, по боковым граням будут действовать касательные усилия, вызванные поперечными силами. Равнодействующую этих усилий обозначим черезТ.

Вследствие того, что , параллелепипед должен передвинуться влево. Этому препятствуют касательные усилия, появляющиеся на граниab. Результирующую этих усилий обозначим через T ^/.

Рис. 7.18

Элементарное усилие, действующее на бесконечно малую площадку dA левой грани параллелепипеда, находящегося на расстоянии у от нейтральной оси (рис. 7.19), можно представить в виде

,

где – момент инерции всего сечения относительно нейтральной оси.

Нормальное усилие, действующее на всю левую грань:

,

где – площадь части поперечного сечения отдо;

–величина постоянная, т.к. М=const и y=const.

Поэтому .

Рис. 7.19

Аналогично: нормальное усилие, действующее на правую грань параллелепипеда .

Величина результирующей Т касательных усилий, действующих на нижней грани параллелепипеда, если их считать равномерно распределёнными:

. (7.18)

Спроектируем все силы на ось х: Подставим в выражение (7.18) значенияи:

,

или ,

откуда . (7.19)

Интеграл представляет статический момент площади отсечённой части сечения относительно нейтральной оси. Обозначим его через.

Величина равнаQ, т.е. поперечной силе, поэтому выражение (7.19) окончательно можно записать в следующем виде:

(7.20)

Таким образом, касательные напряжения в продольном слое балки равны произведению поперечной силы Q в рассматриваемом сечении на статический момент относительно центральной оси части поперечного сечения, лежащей выше рассматриваемого уровняделённому на момент инерциивсего сечения относительно нейтральной оси и на ширинупоперечного сечения балки.

Для данного сечения величины Q и постоянны. Поэтому касательные напряжения изменяются прямо пропорционально отношению. В самых верхних и нижних продольных сечениях балки, там где нормальные напряжения от изгибающих моментов имеют наибольшие значения, касательные напряжения равны0, т.к. для них Для сечений, у которых ширинаb=const, наибольшие касательные напряжения будут в нейтральном слое, т.к. для него В общем случаеиb величины переменные, поэтому предсказать заранее, где обнаружатся максимальные касательные напряжения, нельзя. Можно только сказать, что они будут максимальными для тех слоев, где имеет максимальное значение.

Вследствие закона парности касательных напряжений (касательные напряжения в двух взаимно перпендикулярных плоскостях равны между собой по абсолютной величине и противоположны по знаку) формула (7.20) определяет и величину касательных напряжений в поперечных сечениях балки. Следовательно, в поперечных сечениях балки касательные напряжения распределяются неравномерно.

Касательные напряжения вызывают деформацию сдвига балки, которая не отражается на распределении нормальных напряжений, определяемых формулой .

Вследствие деформации сдвига плоские до изгиба поперечные сечения не остаются плоскими, как при чистом изгибе, а искривляются. Рис. 7.20 показывает искривление поперечных сечений. Там, где достигают максимальных значений, происходит и наибольший сдвиг; волокна, наиболее

Рис. 7.20

удаленные от нейтрального слоя, не имеют касательных напряжений, поэтому там сдвиг отсутствует и кривые mn остаются перпендикулярными к поверхностям балки.

Рассмотрим распределение касательных напряжений в балке прямоугольного сечения (рис. 7.21).

Рис. 7.21

Касательные напряжения по линии ab, отстоящей на расстоянии у от нейтрального слоя, можно рассчитать по формуле (7.20).

Для рассматриваемого сечения балки Q, J_z, b, – постоянные величины.

Статический момент заштрихованного прямоугольника aABb:

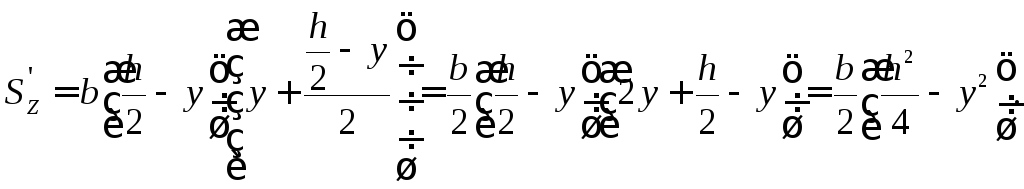
Момент инерции всего сечения относительно центральной оси:

.

Подставим значения ив формулу (7.20).

(7.21)

принимает наибольшее значение, когда у=0, т.е. на нейтральной оси.

.

Величина – среднее касательное напряжение. Следовательно,для прямоугольного сечения в 1,5 раз больше среднего, полученного при равномерном распределениипо сечению.

Формула (7.21) показывает, что касательные напряжения изменяются по сечению по закону параболы. Для Эпюра касательных напряжений симметрична относительно нейтральной оси, т.ку входит в формулу в квадрате, поэтому знак при у на величину не влияет. Следовательно, волокна, симметрично удалённые от нейтральной оси в прямоугольном сечении, имеют одинаковые касательные напряжения.

Формула для определения касательных напряжений была выведена в 1855 году выдающимся русским инженером Д.И. Журавским и поэтому носит его имя.