7.5. Зависимость между изгибающим моментом, поперечной силой

и интенсивностью распределённой нагрузки

Рассмотрим балку, нагруженную силами ,,. Опорные реакции – и(рис. 7.11). Запишем момент в сеченииот сил, лежащих левее сечения:

Поперечная сила в этом сечении равна алгебраической сумме внешних сил, приложенных слева от сечения

Индекс «х» у изгибающего момента и поперечной силы означает, что они являются функциями абсциссы x.

Определим значение момента в сечении расположенного на расстоянииdx от первого сечения:

.

Приращение момента

т.е. откуда

. (7.3)

Поперечная сила в сечении равна первой производной от изгибающего момента по абсциссе сечения.

Рис. 7.11

Этот вывод справедлив и при наличии равномерно распределённой нагрузки q.

Рассмотрим балку, нагруженную равномерно распределённой нагрузкой q и силами F₁ и F₂ (рис. 7.12). Если в сечении n-n поперечная сила равна , то в сечении, расположенном на расстоянииот рассматриваемого, поперечная сила будет равнагдеСледовательно,

(7.4)

т.е. производная от поперечной силы по абсциссе сечения балки равна интенсивности распределенной нагрузки.

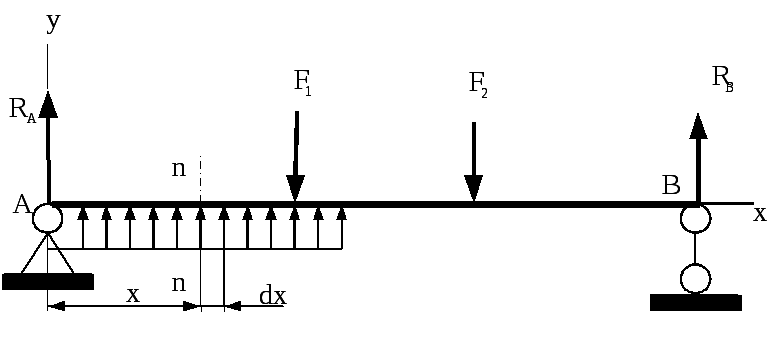
Рис. 7.12

Возьмём производную от обеих частей равенства (7.3) и получим

, (7.5)

т.е. вторая производная от изгибающего момента по абсциссе сечения равна интенсивности распределённой нагрузки.

Зависимости (7.3) и (7.5) выведены русским учёным Д.И. Журавским и используются при построении эпюр поперечных сил и изгибающих моментов.

7.6. Построение эпюр поперечных сил и изгибающих моментов

Нормальные и касательные напряжения, возникающие в поперечных сечениях балки, зависят от изгибающих моментов и поперечных сил. Для определения опасных сечений и наглядного представления о характере измененияипо длине балки строят графики, которые называются эпюрами изгибающих моментов и поперечных сил. Чтобы усвоить технику их построения, рассмотримпример.

1. Построение эпюридля балки, представленной на рис. 7.13,а.

Решение

Определение опорных реакций

.

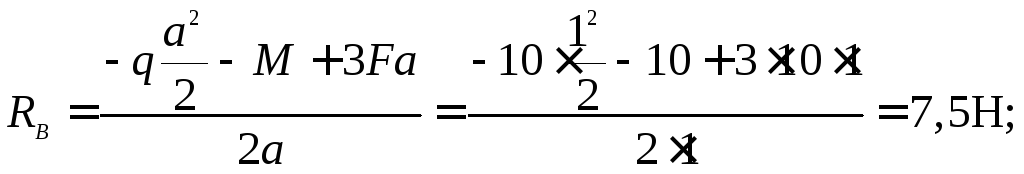
Проверка:

2. Построение эпюры поперечных сил «Q» (рис. 7.13, б). Характерными сечениями разбиваем балку на четыре участка. Сечения проводим по краям балки, а также через точки приложения сосредоточенных сил и моментов, а также в начале и конце участков с распределённой нагрузкой. Поперечную силу в пределах каждого участка будем записывать в виде уравнения, аргументом которого является переменная координата х. Поперечную силу находим в соответствии с правилом как алгебраическую сумму внешних сил, действующих слева от рассматриваемого сечения. Индекс у поперечной силы обозначает номер участка.

это уравнение прямой линии, которую можно построить по двум точкам. Определяем значение Q в начале и конце участка.

. В любом сечении участка АС поперечная сила имеет одно и то же значение, эпюра будет изображаться линией, параллельной базовой оси.

Характер эпюры тот же, что и на участке АС.

Для определения Q на участке BD удобнее отбросить левую часть и рассмотреть оставшуюся правую.

Проводим базовую ось параллельно оси балки и в масштабе строим эпюру поперечных сил на каждом участке в соответствии с уравнениями

(рис. 7.13, б).

3. Построение эпюры изгибающих моментов М_И (рис. 7.13,в). Изгибающие моменты также определяются по участкам и записываются в виде уравнений, в которых независимой переменной является координата х:

Уравнение изгибающих моментов на участке ОА является уравнением второго порядка. Для построения эпюры необходимо определить моменты трёх или более точек. Определим в начале, конце и в середине первого участка:

; .

Изгибающий момент на втором участке АС определим как алгебраическую сумму моментов внешних сил слева от сечения с координатой :

.

Получили уравнение прямой линии, которую можно построить по двум точкам, соответствующим двум значениям изгибающего момента. Находим эти значения в начале и конце участка АС:

;

.

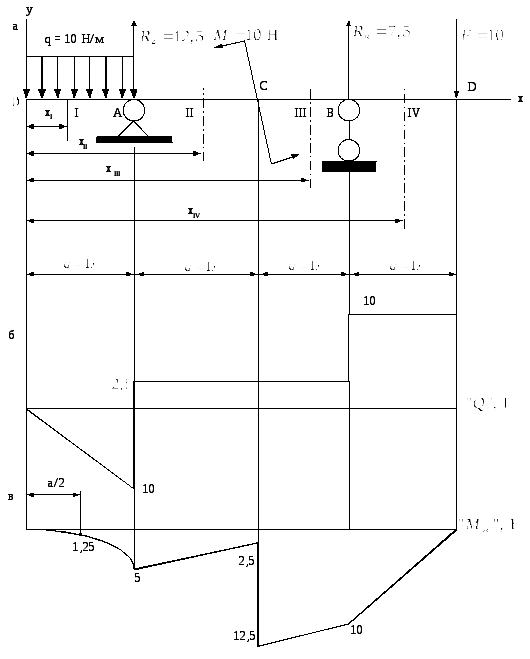
Рис. 7.13

Уравнение моментов для участка CD также запишем, суммируя моменты внешних сил, расположенных слева от сечения :

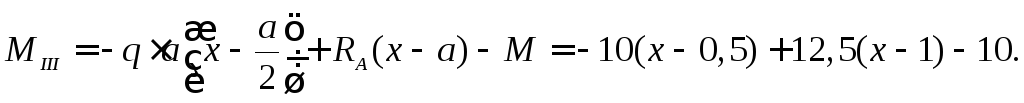
Определим значения изгибающих моментов на границах участка CB:

;

.

Для определения изгибающих моментов на четвёртом участке удобнее отбросить левую часть балки, так как к ней приложено большее число внешних сил:

Значения моментов на границах участка:

; .

Строим в масштабе эпюру «М_И» на каждом участке в соответствии с полученными уравнениями (см. рис. 7.13).

Анализируя эпюры «Q» и «М_И», можно отметить следующие зависимости между характером эпюр и нагрузок:

1) на участке с равномерно распределённой нагрузкой эпюра поперечных сил очерчивается наклонной прямой линией, а эпюра изгибающих моментов имеет криволинейное очертание – квадратичную параболу;

2) между точками приложения сосредоточенных сил поперечная сила постоянна, а эпюра моментов очерчивается наклонной прямой линией;

3) эпюра поперечных сил скачкообразно изменяется в местах приложения внешних сил, при этом величина скачка равна приложенной сосредоточенной силе;

4) сосредоточенный момент не влияет на характер эпюры поперечных сил, а на эпюре изгибающих моментов в этом сечении имеется скачок, величина которого равна приложенному внешнему моменту;

5) поперечная сила Q положительна на участках балки, где эпюра восходящая, если смотреть слева направо, и отрицательна на тех участках, где эпюранисходящая;

6) поскольку то изгибающий момент достигает экстремума (максимума или минимума) в тех сечениях, где поперечная сила равна нулю, т.е. эпюраQ пересекает базовую ось.

Перечисленные зависимости используются для контроля правильности построения эпюр внутренних силовых факторов при деформации изгиба.