7.3. Определение опорных реакций

В случае действия на балку плоской системы сил можно записать три уравнения равновесия:

откуда следует: для равновесия балки необходимо, чтобы суммы проекций всех сил, приложенных к балке, включая реакции опор на оси x и y, и сумма моментов всех сил относительно любого полюса в плоскости действия сил были равны нулю.

Если опорные реакции балок могут быть найдены из уравнений статики, то балки называют статистически определимыми. Они могут быть только двух видов:

1) балка с одним жестко защемлённым и одним свободным концом (консоль) (рис. 7.5, а);

2) балка с одной шарнирно-неподвижной и другой шарнирно-подвижной опорой (рис. 7.5, б, в). Балка, изображённая на рис. 7.5, б называется простой, а балка на рис. 7.5, в – консольной, так как имеет свешивающиеся с опор концы, которые называются консолями.

Рис. 7.5

Пример 1

Определить опорные реакции консольной балки (рис. 7.6).

Решение. Реакцию заделки представляем в виде двух составляющих – вертикальной и горизонтальной– и реактивного момента; при этом направления сил вдоль осей и направление момента принимаем произвольно. Условимся здесь и в дальнейшем осьx направлять вправо, а ось у – вверх.

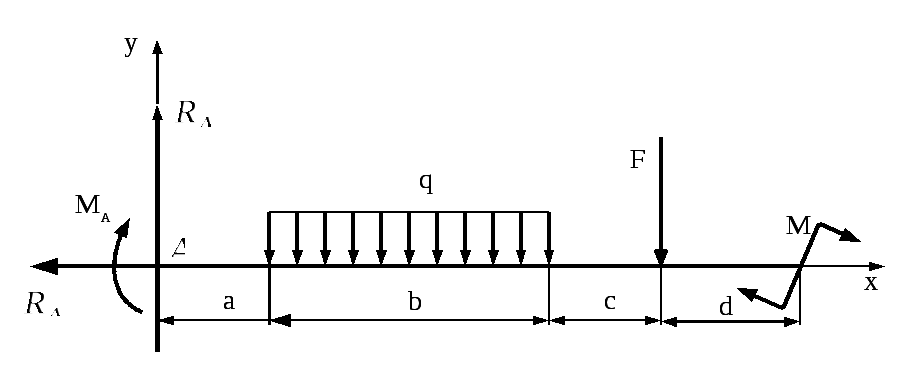
Рис. 7.6

Составляем уравнение равновесия:

1) Сумма проекций всех сил на горизонтальную ось x равна нулю: Из этого уравнения получаем, что, т.е. при отсутствии горизонтальной нагрузки горизонтальная составляющая реакции равна нулю;

2) Сумма проекций всех сил на вертикальную ось у равна нулю: Равномерно распределённую нагрузку интенсивностьюзаменяем её равнодействующейприложенной в середине участка:

откуда

3) Сумма моментов всех сил относительного любого центра равна нулю. За центр примем точку .

откуда

.

Реактивный момент получился со знаком минус, следовательно, его направление необходимо заменить на противоположное (против направления вращения часовой стрелки).

Пример 2

Определить опорные реакции двухопорной одноконсольной балки

(рис. 7.7).

Решение. Поскольку горизонтальная нагрузка отсутствует, то

Рис. 7.7

В качестве проверочного воспользуемся уравнением проекций всех сил на вертикальную ось

7.4. Поперечная сила и изгибающий момент в сечении

При плоском поперечном изгибе в любых поперечных сечениях балки возникают два внутренних силовых фактора – поперечная сила и изгибающий момент. Для их определения, как и при других видах деформаций, применим универсальный метод, который называется методом сечений.

Мысленно рассечём балку по сечению , находящемся на расстоянииот левой опоры(рис. 7.8,а). Правую часть балки отбросим и рассмотрим равновесие оставшейся левой части (рис. 7.8, б ). Для того чтобы она находилась в равновесии, в сечении должны участвовать поперечная сила и изгибающий момент, представляющие собой действие отброшенной части на оставшуюся. Для определения изапишем два уравнения равновесия:стоящего на расстоянии !!!! !!!!! х видах деформаций применим универсальный метод, который называется методом сечений.

ила !!!!

1) ;, откуда

; (7.1)

2) ;, откуда

. (7.2)

Рис. 7.8

Из (7.1) и (7.2) сформулируем правила определения Q и M_И .

Результирующая внутренних сил, приложенная в сечении оставшейся части балки, численно равна алгебраической сумме внешних сил, действующих по одну сторону от сечения, называется поперечной силой и обозначается Q.

Момент пары внутренних сил, приложенный к оставшейся части балки, численно равный алгебраической сумме моментов внешних сил, действующих по одну сторону от сечения, называется изгибающим моментом и обозначается M_И.

Если вместо левой части балки рассмотреть правую, то изгибающий момент и поперечная сила в сечении будут иметь те же значения, но иметь противоположные знаки.

Для того чтобы изгибающий момент и поперечная сила в одном и том же сечении имели один знак независимо от того, к какой части они приложены, введём следующие правила знаков.

Поперечная сила в сечении балки (рис. 7.9,а) считается положительной, если равнодействующая внешних сил слева от сечения направлена снизу вверх, а справа от сечения – сверху вниз.

В противоположном случае поперечная сила Q в сечении n-n будет считаться отрицательной (рис. 7.9, б).

Рис. 7.9

Изгибающий момент в сечении m-m (рис. 7.10, а) считается положительным, если равнодействующий момент внешних сил слева от сечения направлен по часовой стрелке, а справа от сечения – против. При направлении равнодействующих внешних моментов справа и слева от рассматриваемого сечения в другом направлении момент в сечении считается отрицательным (рис. 7.10, б).

Рис. 7.10

Из рис. 7.10 следует, что изгибающий момент считается положительным, если в рассматриваемом сечении балка изгибается выпуклостью вниз, отрицательным – если выпуклостью вверх. Волокна балок, расположенные в вогнутой части, испытывают сжатие, а в выпуклой – растяжение. При построении эпюр изгибающих моментов положительные ординаты откладывают вверх от базовой оси, таким образом, эпюра будет построена со стороны сжатых волокон балки.