7.1. Общие понятия о деформации изгиба
Рассмотрим прямолинейный брус с продольной осью симметрии, нагруженный уравновешенной системой сил, линии действия которых лежат в плоскости симметрии и перпендикулярны оси бруса (рис. 7.1). Брус под действием этих сил изогнётся, а его продольная ось искривится. Такой вид деформации называется изгибом, а брусья, работающие на изгиб, – балками.
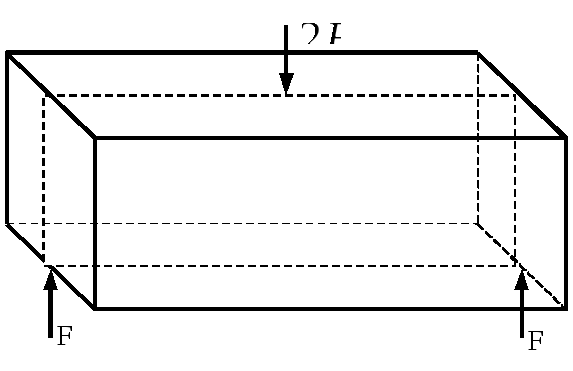
Рис. 7.1
Деформация изгиба бруса произойдёт в плоскости действия сил (силовой плоскости), вследствие чего такой изгиб называется плоским.
При изгибе в поперечных сечениях бруса возникают внутренние моменты сил упругости, плоскость действия которых перпендикулярна плоскости поперечного сечения бруса. Эти внутренние моменты называются изгибающими моментами в сечении или просто изгибающими моментами. Если изгибающий момент является единственным внутренним усилием в сечении, то такой изгиб называют чистым. Чистый изгиб возникает под действием двух равных и противоположно направленных моментов.
В случае, когда в сечениях бруса наряду с изгибающим моментом возникает также и поперечная сила, изгиб носит название поперечного.
При плоском поперечном изгибе ось балки после деформации остаётся в плоскости действия внешних сил.
7.2. Опоры и опорные реакции балок
Балки служат для передачи действующих на них внешних сил (нагрузок)
на опоры, на которых они установлены. В опорах возникают реакции, т.е. силы действия опор на рассматриваемую балку. Под действием внешних нагрузок и реакций опор балка находится в равновесии. Решение всех задач, связанных с деформацией изгиба, следует начинать с определения опорных реакций. В зависимости от числа и устройства опор балки число реакций, подлежащих определению, будет различно.
Опоры балок по их устройству подразделяются на три основных типа.
1.
Шарнирно-неподвижная
опора (рис.
7.2, а).
Конец балки
опирается на шарнир, который расположен
на неподвижной подушке. Такая опора
допускает поворот конца балки, но не
даёт ему возможности перемещаться в
каком – либо направлении. Реакция лежит
в плоскости, перпендикулярной оси
шарнира, и проходит через его центр.
Обычно эту реакцию раскладывают на две
составляющие – вертикальную
и горизонтальную
(рис.
7.2, б).
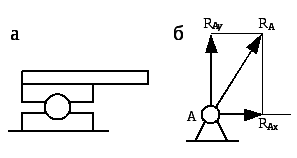
Рис. 7.2
2. Шарнирно-подвижная опора (рис. 7.3, а). Эта опора отличается от предыдущей тем, что у неё опорная подушка поставлена на катки, которые дают ей возможность передвигаться вместе с концом балки по направляющей. Таким образом, шарнирно-подвижная опора даёт возможность концу балки поворачиваться вокруг оси шарнира и перемещаться вдоль плоскости качения и накладывает на конец балки одну связь – не даёт возможности перемещаться в направлении, перпендикулярном направляющей (плоскости качения). Следовательно, такая опора даёт лишь одну составляющую реакции, неизвестную по величине и известную по направлению. Реакция проходит через центр шарнира и направлена перпендикулярно направляющей. В дальнейшем шарнирно – подвижную опору будем изображать, как показано на рис. 7.3, б.
Рис. 7.3
3.
Жёсткая
заделка, или защемление
(рис. 7.4).
Такое устройство опоры не допускает ни
угловых, ни линейных перемещений
защемлённого конца балки. В жёсткой
заделке возникают реакция, неизвестная
по величине и направлению, и реактивный
момент, препятствующий повороту конца
балки. Обычно реакцию
заменяют двумя составляющими –
вертикальной
и горизонтальной
.
Таким образом, можно отметить, что
жёсткая заделка даёт три неизвестные
реакции: вертикальную и горизонтальную
составляющие и реактивный момент.
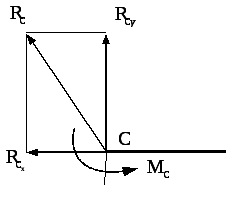
Рис. 7.4
В технике балку с одним защемлённым концом называют консольной балкой, или консолью.
В случае, когда все внешние силы, действующие на балку, направлены перпендикулярно её оси, число неизвестных реакций уменьшается, так как в шарнирно-неподвижной опоре и в жёсткой заделке составляющая реакции, направленная вдоль оси балки, будет равна нулю.