6.4. Определение деформаций при кручении стержня круглого

сечения

Для определения деформаций вала при кручении воспользуемся формулой (6.14):

(6.25)

Взаимный угол поворота сечений на длине равен

, (6.26)

где – жёсткость вала при кручении. Если крутящий момент и жёсткость не изменяются на всём участке интегрирования, то полную деформацию участка вала длинойможно определить по формуле

(6.27)

Эта формула по структуре аналогична формуле для определения деформации при растяжении и сжатии.

Угол закручивания, приходящийся на единицу длины вала, называется относительным углом закручивания:

(6.28)

На практике, кроме требований прочности, часто вводится условие жёсткости, которое заключается в том, что относительный угол закручивания не должен превышать определённую величину, т.е.

(6.29)

Формула (6.29) выражает условие жёсткости. В ней относительный и допускаемый угол закручивания на длине 1 м имеют размерность – радиан. В практикечасто задают в градусах. В этом случае формулу (6.29) можно записать в виде

(6.30)

Отметим, что для валов средних диаметров рекомендуют выбирать равным 0,5⁰ на один метр длины. Из (6.30) можно определить диаметр вала по заданной жёсткости, учитывая, что полярный момент инерции

;

(6.31)

Для полого вала формула расчёта диаметра из условия жёсткости

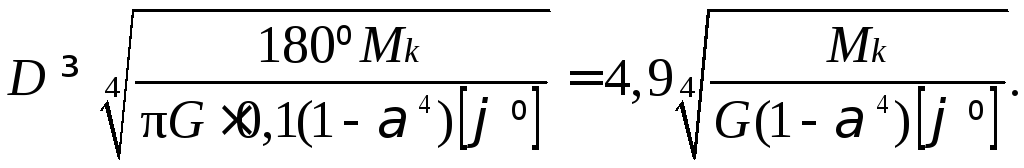(6.32)

Используя формулу (6.27), можно построить эпюру угловых перемещений поперечных сечений вала, нагруженного крутящими моментами. Если рассматривается вращающийся вал, у которого нет неподвижных сечений, то для построения эпюры углов закручивания одно из сечений необходимо принять за условно неподвижное. Примем следующее правило знаков для углов поворота сечений: углы будут считаться положительными, когда сечение, расположенное справа, поворачивается относительно сечения, расположенного слева, по часовой стрелке. При таком условии знак угла закручивания будет совпадать со знаком крутящего момента на участке вала.

Построение эпюры углов закручивания рассмотрим на примере вращающегося вала, нагруженного четырьмя внешними моментами. Построим эпюру крутящих моментов и примем сечение за условно неподвижное (рис. 6.13).

Угол поворота на участке равен нулю, так как на этом участке отсутствует крутящий момент. Сечениеотносительноповернётся на угол, который определим по формуле (6.27). С учётом принятого правила знаков

где М _{К ВС} – крутящий момент на участке ;– длина участка.

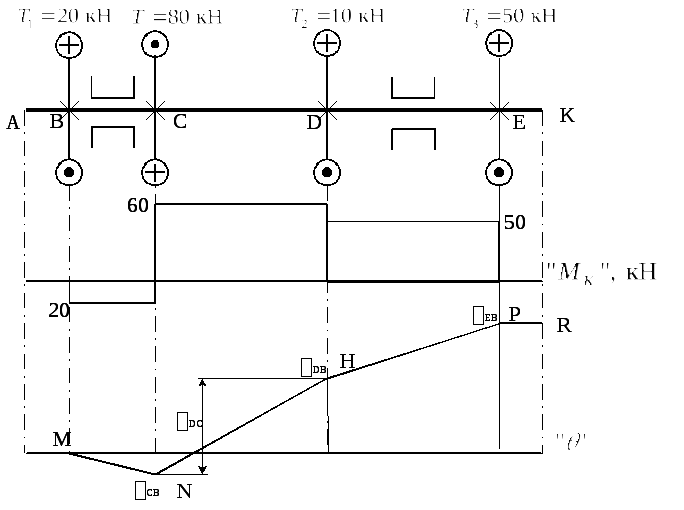
Рис. 6.13

В принятом масштабе [град/мм] отложим ординату . Полученную точкусоединим прямой линией с точкой, так как зависимость угла поворота от длины участка вала линейная. Вычислим угол закручивания сеченияотносительно сечения:

Угол поворота сечения относительно сечения, принятого за неподвижное, определяем как алгебраическую сумму угловотносительноиотносительно:

Аналогично определяем угол закручивания сечения E относительно и затемотносительно:

и .

На участке поворота сечений не происходит, так как крутящий момент на этом участке равен нулю. Все сечения данного участка поворачиваются относительно сеченияна такой же угол, на какой повернулось относительносечение. Участок эпюры здесь будет в виде прямой линии, параллельной оси вала.

7. ПЛОСКИЙ ПОПЕРЕЧНЫЙ ИЗГИБ ПРЯМОГО БРУСА