
- •Сопротивление материалов
- •2.1. Построение эпюр продольных сил
- •2.2. Определение нормальных напряжений в поперечных сечениях
- •2.3. Определение деформаций
- •2.4. Статически неопределимые задачи при осевом растяжении или
- •3.1. Диаграмма растяжения
- •3.2. Твёрдость
- •3.3. Определение допускаемых напряжений и коэффициента запаса
- •4.1. Напряжения в наклонных площадках при осевом растяжении
- •4.2. Напряжения на взаимно-перпендикулярных площадках
- •4.3. Определение напряжений в наклонных сечениях при
- •4.4. Определение главных напряжений и главных площадок
- •4.5. Обобщённый закон Гука
- •5.1. Статические моменты плоских фигур
- •5.2. Моменты инерции плоских сечений
- •5.3. Моменты инерции простых плоских сечений
- •5.4. Центробежный момент инерции
- •5.5. Изменение моментов инерции при повороте осей
- •5.6. Главные оси инерции и главные моменты инерции
- •5.7. Зависимость между моментами инерции относительно
- •5.8. Зависимость между центробежными моментами инерции
- •6.1. Определение напряжений и деформаций при сдвиге
- •6.2. Определение внутренних силовых факторов при кручении
- •6.3. Определение касательных напряжений при кручении
- •6.4. Определение деформаций при кручении стержня круглого
- •7.1. Общие понятия о деформации изгиба
- •7.2. Опоры и опорные реакции балок
- •7.3. Определение опорных реакций
- •7.4. Поперечная сила и изгибающий момент в сечении
- •7.5. Зависимость между изгибающим моментом, поперечной силой
- •7.6. Построение эпюр поперечных сил и изгибающих моментов
- •7.7. Определение нормальных напряжений при изгибе
- •7.8. Условие прочности по нормальным напряжениям
- •7.9. Касательные напряжения при изгибе балки прямоугольного
- •7.10. Аналитический способ определения деформаций при изгибе
- •7.11. Пример определения деформаций при изгибе
- •9.1. Совместное действие изгиба с кручением
- •9.2. Косой изгиб
- •9.3. Сочетание изгиба с растяжением или сжатием
- •9.4. Внецентренное растяжение или сжатие
- •10.1. Устойчивые и неустойчивые формы равновесия
- •10.2. Формула Эйлера для критической силы
- •10.3. Влияние способа закрепления концов стержней
- •10.4. Пределы применимости формулы Эйлера
- •10.5. Практические формулы расчёта на устойчивость
- •Оглавление
- •Троицкий Игорь Витальевич
6.3. Определение касательных напряжений при кручении
стержня круглого сечения
Крутящие моменты представляют собой равнодействующие внутренних сил. При кручении стержня в его поперечных сечениях возникают непрерывно распределённые касательные напряжения, которые нужно уметь определять при расчётах на прочность.
Нанесём на круглый стержень ортогональную сетку и нагрузим его внешним моментом Т (рис. 6.9). По результатам этого опыта можно сделать следующие выводы:

Рис. 6.9
1) прямоугольники ортогональной сетки превратились в параллелограммы, следовательно, в поперечных сечениях действуют касательные напряжения;
2) расстояния
между линиями, нормальными оси стержня,
и длина всего стержня не изменились. Не
изменился также и диаметр стержня. Можно
предположить, что каждое поперечное
сечение поворачивается в своей плоскости
на некоторый угол, оставаясь плоским и
нормальным к оси (гипотеза Бернулли).
На основании этой гипотезы делаем вывод
о том, что радиусы всех поперечных
сечений повернулись на определённые
углы, оставаясь прямолинейными. Таким
образом, точка
К переместится
в положение К´
по дуге радиуса r,
а точка N
– в
![]() по дуге меньшего радиуса
по дуге меньшего радиуса![]() (рис. 6.10).
(рис. 6.10).
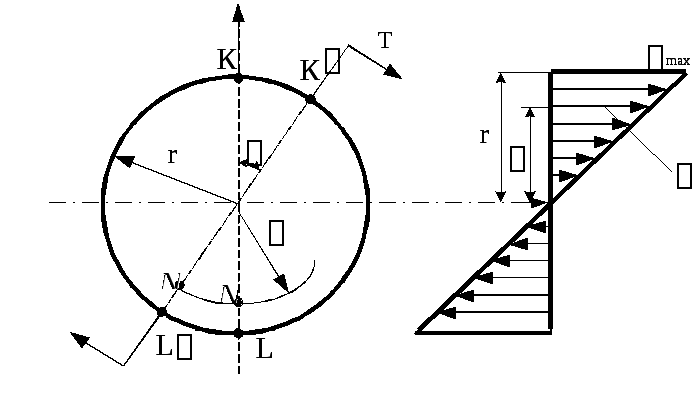
Рис. 6.10
На основании этого можно сделать вывод, что при кручении круглого стержня в его поперечных сечениях действуют только касательные напряжения, а нормальные напряжения отсутствуют, т.е. мы имеем случай чистого сдвига.
Для того чтобы установить закон распределения касательных напряжений по поперечному сечению круглого стержня, нагруженного крутящим моментом Т, рассмотрим его деформацию между сечениями I и II (рис. 6.9 и рис. 6.11).
Угол сдвига элемента ABCD, расположенного на поверхности стержня:
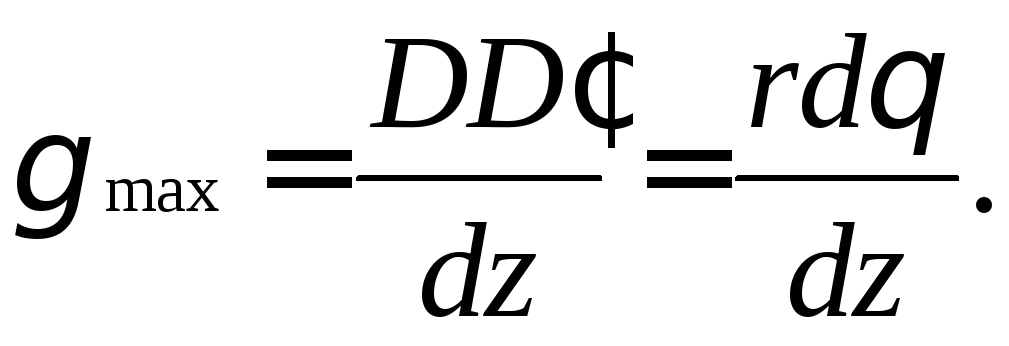
Угол сдвига
элемента, расположенного на расстоянии
![]() от оси стержня:
от оси стержня:
![]() (6.10)
(6.10)

Рис. 6.11
На основании закона Гука для сдвига можно записать
![]() (6.11)
(6.11)
Из (6.11) следует,
что при кручении касательные напряжения
![]() и деформации
и деформации![]() прямо пропорциональны расстоянию от
центра тяжести сечения. В центре тяжести
круглого сечения касательные напряжения
равны нулю, наибольшее значение они
принимают на поверхности стержня. Эпюра
касательных напряжений в поперечном
сечении круглого стержня изображена
на рис. 6.10.
прямо пропорциональны расстоянию от
центра тяжести сечения. В центре тяжести
круглого сечения касательные напряжения
равны нулю, наибольшее значение они
принимают на поверхности стержня. Эпюра
касательных напряжений в поперечном
сечении круглого стержня изображена
на рис. 6.10.
Определим касательные напряжения из условия, что крутящий момент в сечении представляет собой равнодействующий момент от касательных напряжений (рис. 6.12).
![]() ,
(6.12)
,
(6.12)
где
![]() – элементарная сила, действующая на
площадке
– элементарная сила, действующая на
площадке![]() .
.
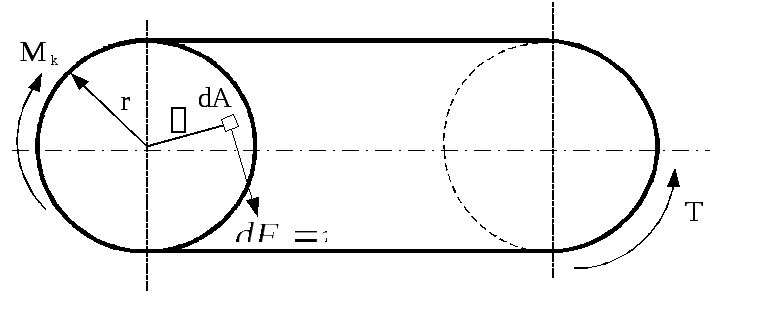
Рис. 6.12
Подставим в (6.12) касательные напряжения из (6.11):
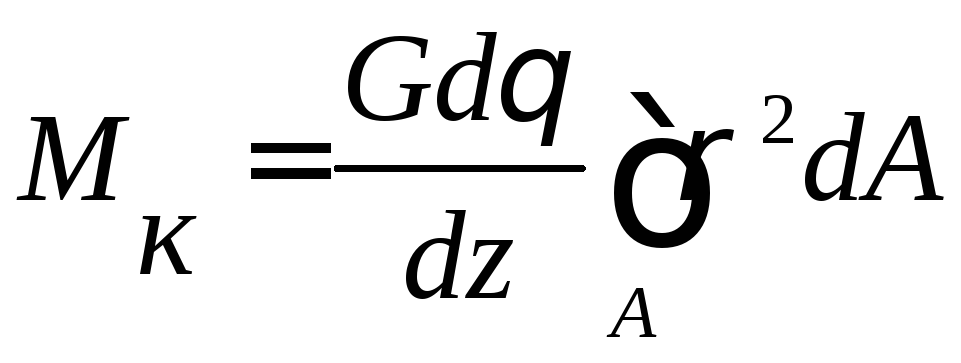 .
(6.13)
.
(6.13)
Интеграл
![]() представляет собой полярный момент
инерции круглого сеченияJp
,
следовательно,
представляет собой полярный момент
инерции круглого сеченияJp
,
следовательно,
![]() ,
откуда
,
откуда
![]() (6.14)
(6.14)
Подставим значение
![]() в формулу (6.11) и получим
в формулу (6.11) и получим
![]() (6.15)
(6.15)
Из (6.15) следует,
что в точках, равноудалённых от центра
сечения, касательные напряжения
одинаковы. Наибольшие напряжения
![]() возникают в точках, расположенных на
поверхности стержня, где
возникают в точках, расположенных на
поверхности стержня, где![]() .
.
![]() (6.16)
(6.16)
где величина
![]() ,
представляющая геометрическую
характеристику плоского сечения, носит
название полярного момента сопротивления
или момента сопротивления при кручении:
,
представляющая геометрическую
характеристику плоского сечения, носит
название полярного момента сопротивления
или момента сопротивления при кручении:
![]() (6.17)
(6.17)
Для круглого сплошного сечения
![]() .
(6.18)
.
(6.18)
Для кольцевого сечения (рис. 5.5)
![]() (6.19)
(6.19)
где
![]() .
.
Запишем условие
статической прочности при кручении,
обозначив допускаемое касательное
напряжение через
![]()
![]() (6.20)
(6.20)
Величину
![]() принимают равной 0,5 – 0,6 допускаемого
напряжения на растяжение. Уравнение
(6.20) можно использовать только для
круглых валов, как сплошных, так и полых;
для валов других сечений его применять
нельзя. Используя условие прочности,
можно рассчитать диаметр вала либо
определить максимальный допускаемый
крутящий момент, который может передать
вал. Подставим в формулу (6.20) выражение
полярного момента сопротивления
принимают равной 0,5 – 0,6 допускаемого
напряжения на растяжение. Уравнение
(6.20) можно использовать только для
круглых валов, как сплошных, так и полых;
для валов других сечений его применять
нельзя. Используя условие прочности,
можно рассчитать диаметр вала либо
определить максимальный допускаемый
крутящий момент, который может передать
вал. Подставим в формулу (6.20) выражение
полярного момента сопротивления
![]() (6.21)
(6.21)
откуда
 (6.22)
(6.22)
Аналогично для полых валов можно записать
 (6.23)
(6.23)
Допускаемый из условия статической прочности при кручении
максимальный крутящий момент определяют по формуле
![]() (6.24)
(6.24)
