
- •9. Виды отношений
- •Примеры рефлексивных отношений
- •Примеры антирефлексивных отношений
- •Свойства
- •Примеры
- •Примеры отношений эквивалентности
- •14. Конъюнкция
- •Дизъюнкция
- •Отрицание
- •16. Метод математической индукции
- •17. Элементы комбинаторики.
- •22. Формула де-Моргана:
- •Ориентированный граф
- •Смешанный граф
- •Изоморфные графы
- •Эйлеровы графы
16. Метод математической индукции
Метод математической индукции является важным способом доказательства предложений (утверждений), зависящих от натурального аргумента.
Метод математической индукции состоит в следующем:
Предложение (утверждение) P(n), зависящее от натурального числа n, справедливо для любого натурального n если:
1.P(1) является истинным предложением (утверждением);
2.P(n) остается истинным предложением (утверждением), если n увеличить на единицу, то есть P(n + 1) - истинное предложение (утверждение).
Таким образом метод математической индукции предполагает два этапа:
1.Этап проверки: проверяется, истинно ли предложение (утверждение) P(1).
2.Этап доказательства: предполагается, что предложение P(n) истинно, и доказывается истинность предложения P(n + 1) (n увеличено на единицу).
Пример: Доказать следующие равенства
![]()
При n =
1 равенство примет вид ![]() 1=1
, следовательно, P(1)
истинно
1=1
, следовательно, P(1)
истинно
При
P(n +1),

истинно. Поскольку
![]()
получим
![]()
то есть, P(n + 1) - истинное утверждение.
Таким образом, согласно методу математической индукции, исходное равенство справедливо для любого натурального n.
17. Элементы комбинаторики.
Если из множества, содержащего m элементов, требуется выбрать какие-то k элементов, то возникает вопрос: сколькими способами это можно сделать и какие подмножества при этом получаются. Такие задачи называются комбинаторными, а соответствующий раздел математики – комбинаторикой.
Все формулы для подсчета числа решений в комбинаторных задачах опираются на правило произведения: если элемент X можно выбрать k способами, а элемент Y можно выбрать n способами, то пару XY можно составить kn способами.
Размещение
с повторением. Из
множества, содержащего m элементов,
нужно выбрать k элементов,
причем выбранный элемент, после того,
как его взяли, вновь возвращается в
исходное множество (то есть элементы в
выбранном множестве могут повторяться).
Пользуясь правилом произведения,
получим, что каждый из k элементов
может быть выбран m способами.
Таким образом, общее число комбинаций
равно ![]() .
.
Пример. Сколько различных четырехзначных чисел можно составить из цифр 2, 3, 5, 7.
Решение. Первой
цифрой в числе может быть любая из
четырех имеющихся. То же самое можно
сказать и о последующих цифрах числа,
поэтому общее число комбинаций: ![]()
Размещение
без повторений.
Из множества, содержащего m различных
элементов, надо выбрать упорядоченное
подмножество из k элементов
(k
m),
то есть такое подмножество, в котором
элементы располагаются в определенном
порядке, и изменение порядка элементов
изменяет подмножество. Кроме этого,
элементы в выбранном подмножестве не
повторяются. Требуется выяснить, сколько
таких комбинаций существует. По правилу
произведения получаем, что первый
элемент можно выбрать m способами,
второй элемент – (m-1)
способом, и так далее, а элемент с
номером k можно
выбрать (m – k +
1) способами. Следовательно, число
упорядоченных k-элементных
подмножеств, взятых из множества,
содержащего m элементов
равно m(m-1)(m-2)…(m-k+1).
Такие подмножества называются размещениями
из m элементов
по k элементов,
а их общее число можно выразить формулой 
Пример. Сколько различных четырехзначных чисел можно составить из цифр 1, 2, 3, 4, 5, 6, при условии. Что цифры в числе не повторяются?
Решение. Общее
число комбинаций равно числу размещений
из 6 элементов по 4: 
Перестановки. Пусть
множество содержит m различных
элементов. Рассмотрим все возможные
варианты перестановок элементов этого
множества. Получаемые при этом
упорядоченные множества отличаются
друг от друга только порядком входящих
в них элементов. Такие упорядоченные
множества называются перестановками.
Число перестановок из m элементов
равно: ![]()
Пример. Сколько различных четырехзначных чисел можно составить из цифр 2, 3, 5. 7, если цифры в числе не повторяются?
Решение. Количество
чисел равно числу перестановок из
четырех элементов: ![]()
Сочетания. Пусть
из множества, содержащего m различных
элементов, требуется выбрать подмножество,
содержащее k различных
элементов (k m).
Получаемые при этом подмножества не
упорядочены. Такие неупорядоченные
подмножества называются сочетаниями.
Число сочетаний из m элементов
по k
элементов вычисляется по формуле: 
Пример. В группе 10 студентов. Сколькими способами можно выбрать из этой группы троих студентов для участия в конференции?
Решение. Число
способов равно числу сочетаний из 10
элементов по 3 элемента:  .
.
18.
Полином Жегалкина —
многочлен над кольцом ![]() ,
то есть полином с
коэффициентами вида 0 и 1, где в качестве
произведения берётся конъюнкция,
а в качестве сложения —исключающее
или.
Полином был предложен
в 1927 году Иваном Жегалкиным в
качестве удобного средства для
представления функций
булевой логики.
В зарубежной литературе представление
в виде полинома Жегалкина обычно
называется алгебраической нормальной
формой (АНФ).
,
то есть полином с
коэффициентами вида 0 и 1, где в качестве
произведения берётся конъюнкция,
а в качестве сложения —исключающее
или.
Полином был предложен
в 1927 году Иваном Жегалкиным в
качестве удобного средства для
представления функций
булевой логики.
В зарубежной литературе представление
в виде полинома Жегалкина обычно
называется алгебраической нормальной
формой (АНФ).
Теорема Жегалкина — утверждение о существовании и единственности представления всякой булевой функции в виде полинома Жегалкина.
Полином Жегалкина представляет собой сумму по модулю два произведений неинвертированных переменных, а также (если необходимо) константы 1. Формально полином Жегалкина можно представить в виде
![]()
![]()
или в более формализованном виде как:

Примеры полиномов Жегалкина:
![]()
![]()
![]()
19.
Конъюнкцией
предикатов
 называют предикат
называют предикат определенный на том же множестве и
обращающийся в истинное высказывание
при тех и только тех
определенный на том же множестве и
обращающийся в истинное высказывание
при тех и только тех ,
при которых оба предиката обращаются
в истинные высказывания:
,
при которых оба предиката обращаются
в истинные высказывания:

Дизъюнкцией
предикатов
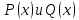 называют предикат
называют предикат определенный на том же множестве и
обращающийся в истинное высказывание
при тех и только тех
определенный на том же множестве и
обращающийся в истинное высказывание
при тех и только тех ,
при которых хотя бы один из этих предикатов
обращается в истинное высказывание:
,
при которых хотя бы один из этих предикатов
обращается в истинное высказывание:
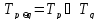
Отрицанием
предиката
 называют предикат
называют предикат определенный на том же множестве и
обращающийся в истинное высказывание
при тех значения
определенный на том же множестве и
обращающийся в истинное высказывание
при тех значения ,
при которых
,
при которых обращается в ложное высказывание, т.е.
обращается в ложное высказывание, т.е.

20.Импликацией
предикатов
 называют предикат
называют предикат определенный на том же множестве и
обращающийся в да ложное высказыванием
при тех и только тех
определенный на том же множестве и
обращающийся в да ложное высказыванием
при тех и только тех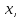 при которых
при которых обращаются в истинные высказывания, а
обращаются в истинные высказывания, а ложное. Согласно данному определению
область ложности импликации предикатов
находят по формуле
ложное. Согласно данному определению
область ложности импликации предикатов
находят по формуле

А область истинности импликации предикатов по формуле

Эквиваленцией
предикатов
 называют предикат
называют предикат
Определенный
на том же множестве и обращающийся в
истинное высказывание при тех и только
тех
 при которых
при которых обращаются оба в истинные высказывания
или оба в ложные.
обращаются оба в истинные высказывания
или оба в ложные.
Пользуясь данным определением, можно записать формулу для нахождения области истинности эквиваленции предикатов:

Последнюю формулу можно записать иначе:

21.
Формула
бинома Ньютона для
натуральных n имеет
вид  ,
где
,
где  - биномиальные
коэффициенты,
представляющие из себя сочетания
из n по k, k=0,1,2,…,n,
а "!" – это знак факториала).
- биномиальные
коэффициенты,
представляющие из себя сочетания
из n по k, k=0,1,2,…,n,
а "!" – это знак факториала).
К
примеру, известная формула сокращенного
умножения "квадрат суммы" вида ![]() есть
частный случай бинома Ньютона при n=2.
есть
частный случай бинома Ньютона при n=2.
Выражение,
которое находится в правой части формулы
бинома Ньютона, называютразложением выражения (a+b)n,
а выражение ![]() называют (k+1)-ым
членом разложения, k=0,1,2,…,n.
называют (k+1)-ым
членом разложения, k=0,1,2,…,n.
