
- •Федеральное агенство морского и речного
- •2. Начальные условия и задача коши
- •3. Общее решение и общий интеграл
- •4. Метод разделения переменных
- •5. Однородное уравнение первого порядка
- •6. Линейное уравнение первого порядка
- •7. Уравнения, допускающие понижение порядка
- •7.1. Уравнение вида
- •7.2. Уравнение, не содержащее явно неизвестную функцию y
- •7.3. Уравнение, не содержащее явно независимую переменную X
- •8. Линейное уравнение второго порядка
- •8.1. Основные понятия
- •8.2. Свойства решений однородного линейного уравнения
- •8.3. Линейное уравнение с постоянными коэффициентами
- •8.4. Структура общего решения неоднородного линейного уравнения.
- •9. Метод вариации произвольных постоянных
- •10. Метод неопределенных коэффициентов
- •Литература
- •Часть 1,2. М.: "Оникс 21 век". – 2003.
- •Михаил Юрьевич Ястребов
- •Дифференциальные уравнения
- •Учебное пособие
4. Метод разделения переменных
Определение. Уравнением с разделенными переменными называется дифференциальное уравнение первого порядка вида
![]() ,
(4)
,
(4)
с
непрерывными функциями
![]() и
и![]()
Смысл
этого термина заключается в том, что
переменные
![]() и
и![]() разделены по разным частям равенства
(4).
разделены по разным частям равенства
(4).
Напомним,
что, согласно определению, дифференциал
функции
![]() есть произведение производной на
дифференциал независимой переменной:
есть произведение производной на
дифференциал независимой переменной:![]() .
Если умножить обе части равенства (4) на
.
Если умножить обе части равенства (4) на![]() ,
получим:
,
получим:
![]() .
(5)
.
(5)
Это другой, более традиционный способ записи уравнения с разделенными переменными.
Теорема.
Если в уравнении (5) функции
![]() и
и![]() имеют первообразные
имеют первообразные![]() и
и![]() ,
то общий интеграл уравнения имеет вид:
,
то общий интеграл уравнения имеет вид:
![]() ,
(6)
,
(6)
где
![]() —
произвольная постоянная.
—
произвольная постоянная.
Замечание. Если для обозначения первообразных использовать символ неопределенного интеграла, то общий интеграл записывается в виде:
![]() .
(7)
.
(7)
Доказательство.
Опуская доказательство того, что
уравнение (6) действительно задает
неявную функцию
![]() ,
убедимся, что
,
убедимся, что![]() удовлетворяет уравнению (4). Для этого
продифференцируем по
удовлетворяет уравнению (4). Для этого
продифференцируем по![]() равенство (6), применяя для левой части
правило производной сложной функции с
промежуточной переменной
равенство (6), применяя для левой части
правило производной сложной функции с
промежуточной переменной![]() :
:
![]() ,
,
или,
учитывая, что
![]() и
и![]() первообразные для
первообразные для![]() и
и![]() :
:
![]() .
.
Остается
убедиться, что за счет выбора значения
произвольной постоянной
![]() можно обеспечить выполнение любых
начальных условий
можно обеспечить выполнение любых
начальных условий![]() .
Подставляя начальные условия в (6),
получаем:
.
Подставляя начальные условия в (6),
получаем:
![]() .
▄
.
▄
Примеры.
1. Для уравнения
![]() найдем общий интеграл и частный интеграл
для начальных условий
найдем общий интеграл и частный интеграл
для начальных условий .
Имеем:
.
Имеем:
![]()
![]() —
—
это общий интеграл.
Подставим
теперь в общий интеграл начальные
условия и найдем соответствующее
значение константы
![]() :
:
 .
.
Следовательно, частный интеграл, дающий решение задачи Коши, имеет вид:
![]() .
.
2.
Рассмотрим уравнение
 с начальными условиями
с начальными условиями![]() .
Умножая обе части уравнения на
.
Умножая обе части уравнения на![]() и затем интегрируя, получаем:
и затем интегрируя, получаем:
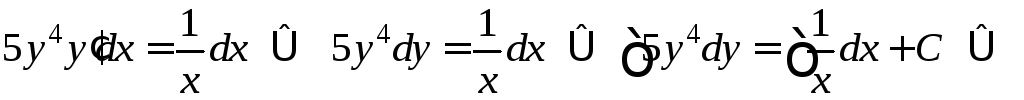
![]() –это
общий интеграл. Выражая отсюда явно
–это
общий интеграл. Выражая отсюда явно
![]() через
через![]() и
и![]() ,
получаем общее решение:
,
получаем общее решение: .
Подстановка начальных условий в общее
решение дает:
.
Подстановка начальных условий в общее
решение дает: ,
так что
,
так что![]() .
Следовательно, функция
.
Следовательно, функция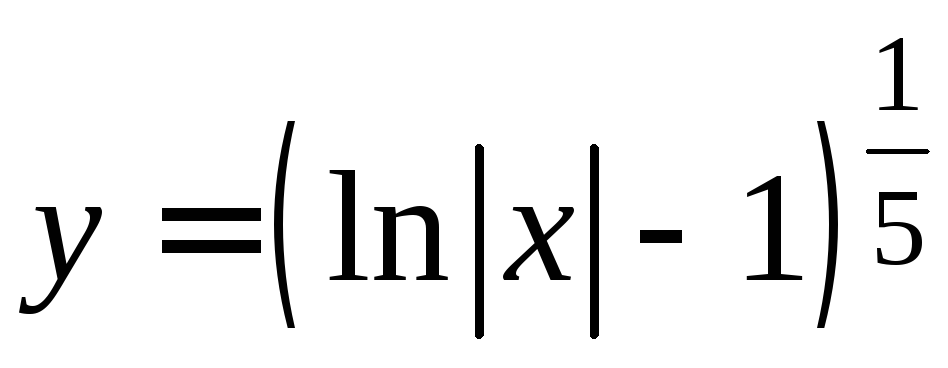 является решением задачи Коши.
является решением задачи Коши.
Определение. Уравнением с разделяющимися переменными называется дифференциальное уравнение первого порядка вида
![]() ,
(8)
,
(8)
с
непрерывными функциями
![]() .
.
В
этом уравнении каждая из частей является
произведением двух множителей, один из
которых зависит только от
![]() ,
а другой – только от
,
а другой – только от![]() .
.
От
этого уравнения легко перейти к уравнению
с разделенными переменными, деля обе
части на произведение
![]() («разделяя переменные»):
(«разделяя переменные»):
 .
.
Примеры.
1.
 .
Обе части разделим на
.
Обе части разделим на![]() и умножим на
и умножим на![]() :
: .
Интегрируем:
.
Интегрируем:

 —
—
общий интеграл.
2.
![]() ;
начальные условия:
;
начальные условия: .
Записываем производную
.
Записываем производную![]() как отношение дифференциалов:
как отношение дифференциалов:
 .
.
Обе
части умножим на
![]() ,
разделим на
,
разделим на![]() и проинтегрируем:
и проинтегрируем:
 —
—
общий интеграл. Найдем теперь частный интеграл, удовлетворяющий начальным условиям. Подставляя начальные условия в полученное уравнение, имеем:
 ;
;
 .
.
Следовательно, частный интеграл, дающий решение задачи Коши, имеет вид:
 .
.
5. Однородное уравнение первого порядка
Определение. Однородным уравнением первого порядка называется уравнение, разрешенное относительно производной:
![]() ,
(9)
,
(9)
в
котором функция
![]() при всех вещественных
при всех вещественных![]() удовлетворяет условию:
удовлетворяет условию:
![]() .
.
Полагая
в этом равенстве
 ,
убеждаемся, что правая часть зависит
только от отношения переменных
,
убеждаемся, что правая часть зависит
только от отношения переменных![]() :
: .
.
Приведем примеры таких функций:
1)
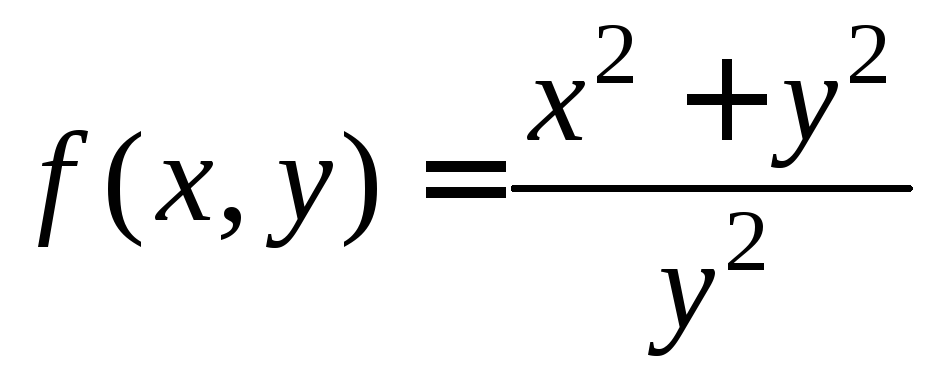 ;
2)
;
2)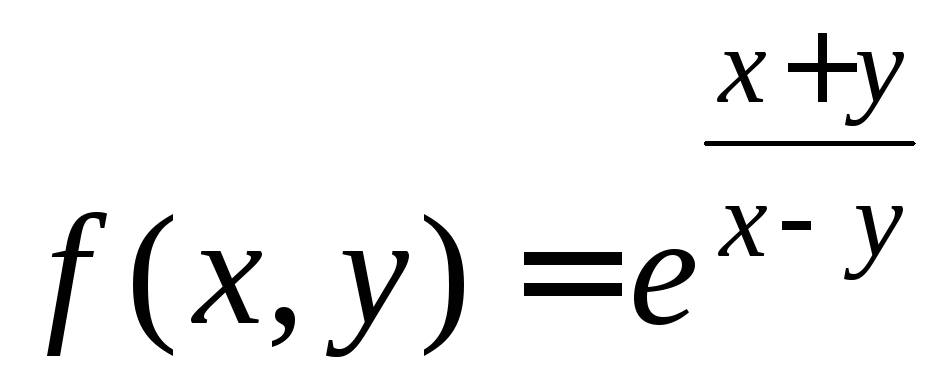 .
Напротив, функция
.
Напротив, функция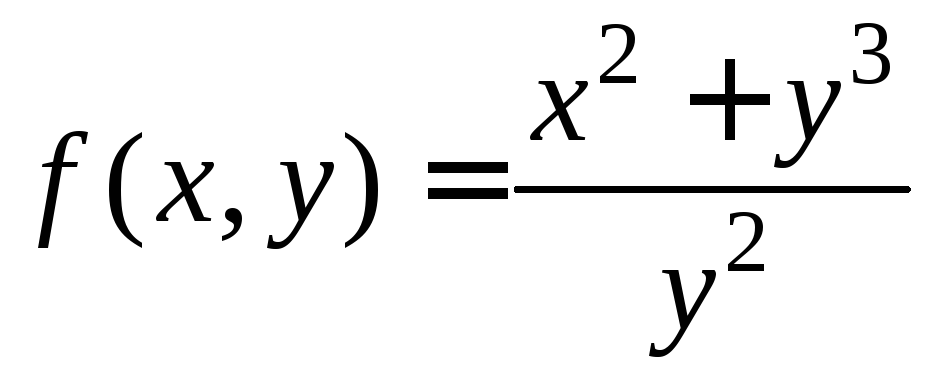 ,
как легко проверить, не удовлетворяет
условию
,
как легко проверить, не удовлетворяет
условию![]() .
.
Введем
новую искомую функцию
 ,
так что
,
так что![]() .
Тогда формула для производной произведения
дает:
.
Тогда формула для производной произведения
дает:![]() ,
и уравнение (9) принимает вид:
,
и уравнение (9) принимает вид:
 —
—
уравнение
с разделяющимися переменными относительно
новой искомой функции
![]() .
Если для него найден общий интеграл
(методом, описанным в предыдущем разделе):
.
Если для него найден общий интеграл
(методом, описанным в предыдущем разделе):
![]() ,
,
то,
заменяя в нем
![]() на
на![]() ,
получим общий интеграл для исходной
неизвестной функции
,
получим общий интеграл для исходной
неизвестной функции![]() :
:
 .
.
Алгоритм решения однородного уравнения первого порядка:
1.
Проверка однородности:
![]() .
.
2.
Введение новой искомой функции
 .
.
3.
Замена в уравнении ![]() на
на![]() ,
,![]() на
на![]() .
.
4.
Решение полученного уравнения с
разделяющимися переменными относительно
![]() .
.
5.
Замена в полученном общем интеграле
![]() на
на![]() .
.
Пример.
Решим уравнение
 .
Здесь
.
Здесь ,
так что уравнение, действительно,
является однородным. После введения
новой переменной
,
так что уравнение, действительно,
является однородным. После введения
новой переменной![]() получаем уравнение:
получаем уравнение:

 .
.
Заменяя
![]() на
на![]() ,
получаем общий интеграл для исходной
неизвестной функции
,
получаем общий интеграл для исходной
неизвестной функции![]() :
: .
.
