
- •§ 1. Понятие функции двух переменных.
- •§ 2. Частные производные и дифференциалы функции двухпеременных.
- •§ 4. Дифференцирование сложных функций.
- •§ 5. Дифференцирование неявной функции.
- •§ 6. Производная по направлению, градиент.
- •§ 7. Касательная плоскость и нормаль к поверхности.
- •§ 8. Локальный экстремум функции нескольких переменных.
- •§ 9. Условный экстремум функции.
- •§ 10. Найти наибольшее и наименьшее значение функции в замкнутой области.
Дифференциальное исчисление функции нескольких переменных.
Совместное изменение двух переменных, из которых одна зависит от другой, при этом значение независимой переменной полностью определяет значение зависимой переменной, является идеальным случаем. В науке и на практике обычно оказывается, что независимых переменных бывает несколько, и для определения значения функции необходимо предварительно установить значения, совместно принимаемые всеми этими независимыми переменными.
Так,
например, изучая физико-химическое
состояние какой-либо системы, часто
приходится наблюдать изменение ее
свойств от точки к точке, таких как
температура, давление, концентрация,
плотность и т.п. Все эти величины зависят
от координат точки
![]() .
Если физико-химическое состояние системы
меняется во времени, то к этим независимым
переменным добавляется еще и время
.
Если физико-химическое состояние системы
меняется во времени, то к этим независимым
переменным добавляется еще и время
![]() .
В этом случае приходится исследовать
функцию от четырех переменных. На
практике количество независимых
переменных обычно ограничивается
целесообразной степенью точности
используемой модели.
.
В этом случае приходится исследовать
функцию от четырех переменных. На
практике количество независимых
переменных обычно ограничивается
целесообразной степенью точности
используемой модели.
§ 1. Понятие функции двух переменных.
Говоря
об изменении двух независимых переменных
![]() и
и![]() ,
следует указывать, какие пары значений
,
следует указывать, какие пары значений
![]() они могут принимать совместно. Множество
они могут принимать совместно. Множество
![]() этих
пар называется областью изменения
переменных
этих
пар называется областью изменения
переменных![]() илиобластью
определения функции.
илиобластью
определения функции.
Переменная
![]() (с областью изменения
(с областью изменения![]() )
называетсяфункцией
независимых переменных
)
называетсяфункцией
независимых переменных
![]() на множестве
на множестве![]() ,
если каждой паре
,
если каждой паре
![]() из области
из области
![]() ставится в соответствие одно определенное
значение
ставится в соответствие одно определенное
значение![]() из множества
из множества![]() .
Обозначается как
.
Обозначается как
![]() .
Пример
1. Найти и изобразить
область определения функции.
.
Пример
1. Найти и изобразить
область определения функции.
![]()
Решение. Данная функция определена, если
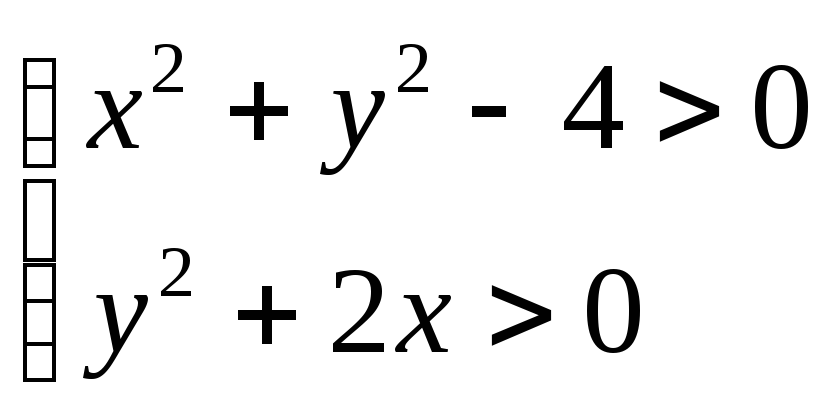
Следовательно, областью определения функции является пересечение множеств на плоскости:
![]()
Изобразим область определения на рисунке
![]()
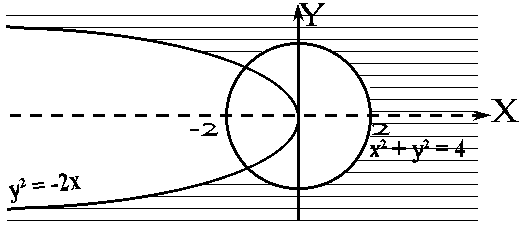
Примеры для самостоятельной работы:
Найти и изобразить на плоскости область определения функции.
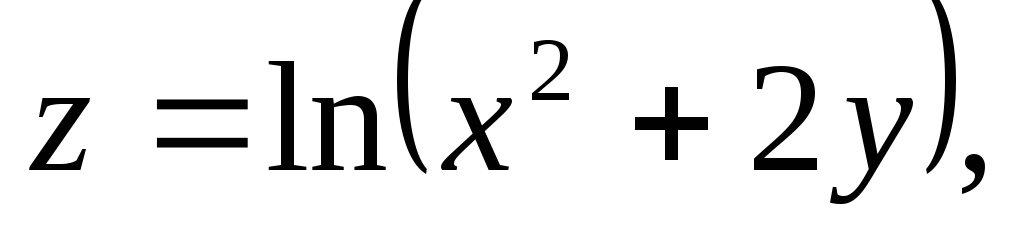
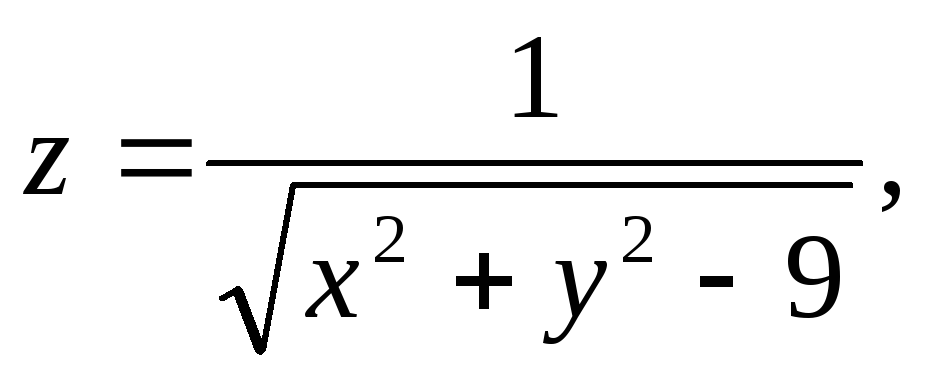
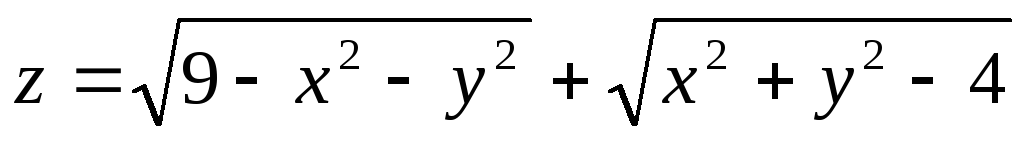 ,
,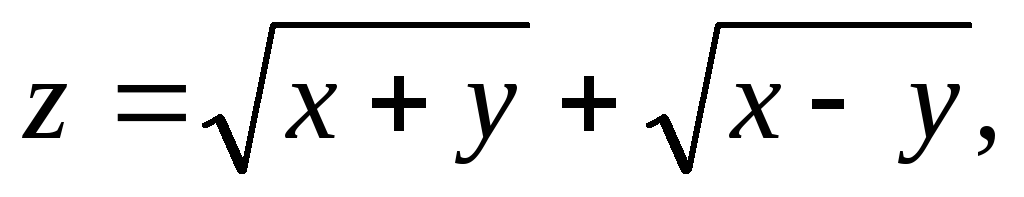

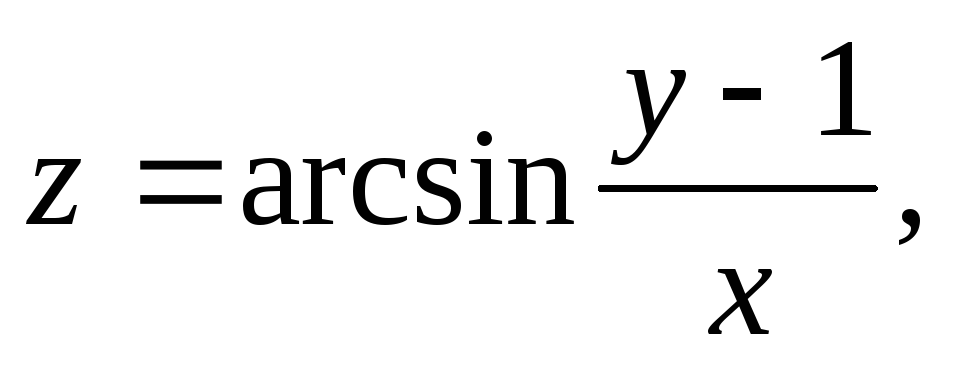
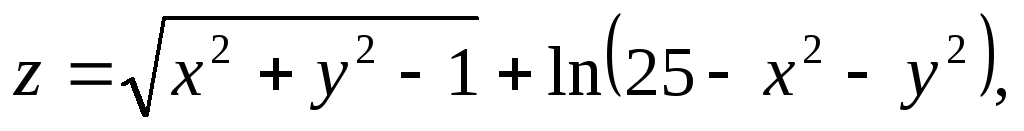
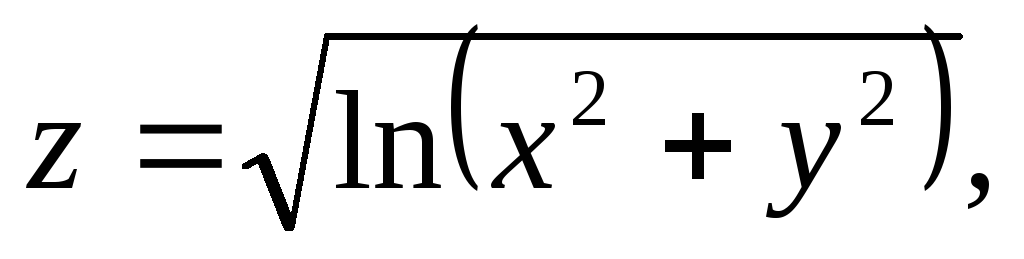
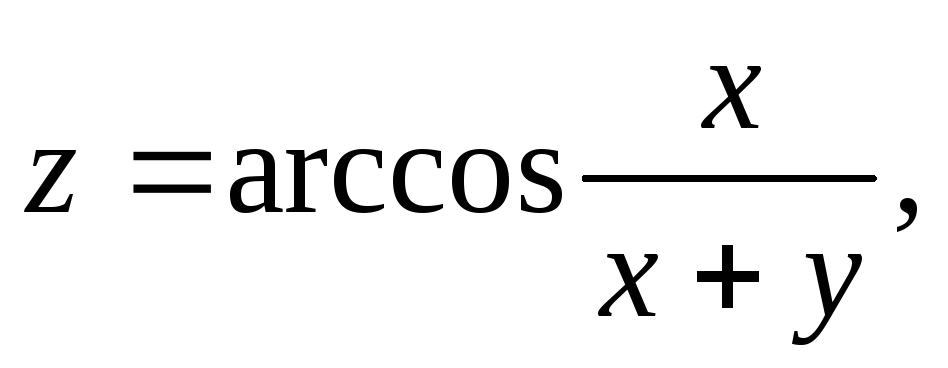
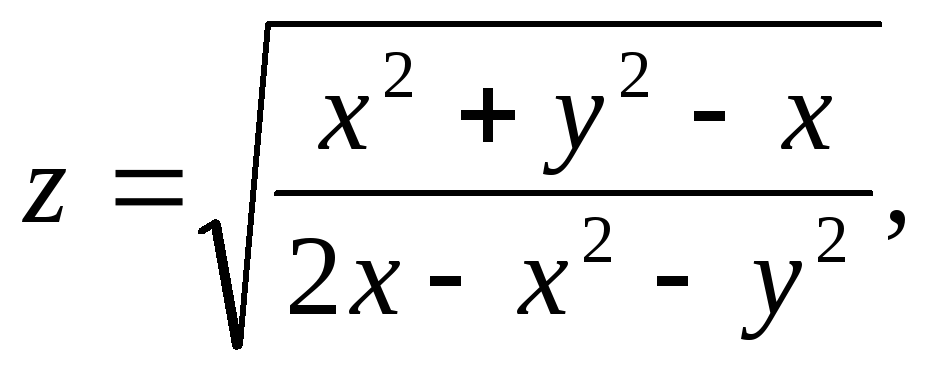
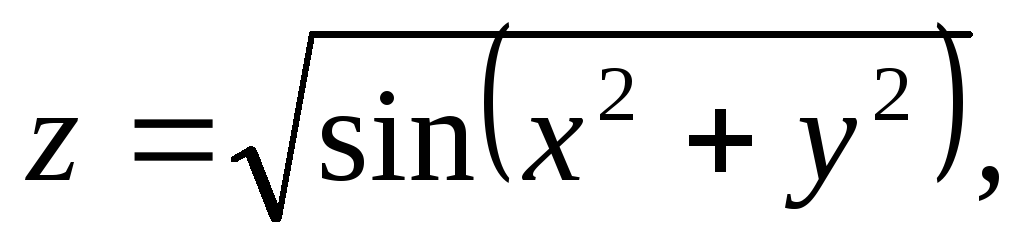
 ,
,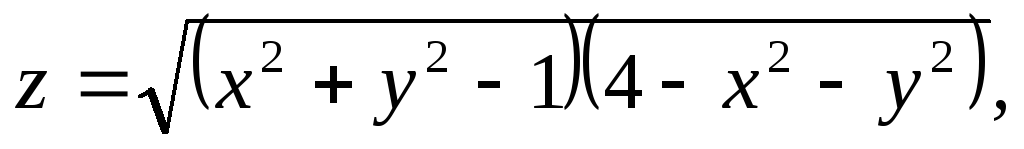
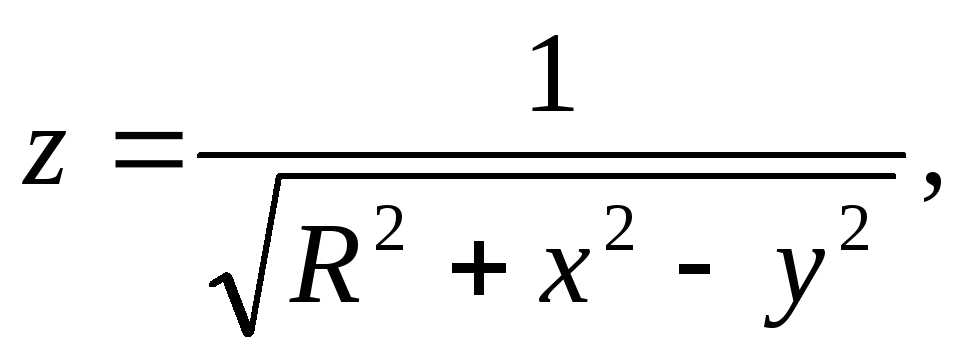
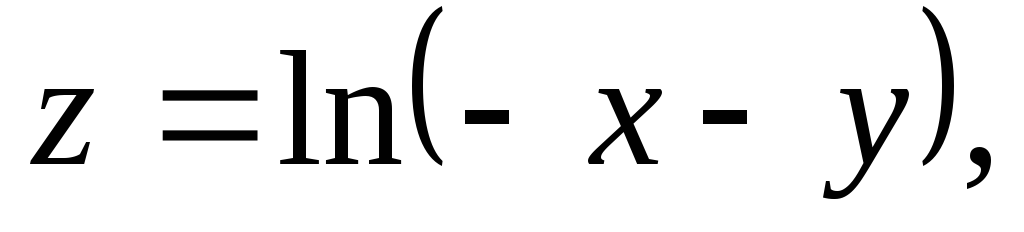
Найти линии уровня функции.
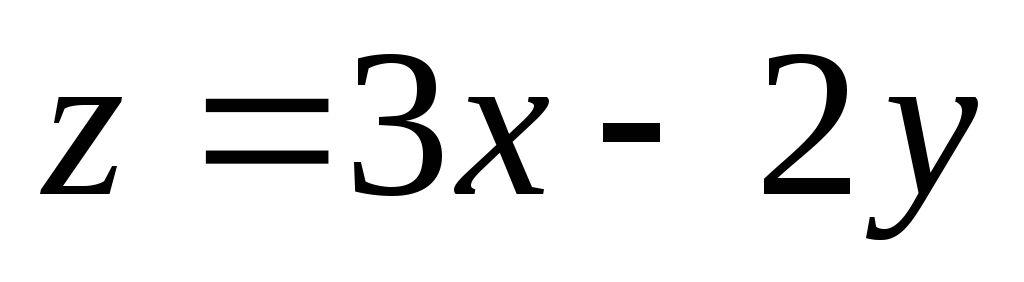 ,
,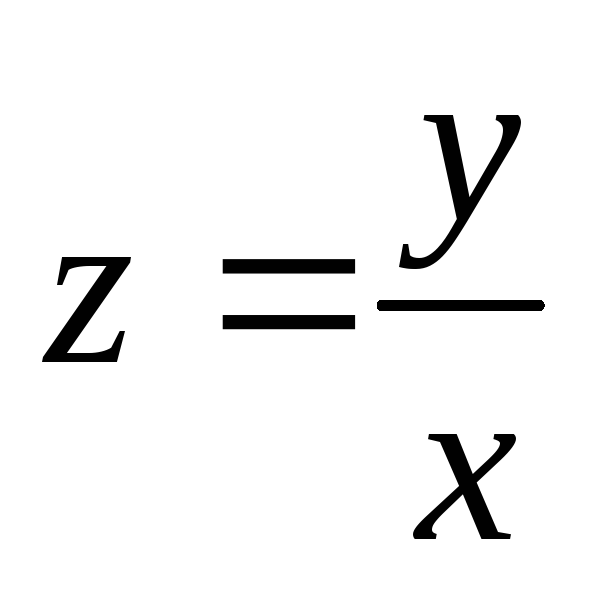 ,
,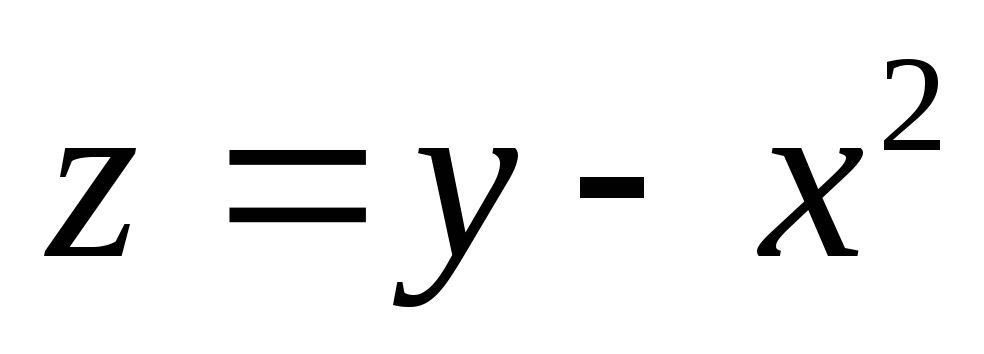 ,
,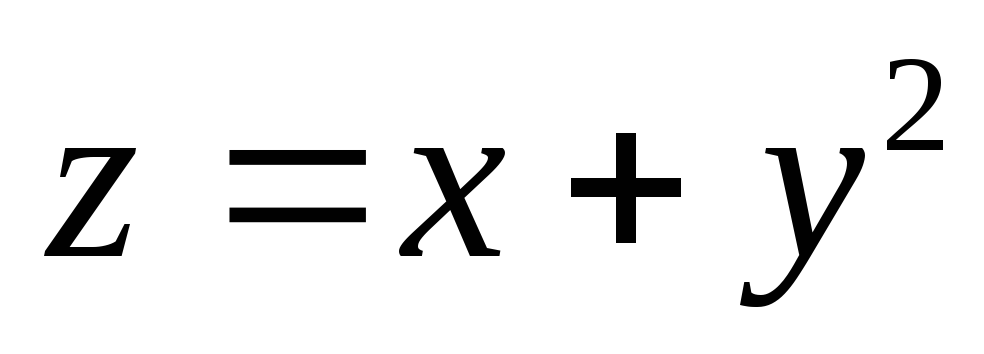 .
.
Вычислить предел функции.
 ,
,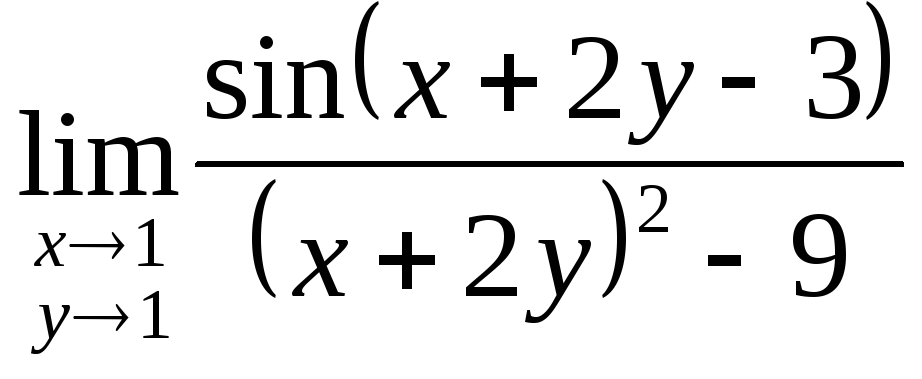 ,
,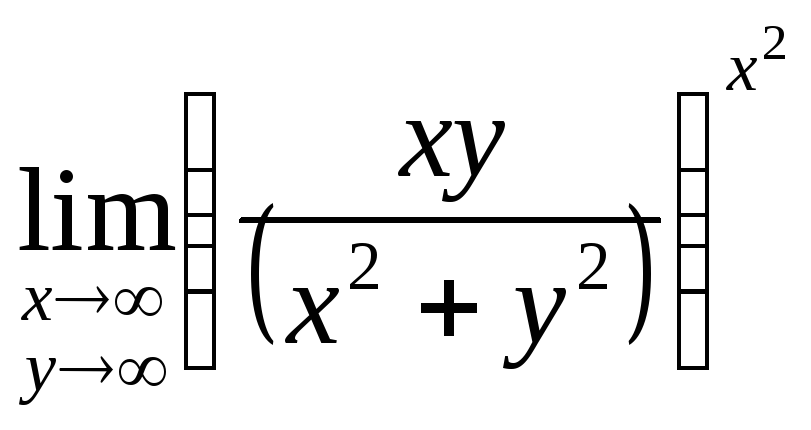 ,
,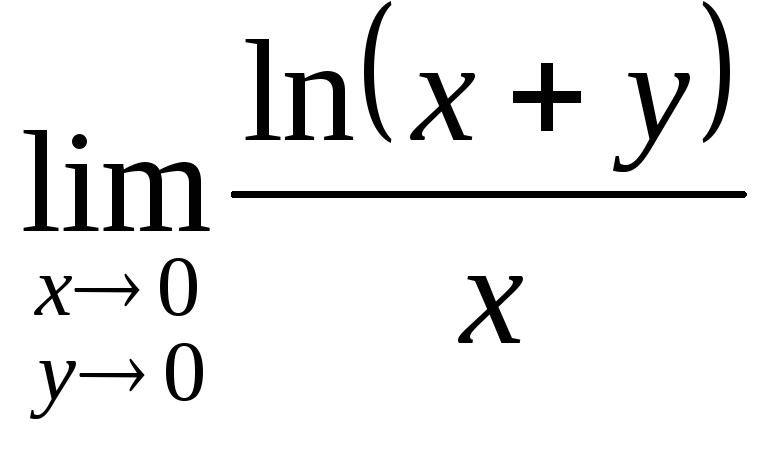 ,
,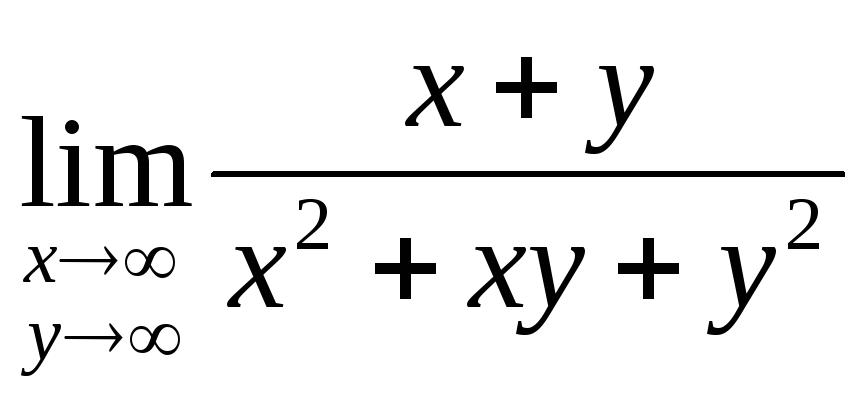 ,
,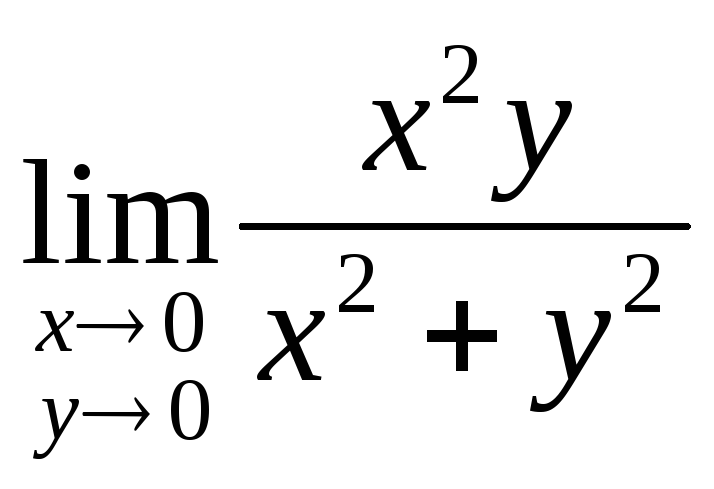 .
.
§ 2. Частные производные и дифференциалы функции двухпеременных.
Частной
производной
по переменной
![]() функции
функции
![]() в точке
в точке![]() называется конечный предел отношения
частного приращения
называется конечный предел отношения
частного приращения![]()
к
приращению
![]() при стремлении
при стремлении![]() к
нулю, если этот предел существует.
к
нулю, если этот предел существует.![]()
![]()
![]()
![]() (1)
(1)
Аналогично
определяется частная производная по
![]()
![]() (2)
(2)
Частные
производные от функции
![]() и
и![]() называютсячастными
производными второго порядка
для функции
называютсячастными
производными второго порядка
для функции
![]() .
Обозначаются:
.
Обозначаются:
![]() ,
,
![]() ,
,![]() ,
,![]() (3)
(3)
Если
![]() и
и![]() определены в некоторой окрестности
точки
определены в некоторой окрестности
точки![]() и непрерывны в точке
и непрерывны в точке![]() ,
тогда
,
тогда
![]() =
=![]() .
(4)
.
(4)
Полным
дифференциалом
![]() функции
функции![]() в точке
в точке![]() ,
называется выражение вида:
,
называется выражение вида:
![]() (5)
(5)
Дифференциалом
второго
порядка
называется полный дифференциал от ее
дифференциала первого порядка,
вычисленный в точке
![]()
![]() (6)
(6)
Пример 2. Дана
функция
![]() .
Найти: 1) частные производные первого
и второго порядка:
.
Найти: 1) частные производные первого
и второго порядка:
![]() ,
2) полные дифференциалы первого порядка
,
2) полные дифференциалы первого порядка![]() и
второго порядка
и
второго порядка![]() ;
;
Решение: Задачу можно решить двумя способами:
способ. Непосредственно найти
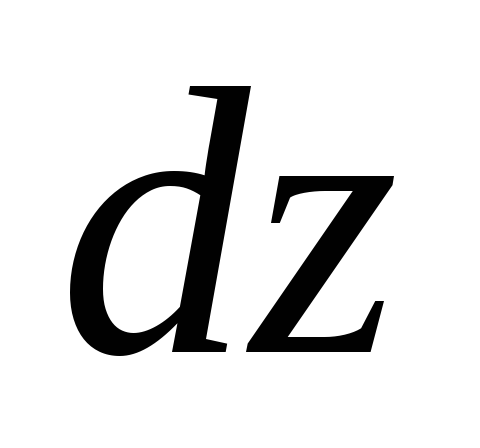 и
и и воспользоваться следующими
соотношениями для дважды дифференцируемых
функций:
и воспользоваться следующими
соотношениями для дважды дифференцируемых
функций:
![]()
![]()
Таким образом,
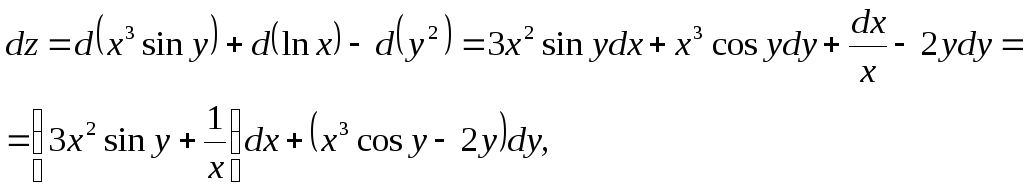
то есть
![]()
![]() .
.
Далее,

То есть
![]()
![]()
![]()
2 способ.
Найдём
частные производные и воспользуемся
соотношениями (1),(2) и (3). Имеем, считая
![]() постоянной:
постоянной:
![]()
![]()
![]()
Аналогично, считая
постоянной
![]()
![]()
![]() ,
,
![]()
![]()
Отметим,
что в силу теоремы о равенстве смешанных
производных у дважды дифференцируемых
функций достаточно было бы найти или
![]() или
или![]()
Получаем:
![]()
![]()
Примеры для самостоятельной работы:
Дана
функция
![]() .
Найти: 1) частные производные первого
и второго порядка:
.
Найти: 1) частные производные первого
и второго порядка:![]() 2)
полные дифференциалы первого порядка
2)
полные дифференциалы первого порядка![]() и
второго порядка
и
второго порядка![]() .
.
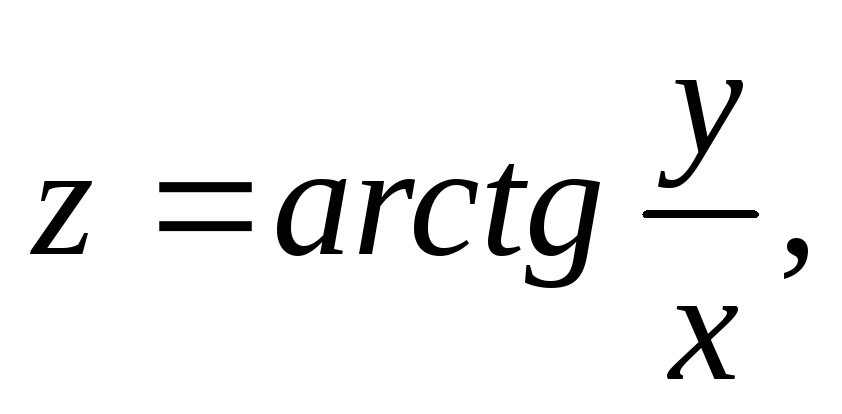

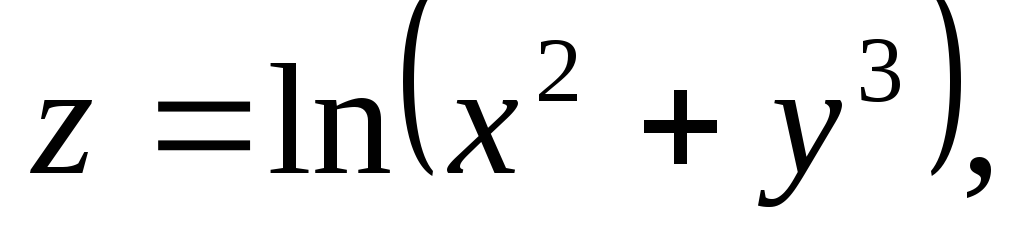
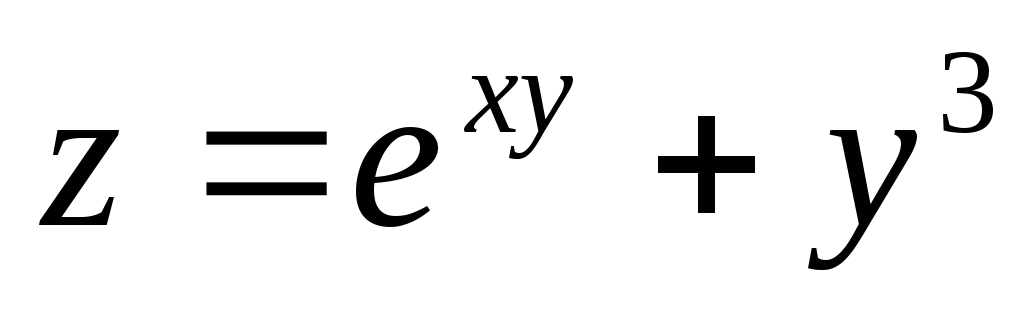
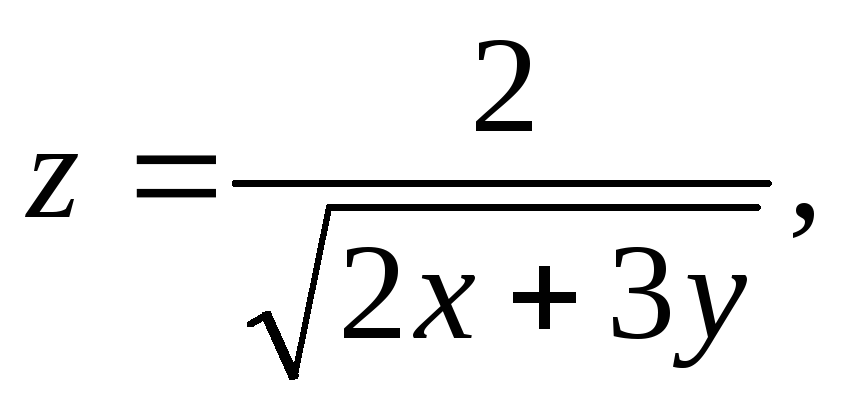
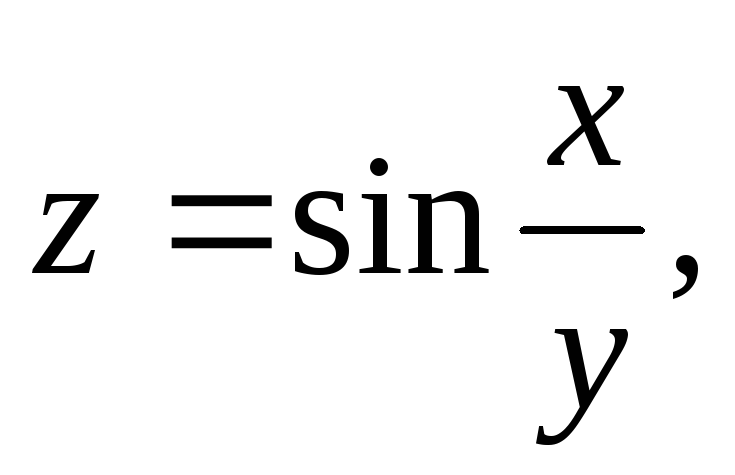
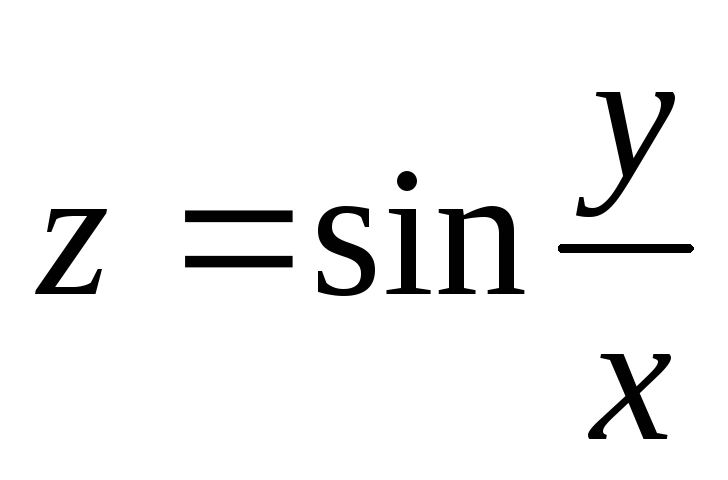 ,
,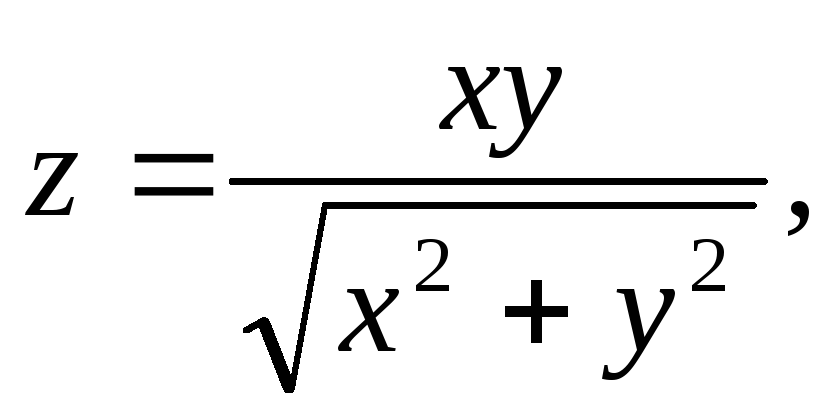
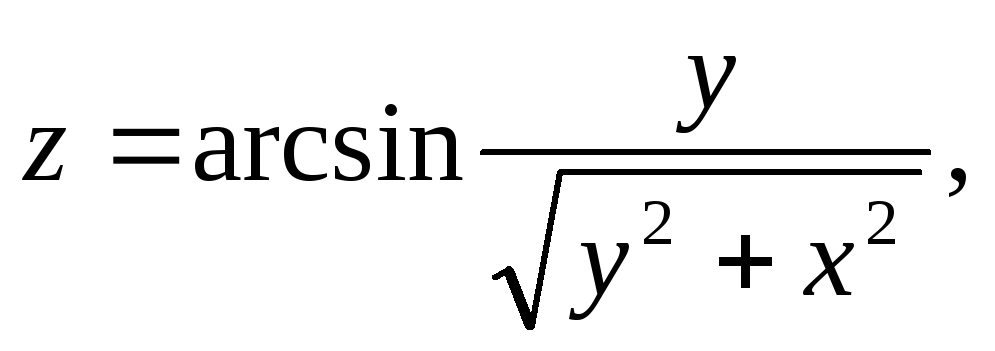
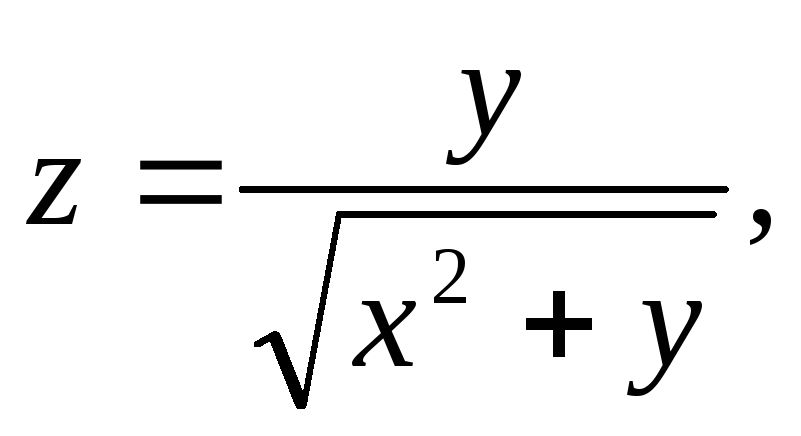
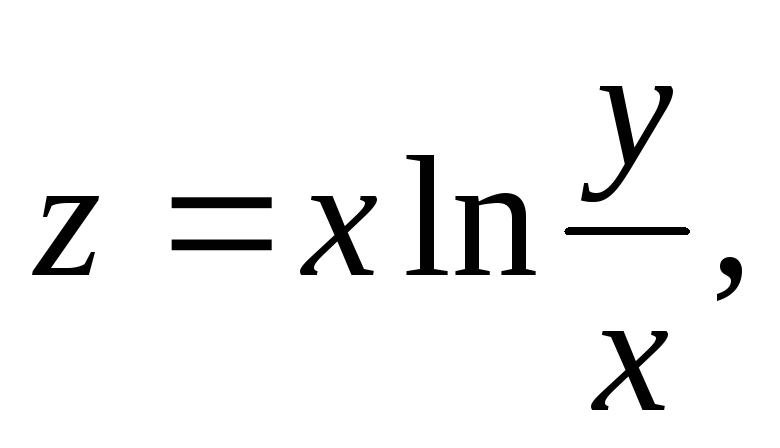
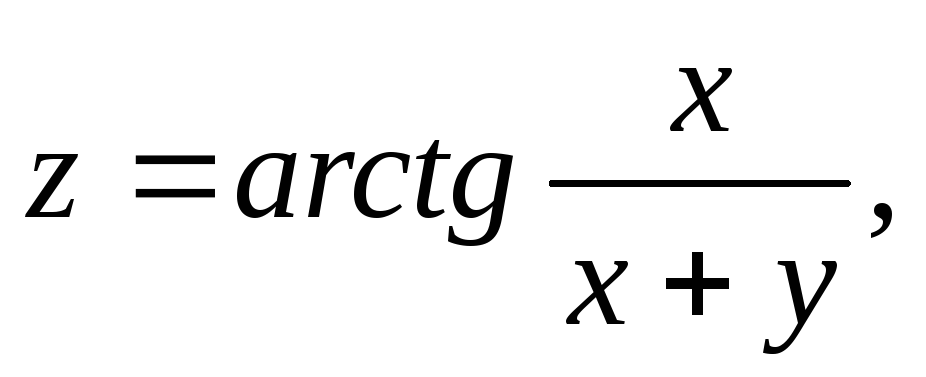
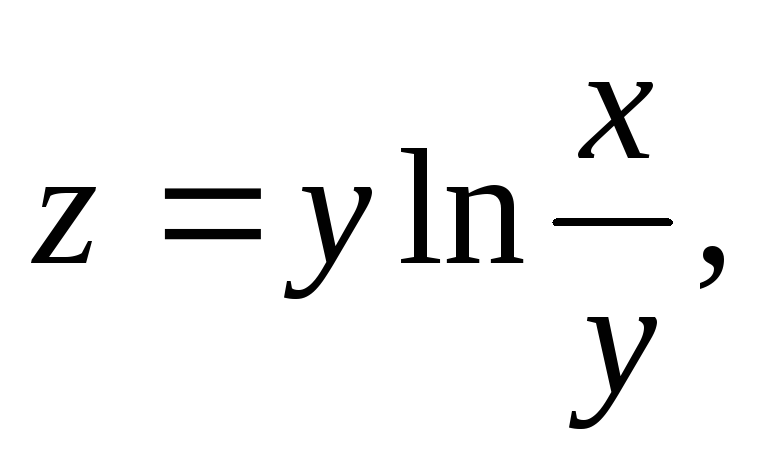
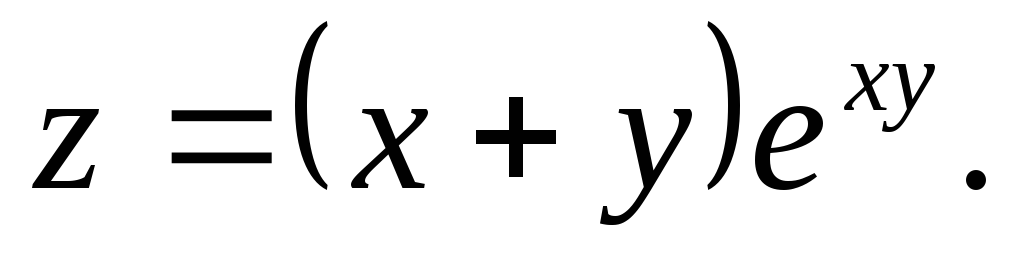
![]() §
3. Использование дифференциала в
приближенных вычислениях.
Пусть дана функция
§
3. Использование дифференциала в
приближенных вычислениях.
Пусть дана функция
![]() и точки
и точки![]() и
и![]() ,
можно найти приближённое значение
данной функции в точке
,
можно найти приближённое значение
данной функции в точке![]() ,
исходя из её точного значения, в точке
,
исходя из её точного значения, в точке![]() заменяя приращение
заменяя приращение![]() дифференциалом
дифференциалом![]() :
:![]()
![]()
![]() (7)
(7)
Пример 3.
Дана
функция
![]() точки
точки![]() Найти приближённое значение данной
функции в точке
Найти приближённое значение данной
функции в точке![]() исходя из её точного значения в
исходя из её точного значения в![]()
Решение:
Применим приближённую формулу, в
предположении, что
![]() достаточно мало
достаточно мало![]() .
.
В
нашем случае
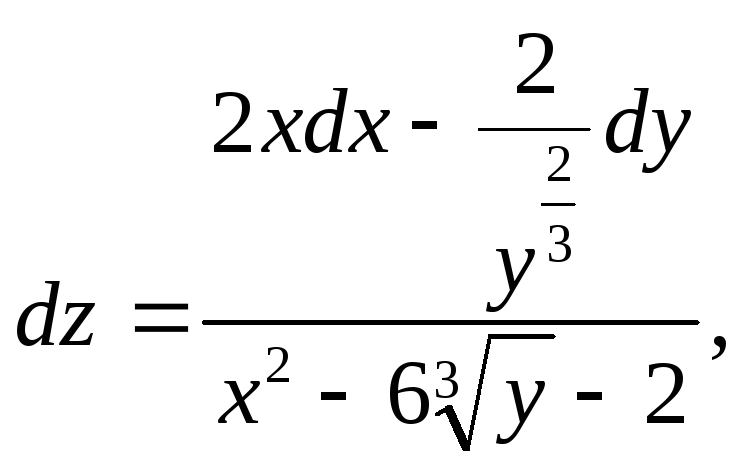 где
где![]()
Тогда
![]() а
а![]()
Следовательно,
![]()
Примеры для самостоятельной работы:
Дана
функция
![]() и точки
и точки![]() и
и![]() .
Найти приближённое значение данной
функции в точке
.
Найти приближённое значение данной
функции в точке![]()
Ответы: 3.1![]() ;
3.2
;
3.2![]() ;
3.3
;
3.3![]() ;
3.4
;
3.4![]() ;
3.5
;
3.5![]() ;
3.6
;
3.6![]() ;
3.7
;
3.7![]() ;3.8
;3.8
