6.3. Применение интегралов для решения количественных медицинских задач

Задача 1За первые 13 дней химиотерапии масса злокачественного новообразования уменьшалась со скоростьюграмм в день.

Какова масса опухоли на десятый день лечения, если начальная ее масса равнялась 180 грамм?

Решение

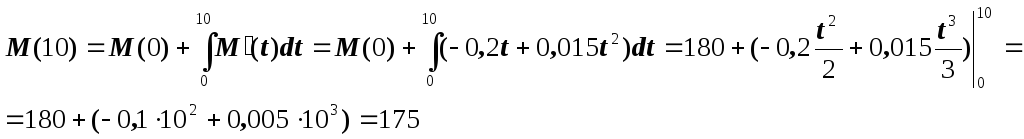
Ответ: 175 грамм.

Задача 2 Количество миллиграмм тетрациклина m(t), поступающее в кровоток черезt минут после приема таблетки определяется скоростью его поступления. Какое количество тетрациклина окажется в крови через 15 минут после приема, если скорость его поступления подчиняется законумг/мин.?

Решение Проводим интегрирование по частям. Положим u=3t, , тогда du=3dt, а . Используя фомулу , решим нашу задачу.

Ответ 18,2мг

7. Дифференциальные уравнения. Введение. Постановка задачи

Очень часто при решении физических задач мы не можем непосредственно установить характер зависимости yот x, но можем установить зависимость междуx,yи производными отyпо x: y, y...y ⁿ.

Рассмотрим это на примере закона радиоактивного распада элементов.

Известно, что атомы радиоактивных элементов с течением времени распадаются. Экспериментально было установлено, что скорость распада атомов пропорциональна числу нераспавшихся атомов в данный момент времени, т.е., если

N -число нераспавшихся атомов в момент времениt,то

.

Чтобы эту запись превратить в равенство, необходимо ввести константу пропорциональности. Обозначим эту константу . Обычно этой буквой обозначается постоянная радиоактивного распада, которая является характеристикой радиоактивного элемента.

Тогда имеем уравнение вида:

(1)

Примечание: знак минус обусловлен тем, что число нераспавшихся атомов с течением времени уменьшается.

Итак, мы получили соотношение (1),связывающее неизвестную функцию N и ее производную, т.е., мы имеем дифференциальное уравнение.

Определение 10. Дифференциальным уравнениемназывается уравнение, связывающее независимую переменнуюx, искомую функциюy = f (x) и ее производнуюy, y ... yⁿ.

Символически дифференциальное уравнение можно написать так:

Определение 11. Порядкомдифференциального уравнения называется порядок наивысшей производной, входящей в уравнение.

Например: y- 2 xy² + 5 = 0 есть дифференциальное уравнение первого порядка,

y + y - by - sin x =0 - дифференциальное уравнение второго порядка.

Определение 12. Решениемилиинтеграломдифференциального уравнения называется всякая функцияy = f (x), которая, будучи подставлена в уравнение, превращает его в тождество.

Следовательно, решить дифференциальное уравнение - это значит найти такую функцию, y = f (x), которая тождественно удовлетворяет данному дифференциальному уравнению.

Таким образом, чтобы решить наше дифференциальное уравнение (1) необходимо найти функцию . Решение этого уравнения приведено ниже.

7.1. Дифференциальные уравнения первого порядка (общие понятия)

Дифференциальным уравнением первого порядка называется уравнение, связывающее независимую переменную, искомую функцию и производную этой функции. Дифференциальное уравнение первого порядка имеет вид:

F(x, y, y )=0

Условия, заключающиеся в том, что при заданных значениях аргумента значения функции или ее производной должны равняться конкретному числу, называются начальными условиями.

Начальные условия можно записать следующим образом:

y = y₀ при x = x₀ или y|_x=x0 = y₀.

Рассматривая выше распад радиоактивного элемента, мы получили дифференциальное уравнение первого порядка

(1)

т.е. F( t, N, N )=0

Попробуем решить это уравнение. Разделим переменные. Уравнение (1) тогда будет иметь вид:

Проинтегрируем это выражение.

(1а)

Замечание: Имея ввиду дальнейшие преобразования, мы обозначили произвольную постоянную через ln C, что вполне допустимо, т.к.ln C(приC0) может принимать любые значения от -до +.

С полученным выражением (1а) проведем несложные алгебраические преобразования

(2)

Нетрудно проверить, что полученная функция (2) удовлетворяет уравнению (1), каково бы ни было постоянное число C.

Следовательно,данная совокупность функцийN = f (t), является решением дифференциального уравнения.

Определение 13. Общим решениемдифференциального уравнения первого порядка называется функция y = (x, C), которая зависит от произвольного постоянногоC и удовлетворяет следующим условиям

1. обращает в тождество дифференциальное уравнение при любом конкретном C;

2. каковы бы ни были начальные условия y = y₀ при x = x₀ можно найти такое значениеC=C₀, что функция y = (x, C₀) удовлетворяет данным начальным условиям.

Рассмотрим далее наш пример. Зададим начальные условия, в момент t = 0- т.е. начало радиоактивного распада, число нераспавшихся атомов былоN=N₀ . Тогда легко можно найти величинуC = C₀, соответствующую данным начальным условиям. Подставляя в выражение (2) вместоN, N₀, а вместо t нуль, имеем

Таким образом, число нераспавшихся атомов зависит от времени по следующему закону

Это выражение есть частное решение дифференциального уравнения.

Определение14. Частным решениемдифференциального уравнения называется любая функцияy = (x, C₀), которая получается из общего решения y = (x, C), если произвольному постоянному C придать определенное значение C=C₀.

Итак, решить дифференциальное уравнение - значит:

1. Найти его общее решение или общий интеграл (если начальные условия не заданы).

2. Найти то частное решение, которое удовлетворяет заданным начальным условиям (если таковые имеются).