2. Логарифмы и их свойства

Логарифмом числа N по основаниюаназывается показатель степених, в которую нужно возвестиа, чтобы получить числоN

, при условии, что ,,

Из определения логарифма следует, что , т.е. - это равенство является основным логарифмическим тождеством.

Логарифмы по основанию 10 называются десятичными логарифмами. Вместо пишут.

Логарифмы по основанию e называются натуральными и обозначаются.

Основные свойства логарифмов.

1. Логарифм единицы при любом основании равен нулю

2. Логарифм произведения равен сумме логарифмов сомножителей.

3) Логарифм частного равен разности логарифмов

4. Логарифм степени равен логарифму модуля основания, умноженному на показатель степени.

5. Логарифм корня равен логарифму модуля подкоренного выражения, деленному на множитель корня.

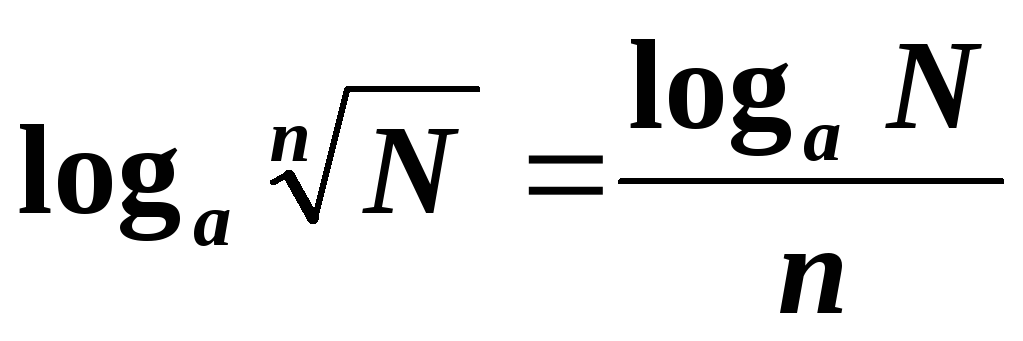
6. Зависимость между логарифмами с различными основаниями определяется формулой.

Множитель называется модулем перехода от логарифмов при основанииa к логарифмам при основанииb.

С помощью свойств 2-5 часто удается свести логарифм сложного выражения к результату простых арифметических действий над логарифмами.

Например,

Такие преобразования логарифма называются логарифмированием. Преобразования обратные логарифмированию называются потенцированием.

Глава 2. Элементы высшей математики.

1. Пределы

Пределом функции является конечное число А, если при стремлении xx₀для каждого наперед заданного , найдется такое число , что как только , то .

Функция, имеющая предел, отличается от него на бесконечно малую величину: , где- б.м.в., т.е..

Пример. Рассмотрим функцию .

При стремлении , функцияy стремится к нулю:

1.1. Основные теоремы о пределах.

1. Предел постоянной величины равен этой постоянной величине

.

2. Предел суммы (разности) конечного числа функций равен сумме (разности) пределов этих функций.

.

3. Предел произведения конечного числа функций равен произведению пределов этих функций.

4. Предел частного двух функций равен частному пределов этих функций, если предел знаменателя не равен нулю.

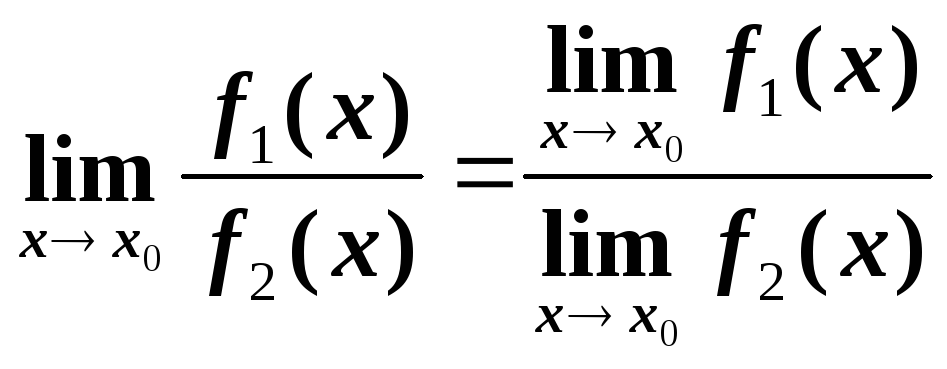
Замечательные пределы

, , где

1.2. Примеры вычисления пределов

Пример 1

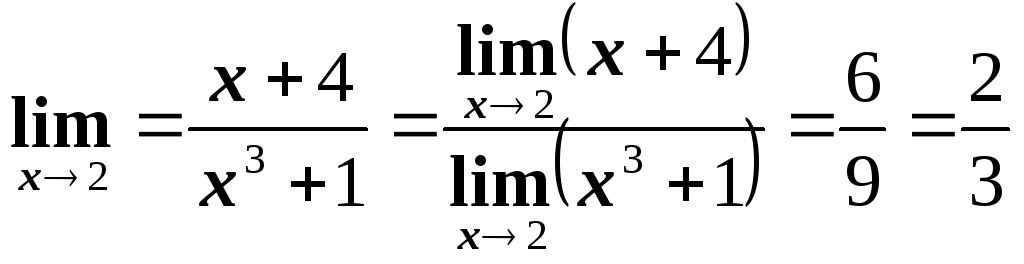
Однако, не все пределы вычисляются так просто. Чаще вычисление предела сводится к раскрытию неопределенности типа: или .

Пример 2

.

Пример 3

.

2. Производная функции

Пусть мы имеем функцию , непрерывную на отрезке .

Аргумент получил некоторое приращение . Тогда и функция получит приращение .

Значению аргумента соответствует значение функции .

Значению аргумента соответствует значение функции .

Следовательно, .

Найдем предел этого отношения при . Если этот предел существует, то он называется производной данной функции.

Определение 3Производной данной функции по аргументу называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента произвольным образом стремится к нулю.

Производная функцииможет быть обозначена следующим образом:

; ; ; .

Определение 4Операция нахождения производной от функции называетсядифференцированием.

2.1. Механический смысл производной.

Рассмотрим прямолинейное движение некоторого твердого тела или материальной точки.

Пусть в некоторый момент времени движущаяся точка находилась на расстоянии от начального положения .

Через некоторый промежуток времени она переместилась на расстояние . Отношение =- средняя скорость материальной точки . Найдем предел этого отношения, учитывая что .

Следовательно, определение мгновенной скорости движения материальной точки сводится к нахождению производной от пути по времени.

2.2. Геометрическое значение производной

Пусть у нас есть графически заданная некоторая функция .

Рис. 1. Геометрический смысл производной

Если , то точка, будет перемещаться по кривой, приближаясь к точке .

Следовательно , т.е. значение производной при данном значении аргумента численно равняется тангенсу угла образованного касательной в данной точке с положительным направлением оси .

2.3. Таблица основных формул дифференцирования.

Степенная функция

Показательная функция

Логарифмическая функция

Тригонометрическая функция

Обратная тригонометрическая функция

2.4. Правила дифференцирования.

Производная от

Производная суммы (разности) функций

Производная произведения двух функций

Производная частного двух функций

2.5. Производная от сложной функции.

Пусть дана функция такая, что ее можно представить в виде

и, где переменнаяявляется промежуточным аргументом, тогда

Производная сложной функции равна произведению производной данной функции по промежуточному аргументу на производную промежуточного аргумента по x.

Пример1.

Пример2.

3. Дифференциал функции.

Пусть есть , дифференцируемая на некотором отрезкеи пустьу этой функции есть производная

,

тогда можно записать

(1),

где - бесконечно малая величина,

так как при

Умножая все члены равенства (1) на имеем:

, где - б.м.в. высшего порядка.

Величина называется дифференциалом функциии обозначается

.

3.1. Геометрическое значение дифференциала.

Пусть дана функция .

Рис.2. Геометрический смысл дифференциала.

.

Очевидно, что дифференциал функции равен приращению ординаты касательной в данной точке.

3.2. Производные и дифференциалы различных порядков.

Если есть , тогданазывается первой производной.

Производная от первой производной называется производной второго порядка и записывается .

Производной n-го порядка от функцииназывается производная (n-1)-го порядка и записывается:

.

Дифференциал от дифференциала функции называется вторым дифференциалом или дифференциалом второго порядка.

. .

3.3 Решение биологических задач с применением дифференцирования.

Задача1. Исследования показали, что рост колонии микроорганизмов подчиняется закону, гдеN– численность микроорганизмов (в тыс.),t–время (дни).

а) Рассчитать численность популяции через 7 дней от посева.

б) Будет ли в этот период численность колонии увеличиваться или уменьшаться?

Решение

а)

б)

Ответ. Численность колонии будет увеличиваться.

Задача 2. Вода в озере периодически тестируется для контроля содержания болезнетворных бактерий. Черезtдней после тестирования концентрация бактерий определяется соотношением

.

Когда в озере наступит минимальная концентрация бактерий и можно будет в нем купаться?

РешениеФункция достигает max или min, когда ее производная равна нулю.

,

Определим max или min будет через 6 дней. Для этого возьмем вторую производную.

Ответ: Через 6 дней будет минимальная концентрация бактерий.