Справочник школьника по математике. 5-11 кл_Маслова Т.Н, Суходский А.М_2008 -672с

Геометрия

7) Площадь треугольника, построенного на векто-

ðàõ a è b, равна половине модуля векторного про-

изведения a íà b.

Отношение периметров и площадей подобных треугольников: если D ABC ~ D A1B1C1 (ðèñ. 316), òî

Ðèñ. 316

2. Прямоугольный треугольник

Обозначения (ðèñ 317):

C = 90°;

a, b — катеты;

565

ОСНОВНЫЕ ФОРМУЛЫ

Ðèñ. 317

ñ — гипотенуза;

h — высота, проведенная из вершины Ñ;

ac,bc — длины отрезков, отсекаемых высотой на гипотенузе.

Теорема Пифагора:

c2 = a2 + b2.

Радиус описанной окружности:

R = 0,5c.

Радиус вписанной окружности: r = 0,5 (a + b - c).

Формулы для площади:

S = 0,5 ab; S = 0,5 ch.

566

Геометрия

3.Правильный треугольник

(à — сторона; рис. 318)

Радиус описанной окружности:

R = a33 .

Ðèñ. 318

Радиус вписанной окружности:

r = a63 .

Высота:

h = a23 . Формулы для площади:

S = a2 3 ; S = 3R2 3 ; S = 3 3r2. 4 4

567

ОСНОВНЫЕ ФОРМУЛЫ

4. Произвольный выпуклый четырехугольник

Сумма углов:

A + B + C + D = 360°.

Площадь:

S = 0,5 d1d2 sin j,

ãäå d1 è d2 — диагонали, j — угол между ними.

Ðèñ. 319

5. Четырехугольник, вписанный в окружность

(ðèñ. 320)

Суммы противоположных углов равны 180°:

A + C = B + D = 180°.

Произведения отрезков, на которые диагонали разбиваются точкой пересечения, равны:

AF × FC = BF × FD.

Теорема Птолемея: произведение диагоналей равно сумме произведений противоположных сторон:

AC × BD = AB × CD + BC × AD.

568

Геометрия

Ðèñ. 320

Площадь:

S = (p - a) (p - b) (p - c) (p - d),

ãäå a, b, c, d — стороны, p = 0,5(a + b + c + d) — полупериметр.

6. Четырехугольник, описанный около окружности (ðèñ. 321)

Суммы длин противоположных сторон равны:

AB + CD = BC + AD.

Ðèñ. 321

569

ОСНОВНЫЕ ФОРМУЛЫ

Площадь:

S = pr,

ãäå ð — полупериметр, r — радиус вписанной окружности.

7. Параллелограмм

Обозначения:

a, b — стороны;

a, b — углы, прилежащие к одной стороне; ha, hb — высоты;

d1, d2 — диагонали;

j — угол между диагоналями.

Сумма углов, прилежащих к одной стороне, равна 180° (рис. 322):

a + b = 180°.

Ðèñ. 322

570

Геометрия

Диагонали в точке пересечения делятся пополам (рис. 322):

AO = OC = 0,5d1, BO = OD = 0,5 d2.

Сумма квадратов диагоналей равна сумме квадратов сторон:

d12 + d22 = 2 (a2 + b2).

Формулы для площади:

1)S = aha = bhb (ðèñ. 323).

2)S = ab sin a (ðèñ. 322).

3)S = 0,5 d1d2 sinj (ðèñ. 324).

Ðèñ. 323

Ðèñ. 324

571

ОСНОВНЫЕ ФОРМУЛЫ

4) Площадь параллелограмма, построенного на век-

торах a è b, равен модулю векторного произведения a íà b.

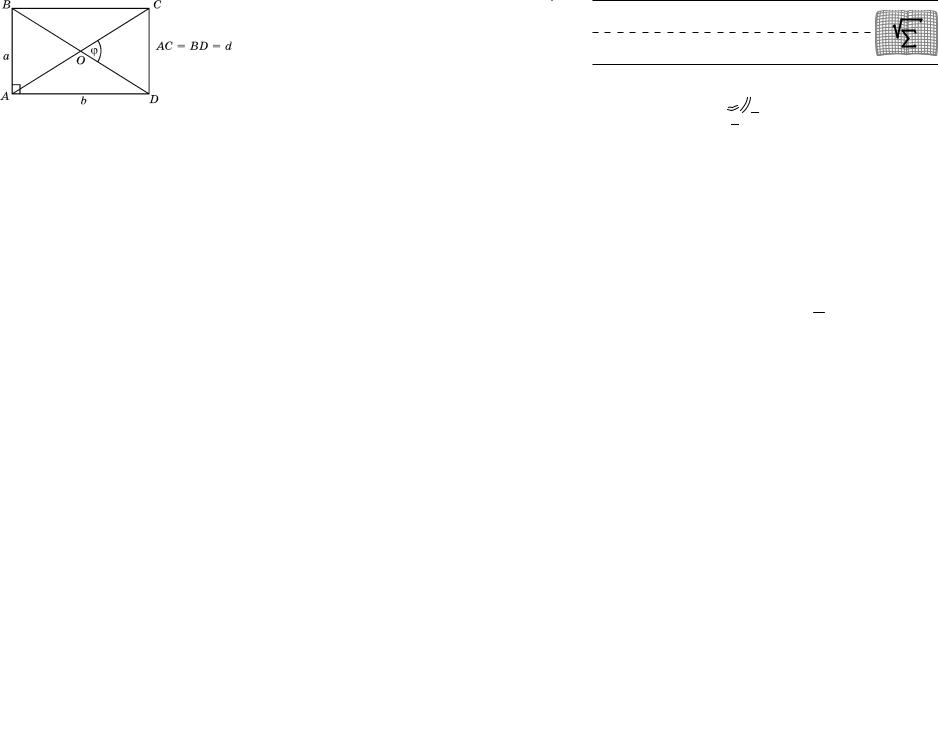
8. Прямоугольник (ðèñ. 325)

Диагонали прямоугольника равны: AC = BD = d. Связь между сторонами и диагональю:

d2 = a2 + b2 .

Ðèñ. 325

Формулы для площади:

S= ab; S = 0,5 d2 sin j.

9.Ðîìá (à — сторона; рис. 326)

Диагонали ромба взаимно перпендикулярны: d1 ^ d2.

572

Геометрия

β

β 2

2

Ðèñ. 326

Диагонали ромба являются биссектрисами его углов:

ÐBAO = ÐDAO = a2 ;

ÐABO = ÐCBO = b2 . Связь между стороной и диагоналями:

d12 + d22 = 4a2.

Формулы для площади:

1)S = aha.

2)S = a2 sin a.

3)S = 0,5 d1d2.

10. Квадрат (à — сторона; рис. 327)

Диагонали квадрата равны и взаимно перпендикулярны: d1 = d2= d, d1 ^ d2.

573

ОСНОВНЫЕ ФОРМУЛЫ

Ðèñ. 327

Связь между стороной и диагональю:

d = a 2.

Формулы для площади:

S = a2; S = 0,5 d2.

11. Трапеция

Обозначения (ðèñ. 328): a, b — основания;

l — средняя линия; h — высота;

d1, d2 — диагонали;

j — угол между ними.

Сумма углов, прилежащих к каждой из боковых сторон ÀÂ è CD, равна 180°:

ÐDAB + ÐABC = 180°; ÐBCD + ÐADC = 180°.

574