Материальный баланс
Система уравнений материального баланса ректификационной колонны:
Массовые расходы исходной смеси, дистиллята и кубовой жидкости:
;
;
.
Молярные массы компонентов [2, с.13]:
легколетучего (бензола) –
.
высококипящего (толуола) –
.
Мольная доля легколетучего компонента в исходной смеси:
.
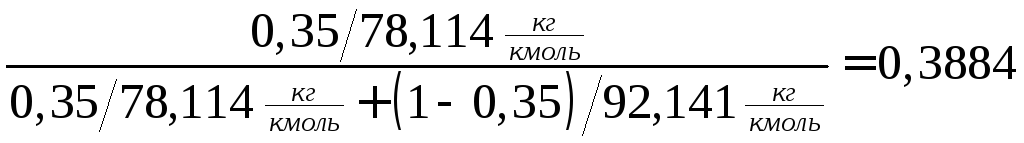Мольная доля легколетучего компонента в дистилляте:
.
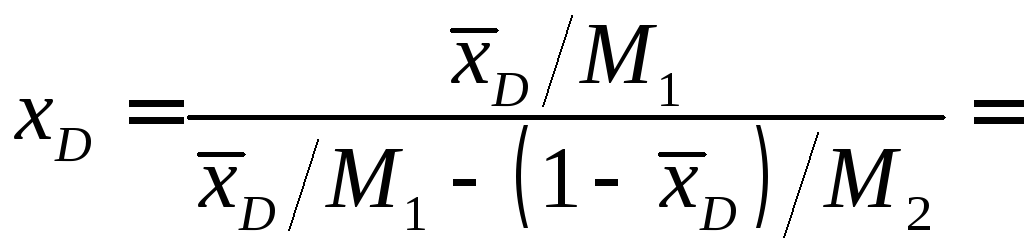
Мольная доля легколетучего компонента в кубовой жидкости:
.
Молярные массы потоков:
исходной смеси
;
дистиллята
;
кубовой жидкости
.
Молярные расходы потоков:
исходной смеси:
;
дистиллята:
;
куб. жидкости:
.
Таблица 1. Материальный баланс ректификационной колонны
|
Поток |
|
|
|
x |
ML | ||
|
т/ч |
кг/с |
кмоль/с |
кмоль/ч |
масс. доли |
мол. доли |
кг/кмоль | |
|
Кубовая жидкость W |
11,78 |
3,271 |
0,03561 |
128,2 |
0,0170 |
0,0200 |
91,86 |
|
Исходная смесь F |
18,00 |
5,000 |
0,05768 |
207,6 |
0,3500 |
0,3884 |
86,69 |
|
Дистиллят D |
6,22 |
1,729 |
0,02207 |
79,4 |
0,9800 |
0,9830 |
78,35 |
Определение минимального флегмового числа
Данные по парожидкостному равновесию для системы бензол-толуол взяты из [2, с. 783-785] таблицы №1453, 1454, 1457, 1458 (давление 760 мм. рт. ст.).
Равновесный состав жидкости на тарелке
питания в случае подачи в колонну
исходной смеси, нагретой до температуры
кипения (вертикальное положение линии
питания), равен составу исходной смеси:
.
Равновесный состав пара на тарелке питания определяется по линии равновесия (графически или линейной интерполяцией по табличным данным):
.
Минимальное флегмовое число:
.
Определение оптимального флегмового числа
Определение оптимального флегмового
числа производится методом итераций.
Задаём начальное значение коэффициента
избытка флегмы
и итерационный шаг
.
Оптимальным флегмовым числом считаем
флегмовое число, соответствующее
минимальному объёму ректификационной
колонны. Поскольку высота колонны
пропорциональна числу теоретических
ступеней (тарелок)
,
а площадь сечения колонны пропорциональна
флегмовому числу плюс единица
,
то объём колонны, равный произведению
площади сечения на высоту, пропорционален
произведению этих величин
.
Таким образом коэффициент оптимизации
.
Первая итерация
Коэффициент избытка флегмы:
.
Флегмовое число:
.
Число теоретических ступеней (тарелок)
находим по x-yдиаграмме, предварительно построив
рабочие линии, соответствующие флегмовому
числу данной итерации:
(см. Приложение, с.??).
Коэффициент оптимизации:
.
Вторая итерация
Коэффициент избытка флегмы:
.
Флегмовое число:
.
Число теоретических ступеней:
(см. Приложение, с.??).
Коэффициент оптимизации:
.
Таблица 3. Определение оптимального флегмового числа
|
№ итерации |
Коэф. избытка флегмы β |
Флегмовое число R |
Число теор. ступеней NТТ |
Коэф. опти-мизации k |
|
1 |
1,20 |
2,111 |
19,9 |
61,9 |
|
2 |
1,25 |
2,199 |
18,8 |
60,1 |
|
3 |
1,30 |
2,287 |
18,0 |
59,3 |
|
4 |
1,35 |
2,375 |
17,4 |
58,7 |
|
5 |
1,40 |
2,463 |
16,8 |
58,1 |
|
6 |
1,45 |
2,551 |
16,4 |
58,1 |
|
7 |
1,50 |
2,639 |
16,0 |
58,2 |
|
8 |
1,55 |
2,726 |
15,7 |
58,5 |
|
9 |
1,60 |
2,814 |
15,4 |
58,6 |
|
10 |
1,65 |
2,902 |
15,0 |
58,7 |
|
11 |
1,70 |
2,990 |
14,7 |
58,7 |
Рис.
6. Определение минимума коэффициента
оптимизации k=NTT·(R+1)