
Reactive Intermediate Chemistry
.pdf274 SINGLET CARBENES
1. INTRODUCTION
1.1. Prototypal Reactions: Addition and Insertion Reactions
Nearly 50 years ago Doering et al.1a and Dvoretzky et al.1b demonstrated the utterly unselective nature of the carbon–hydrogen insertion reactions of methylene, Hine2 elucidated the intermediacy of dichlorocarbene in the hydrolysis of chloroform, and Doering and Hoffmann found that CCl2 could be captured by alkenes to yield cyclopropanes. These seminal reports initiated a one-half century of vigorous research on the chemistry of carbenes, now described in a myriad of journal articles and reviews, as well as in a more manageable number of monographs. Among the latter are the classic ‘‘first generation’’ contributions of Hine4 and Kirmse,5 the two volume set edited by Moss and Jones,6,7 the mammoth reference work edited by Regitz,8 and more recent edited volumes by Platz,9 Brinker,10–12 and Bertrand.13
In Reactive Intermediate Chemistry, five chapters focus on various aspects of carbene chemistry: the present chapter (Chapter 7), devoted to singlet carbenes, Tomioka’s chapter on triplet carbenes (Chapter 9 in this volume), Doyle’s consideration of synthetic aspects of carbene (and nitrene) chemistry (Chapter 12 in this volume), Bertrand’s essay on stable singlet carbenes (Chapter 8 in this volume), and Shevlin’s discussion of the chemistry of atomic carbon (Chapter 10 in this volume). A major theme throughout is the impact of new methods, especially the direct observation of carbenes and high-level computation of their structures and energetics. Over the past 20 years, these techniques have provided increasingly detailed and quantitatively precise mechanisms for the reactions of carbenes and, indeed, reactive intermediates in general. In the specific area of singlet carbene chemistry, we largely focus our discussion on three prototypal carbene reactions: the intermolecular carbene–alkene addition reaction, and the intermolecular and intramolecular insertion reactions. In the discussion there will be some necessary ‘‘leakage’’ of triplet carbene chemistry in order to make comparisons.
1.2. Structure and Bonding
The simple formulation of a carbene as :CR2 hides much of what has fascinated chemists about carbenes for the last five decades. The idea that a molecule as simple as :CH2 can be interesting structurally is deliciously oxymoronic! What is there to say about a three-atom molecule such as methylene? The answer to that question is not only far more complex than it appears on the surface, but the developing of the experimental and theoretical answers has provided an instructive back and forth that showed many of the limitations of both experiment and theory. With the aid of hindsight, one can use the unraveling of the structure of methylene as an exemplar of why it is the cooperative application of theory and experiment that best advances our knowledge.
Let’s start with those two nonbonding electrons. First of all, they can be either paired (singlet state) or unpaired (triplet state). For both singlet and triplet, we need first to know what orbitals contain those electrons. Of course, this first question has
INTRODUCTION 275
a geometric component—before we can explore the ‘‘where’’ question, we have to know what’s possible and the answer to that question depends on geometry. Now the simplicity of the system helps—three points determine a plane and so the geometry question for methylene (and by extension for many other carbenes) quickly devolves to ‘‘linear or bent?’’ We will start with the simpler linear system, build a qualitative molecular orbital (MO) picture, and then bend those orbitals to get the angular system. Finally, we will have to see what theory says about the relative energies of these two forms for both the paired (singlet) and unpaired electron (triplet) cases.
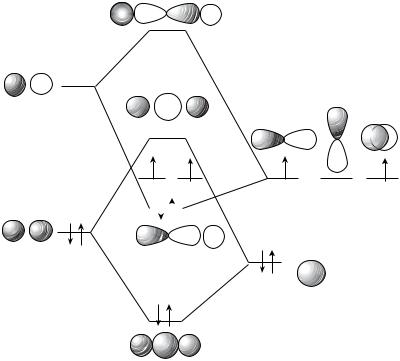
The raw material consists of the atomic orbitals of carbon, 2s, 2px, 2py and 2pz, and the bonding and antibonding MOs of hydrogen, B and A. Considerations of energy and symmetry lead to the interactions shown in Figure 7.1. The interactionsB 2s, and A 2px give four of the six molecular orbitals of linear methylene.
H — C— H
ΨΑ – 2 px = D
H— H
C
ΨA
Ψ Β – 2 s = C
2py |
2pz |
2px |
2py |
2pz |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ψ B |
ΨΑ + 2px = B |
2 s
Ψ Β + 2s = A
Figure 7.1

276 SINGLET CARBENES
The remaining two are the unchanged 2py and 2pz orbitals. There are six electrons to be placed in these orbitals, and for the linear structure, the lowest two, A and B, will be filled, and the 2py, and 2pz will have a single electron each. Hund’s rule suggests that the triplet state with parallel spins will be lower in energy than the singlet state (Fig. 7.1). For an related, alternative valence-shell electron-pair repulsion (VESPR) theory treatment see Chapter 11 by Platz in this volume.
What happens to these orbitals as we deform the linear structure to construct the bent form (Fig. 7.2)? In two orbitals, A and C, a new bonding interaction develops
C
H C H
H H
H
D
C
G
2pz |
2 py |
2pz |
J
F
B
A
E
Figure 7.2

INTRODUCTION 277
on bending to give E and G, and these orbitals will drop in energy as compared to the linear arrangement. In two others, B and D, a new antibonding interaction appears and these orbitals will rise in energy on bending to produce F and H. The 2pz orbital is orthogonal to the plane determined by the three atoms and will not change in energy on bending. It is the last orbital, the 2py, that is the most interesting, because it drops in energy on bending as it gains s character in J. Thus, the pattern of orbitals for a bent species is as shown in Figure 7.2.
Now we need to answer two questions: Where do the electrons go, and which spin state is lower for the bent carbene, singlet or triplet? There is a trade-off between orbital energy and electron–electron correlation (basically repulsion) between the possibilities shown in Figure 7.3. The lowest singlet (1) is surely the bent structure with the three lowest energy MOs filled, and the lowest triplet will have one electron in the thirdand fourth-highest energy orbitals as in linear 2 or bent 3. We now need to decide whether 2 or 3 is lower in energy, and, having done that, decide whether the ‘‘winner’’ is higher or lower than the lowest singlet (1). These are not easy questions to answer! Indeed, the chemical world argued for some decades over them. Finally, it became clear from increasingly sophisticated theoretical and experimental work that, at least for methylene the bent triplet (3) was the overall minimum, with a H C H angle of 137 . The bent singlet state (2) lies some 9 kcal/mol higher, and the H C H angle has decreased to 102 .14 Nature has ‘‘chosen’’ to compromise, gaining some measure of the stabilization afforded by the lowering of orbital energy, while keeping the electrons farther apart than in a singlet state (Fig. 7.3). In addition, in the linear triplet the
Energy
|
|
|
|
|
|
|
|
|
|
|
|
H |
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
H |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
G |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
J |
|
|
|
|
|
|
|
|
|
|
2pz |
2py |
|
|
|
|
2pz |
J |
|
2pz |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
E |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Bent singlet |
|
|
Linear triplet |
|
|
|
Bent triplet |
||||||||||||||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
|
|
||||||||||||||||
Figure 7.3

278 SINGLET CARBENES
carbon–hydrogen bonds have more s character than in a bent arrangement, and are therefore stronger.
Of course, for carbenes more complex than methylene we will have to revisit these questions, and, as the competition between spin states is a close one, we can expect a good deal of variation in the answers for simple carbenes. For example, alkyl groups such as methyl can help stabilize the singlet through a hyperconjugative interaction with the empty 2p orbital, and sterically demanding groups, for example, phenyl, tert-butyl, or adamantyl, should favor the triplet state by demanding a wide R C R angle. Atoms with nonbonding electrons that can donate those electrons into the empty 2p orbital of a singlet are especially effective at producing ground-state singlets (Fig. 7.4). Difluorocarbene, :CF2, is a classic example, but see Chapter 8 in this volume for a discussion of the extraordinarily stable aminocarbenes and phosphinocarbenes.
H |
|
|
|
|
|
|
C |
C |
|
|
Ad |
F |
C |
H |
|
H |
Ad |
|||
|
|
|
||||
H |
|
|
|
|
F |
|
|
|
|
152° |
|
||
|
|
|
|
|
|
|
Methylcarbene |
|
Ad = 1-Adamantyl |
Difluorocarbene |
|||
Figure 7.4
Table 7.1 summarizes the ground states for a variety of structurally diverse carbene types and Table 7.2 gives a few specific values for the energy difference between singlets and triplets for some common carbenes. As you can see, in many cases the two reactive intermediates are very close in energy.
TABLE 7.1. Ground States for Typical Carbenes
Carbene |
Ground State |
:CH2 |
Triplet |
:CR.. 2 |
Singlet or triplet |
HCCOOR |
Triplet |
:C(COOR)2 |
Triplet |
:C(C6H5)2 |
Triplet |
:CAr.. 2 |
Triplet |
HCC6H5 |
Triplet |
:CX |
Singlet |
.. 2 (X¼F, Cl, Br, I) |
|
HCX |
Singlet |
:C(OR)2 |
Singlet |
:C(NR2)2 |
Singlet |

MORE DETAILED TREATMENTS OF STRUCTURE AND PROTOTYPAL REACTIONS |
279 |
|||
TABLE 7.2. Singlet–Triplet Gaps for a Few Typical Carbenesa |
|
|
||
Carbene |
Singlet–Triplet Gap |
Method |
References |
|
|
|
|
|
|
:CH2 |
9 |
Theory |
14b,15 |
|
|
9 |
Experiment |
16,17,18 |
|
:CHCH3 |
3–5 |
Theory |
19 |
|
:C(CH3)2 |
1.4 |
Theory |
20a |
|
.. |
1.6 |
Theory |
20b |
|
HCC6H5 |
2.5 |
Theory |
21a |
|
|
2.3 |
Experiment |
21b |
|
|
4.3 |
Theory |
22 |
|
:CF2 |
57 |
Experiment |
23 |
|
a In kcal/mol; positive value indicates triplet ground state.
2. MORE DETAILED TREATMENTS OF STRUCTURE AND PROTOTYPAL REACTIONS
2.1. Addition Reactions
2.2.1. Philicity. A principal feature of the carbene–alkene addition reaction
(Scheme 7.1) is the carbene’s ‘‘philicity,’’ that is the electronic character of its selectivity or response to the alkene’s substituents.24–26 Early work of Skell and
Garner27 and Doering and Henderson28 showed that CBr2 and CCl2 preferentially
Scheme 7.1
reacted with more highly alkylated olefins (Fig. 7.5). Thus, these carbenes appeared to be electrophiles and transition states such as 4 were drawn25 to represent p-elec- tron donation from the alkene to the carbene (Fig. 7.5).
At that time, however, it was not possible to measure the absolute rates of carbene additions to alkenes, which were too rapid. Accordingly, relative reactivities
R1 |
+ |
R |
3 |
|
.. |
|
δ |
|
|
||
|
|
|
|
Cl |
|
R2 |
|
R4 |
.. |
.. |
|
|
|
||||
Y |
|
δ− |
|
|
|
X |
|
|
|
|
|
|
4 |
|
|
|
|
.. ..
CCl
..
..
+
..Cl
..
_
.. ..
CCl
..
5
 ..
..
.. |
_ |
.. |
|
Cl |
C |
.. |
|
.. |
|
+
Cl
..
..
Figure 7.5

280 SINGLET CARBENES
(approximately equal to relative rate constants) were determined. Alkenes a and b were allowed to compete for an insufficiency of carbene. From the mole ratio of the corresponding product cyclopropanes, corrected for the mole ratio of the initial alkenes, one obtained the relative reactivity ka=kb of the carbene toward the alkene pair.29
Relative reactivities for the electrophilic carbenes CH3CCl and CCl2 appear in Table 7.3,26,30–33 in which they can be seen to react most rapidly with the most
highly alkylated olefins, ðCH3Þ2C CðCH3Þ2, ðCH3Þ2C CHCH3, less rapidly with disubstituted trans-butene (designated as the ‘‘standard’’ alkene, and assigned krel ¼ 1:00Þ, and least rapidly with such electron-poor olefins as methyl acrylate or acrylonitrile.
TABLE 7.3. Relative Reactivities of Carbenes Toward Alkenesa
Alkene |
CH3CClb |
CCl2c |
CH3OCCld |
C6H5OCCle |
CH3OCCH3 f |
||
|
|
|
|
|
|
|
|
ðCH3 |
Þ2C CðCH3Þ2 |
7.44 |
78.4 |
12.6 |
3.0 |
|
|
ðCH3 |
Þ2C CHCH3 |
4.69 |
|
|
|
2.13 |
|
ðCH3 |
Þ2C CH2 |
1.92 |
4.89 |
5.43 |
7.3 |
2.18 |
|
trans-CH3CH CHCH3 |
1.00 |
1.00 |
1.00 |
1.00 |
1.00 |
||
CH2 |
CHCOOCH3 |
0.078 |
0.060 |
29.7 |
3.7 |
362 |
|
CH2 |
CHCN |
0.074 |
0.047 |
54.6 |
5.5 |
686 |
|
a Data are at 25 C except for CCl2 (80 C). All carbenes were generated from diazirines except CCl2 which was produced by thermolysis of C6H5HgCClBr.
b References 30a,b. c Reference 30b.
d Reference 31.
e Reference 32.
f Reference 33.
We also observe that CCl2 shows greater kinetic discrimination than CH3CCl over the set of substrate alkenes; the fastest/slowest relative reactivity ratios are 1668 for CCl2 and 100 for CH3CCl. This observation accords with simple considerations suggesting that CCl2 is the more stabilized, and therefore less reactive carbene. As an approximately sp2 hybridized singlet carbene with a vacant p orbital and a filled sp2 orbital, CCl2 is stabilized by the Clð3pÞ ! carbeneð2pÞ electron donation qualitatively represented by structure 5 (Fig. 7.5). Clearly, CCl2 will be more stabilized than CH3CCl, in which only one Cl atom is present.
A deeper understanding of carbenic philicity requires a more detailed representation of the addition reaction transition state than that afforded by structure 4.
Early MO calculations furnished structure 6 as representative of the transition state for addition of a singlet carbene to an alkene (Fig. 7.6).34,35
We may redraw 6 as 7a and 7b, in terms of frontier MOs.25,26 Here we emphasize the highest occupied molecular orbital–lowest unoccupied molecular orbital (HOMO–LUMO) interactions that operate in the transition state: 7a depicts the LUMO(carbene)/HOMO(alkene) or p–p interaction; 7b shows the HOMO (carbene)/LUMO(alkene) or s–p* interaction. These formulations are especially

MORE DETAILED TREATMENTS OF STRUCTURE AND PROTOTYPAL REACTIONS |
281 |
Figure 7.6
useful because they lend themselves to calculations of the relevant orbital energies, and transition state structures and energetics.36,37
Interaction 7a features net electron donation from the alkene p orbital (HOMO) to the vacant carbene p orbital (LUMO), and tracks the electrophilic character of the carbene. Interaction 7b represents electron donation from the filled carbene s orbital (HOMO) to the vacant alkene p* orbital (LUMO) and reflects the carbene’s nucleophilic character. Both interactions operate simultaneously in the addition transition state, but which one is dominant?
From the relative reactivities in Table 7.3, we conclude that 7a is dominant for CH3CCl and CCl2, which exhibit electrophilic selectivity toward the alkenes. On the other hand, CH3OCCH3 displays strongly nucleophilic selectivity toward the electron-poor alkenes. Resonance donation from the methoxy oxygen atom to the carbene 2p orbital (8, Fig. 7.7) is sufficiently strong to render CH3OCCH3 a nucleophilic carbene for which s ! p* carbene to alkene electron donation is dominant in the transition state (viz., 7b).
+ –
CH 3O |
|
C |
|
CH 3 |
|
CH3O |
|
C |
|
CH 3 |
|
|
|
|
|
||||||
|
|
|
|
|
8
Figure 7.7
If CCl2 and CH3OCCH3 represent electrophilic and nucleophilic carbenes, respectively, in which the transition states predominantly resemble 7a or 7b, can we identify carbenes for which both p–p and s–p* electronic interactions are comparably important? Such carbenes would react as electrophiles with electron-rich alkenes, but as nucleophiles with electron-poor alkenes; that is, they would be ambiphiles.25 Indeed, Table 7.3 shows that CH3OCCl31 and C6H5OCCl32 behave in just this manner. Their relative reactivities are high toward both electron-rich and electron-poor alkenes, but lower toward alkenes that are electronically ‘‘moderate’’ (trans-butene or 1-hexene26).
Our qualitative discussion has limitations. Why, for example, is CH3OCCH3 seemingly more nucleophilic than CH3OCCl (Table 7.3)? If resonance donation by CH3O (as in 8) makes interaction 7b dominant in the addition reactions of CH3OCCH3, why should additional resonance donation by Cl (as in 5) not make

282 SINGLET CARBENES
CH3OCCl even more nucleophilic? Of course, we have not yet considered inductive effects; Cl is significantly more withdrawing inductively than OCH3, and a more complete treatment must consider this effect. Indeed, empirical correlations of carbene relative reactivities have been developed based on linear free energy treat-
ments that make use of the resonance (sRþ) and inductive (sI ) constants of a carbene’s substituents (X and Y in CXY).24–26,38 These correlations can be
used to predict whether a given carbene should be electrophilic, ambiphilic, or nucleophilic.25
A more precise approach makes use of computational methods. We calculate the carbenic orbital energies36 corresponding to the interactions expressed in 7a and 7b, and evaluate the differential orbital energies for each interaction, Eqs. 1 and 2.26,39
eE ¼ eCXYLU eCHO¼C ¼ p p |
ð1Þ |
eN ¼ eCLU¼C eCXYHO ¼ p s |
ð2Þ |
where LU ¼ LUMO and HO ¼ HOMO |
|
We insert the appropriate orbital energies into Eqs. 1 and 2, in which eE and eN represent the differential orbital energies corresponding to the electrophilic (7a) and
nucleophilic (7b) interactions, respectively. Numerical results for CCl2, CH3OCCl, CH3OCCH3, and (CH3O)2C appear in Table 7.4.24,26
According to frontier MO theory,37 the stabilization energy of a cycloaddition transition state depends inversely on the differential energies of the interacting ‘‘frontier’’ MOs. If we neglect orbital overlap, a smaller e implies greater stabilization, a lower activation energy, and a higher rate constant. Inspection of e for CCl2 in Table 7.4 shows that eE < eN for each alkene substrate. Accordingly, transition state interaction 7a should dominate the addition reactions of CCl2, which should therefore exhibit electrophilic selectivity over the alkene set of Table 7.4. The experimental relative reactivities shown in Table 7.3 agree with this prediction.
TABLE 7.4. Differential Orbital Energies (eV) for Carbene–Alkene Additionsa
|
|
|
CCl2b |
CH3OCClb |
CH3OCCH3b |
(CH3O)2Cb |
||||
|
|
|
—————— |
—————— |
————— |
————— |
||||
Alkene |
eE |
eN |
eE |
eN |
eE |
eN |
eE eN |
|||
|
|
|
|
|
|
|
|
|
|
|
ðCH3 |
Þ2C CðCH3Þ2 |
8.58 |
13.71 |
10.73 |
13.09 |
12.31 |
11.68 |
12.36 |
13.08 |
|
ðCH3 |
Þ2C CHCH3 |
8.99 |
13.68 |
11.14 |
13.06 |
12.72 |
11.65 |
13.02 |
12.86 |
|
ðCH3 |
Þ2C CH2 |
9.55 |
13.63 |
11.70 |
13.01 |
13.28 |
11.60 |
13.33 |
13.00 |
|
trans-CH3CH CHCH3 |
9.43 |
13.54 |
11.58 |
12.92 |
13.16 |
11.51 |
13.21 |
12.91 |
||
CH2 |
CHCOOCH3 |
11.03 |
12.24 |
13.18 |
11.62 |
14.76 |
10.21 |
14.81 |
11.61 |
|
CH2 |
CHCN |
11.23 |
11.65 |
13.38 |
11.03 |
14.96 |
9.62 |
15.01 |
11.02 |
|
a See Eqs. 1 and 2. Orbital energies can be found in Ref. 25, 33, and 36.
b The subscript E in eE ¼ electrophilic. The subscript N in eN ¼ nucleophilic.

MORE DETAILED TREATMENTS OF STRUCTURE AND PROTOTYPAL REACTIONS |
283 |
In contrast, the e values for CH3OCCH3 in Table 7.4 reveal that eN < eE, so that interaction 7b should dominate additions of this carbene. It should be nucleophilic, and Table 7.3 demonstrates that CH3OCCH3 does indeed exhibit pronounced reactivity toward electron-poor alkenes.
Most strikingly, the e values for CH3OCCl in Table 7.4 ‘‘cross-over.’’ For the electron-rich alkenes, eE < eN, whereas eN < eE for the electron-poor alkenes. Here is a clear prediction that CH3OCCl should behave as an ambiphile, reacting rapidly with both electron-rich and electron-poor alkenes, but reacting more slowly with alkenes of modest electronic properties. Again, the relative reactivities of Table 7.3 are consonant with these ideas.
The computed values of eE and eN also predict that dimethoxycarbene should be a nucleophilic carbene. Experimentally, dimethoxycarbene does not add at all to electron-rich alkenes (preferring to dimerize instead), but does add readily to electron-poor methyl acrylate and acrylonitrile.40 Many other nucleophilic reactions of (CH3O)2C and related dialkoxycarbenes have been investigated and reviewed by Warkentin.41
In summary, carbenic electrophilicity is favored by a low-lying HOMO or s orbital, which makes electron donation by the carbene unfavorable, and by a low-lying, accessible LUMO or p acceptor orbital. Conversely, carbenic nucleophilicity is favored by a high-lying HOMO for efficient electron donation, and a high-lying, inaccessible LUMO.24,26 Other quantitative treatments of carbenic philicity appear in the work of Houk and co-workers,36 Schoeller and Brinker,42 Platz and co-workers,43 Zollinger,44 Fukui and co-workers,45 and Garcia-Garibay and coworker.46 Their work is reviewed in Ref. 24, and is in general agreement with the conclusions presented here.
Sander applied DFT (B3LYP) theory to carbenic philicity, computing the electron affinities (EA) and ionization potentials (IP) of the carbenes.47,48 The EA tracks the carbene’s electrophilicity (its ability to accept electron density), whereas the IP represents the carbene’s nucleophilicity (its ability to donate electron density). This approach parallels the differential orbital energy treatment. Both EA and IP can be calculated for any carbene, so Sander was able to analyze the reactivity of ‘‘super’’ electrophilic carbenes such as difluorovinylidene (9)49 which is sufficiently electrophilic to insert into the C H bond of methane. It even reacts with the H H bond of dihydrogen at temperatures as low as 40 K, Scheme 7.2)!
F2C =C + H |
|
H |
|
F2C=CH2 |
|
|
|||
9 |
|
|
|
|
Scheme 7.2
At the opposite end of the philicity spectrum, nucleophilic carbenes have proven useful in synthesis. Warkentin41 pioneered the thermolysis of oxadiazolines as precursors for (CH3O)2C and related dioxacarbenes (Scheme 7.3). Dimethoxycarbene generated from an oxadiazoline undergoes a variety of intermolecular reactions.41 One example is the ring enlargement of strained cyclic ketones, for example, cyclobutanone.50 In this reaction, the nucleophilic carbene initiates the ring expansion by
