Molecular Heterogeneous Catalysis, Wiley (2006), 352729662X

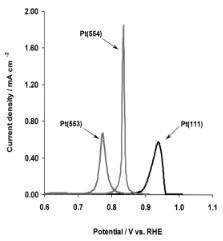
306 Chapter 6

The important di erences between the electrochemical and gas-phase systems are the result of:

(1)direct contributions from the adsorbed liquid phase.

(2)direct activation of the molecule by the aqueous phase protons, leading to the bond cleavage and formation of water without the direct activation of the NO bond by contact with the surface atoms.

6.6 Electrocatalytic Oxidation of CO

The electrochemical reduction of NO discussed in the previous section was found to be independent of surface steps. By way of comparison, we discuss in this final section the electrochemical oxidation of CO which, in contrast, is strongly a ected by the presence of surface steps.

Figure 6.32. The stripping profiles from a saturated CO adlayer over di erent Pt single-crystal surfaces, sweep rate 50 mV/s[65]. CO adlayer oxidation is structure sensitive.

Figure 6.32 compares the voltage at which CO oxidation starts[65] over the Pt(111), Pt(553) and Pt(554) surfaces which contain planar terraces and steps which are 10 or 5 atoms wide, respectively. The steps are oriented in the (110) direction. The overall reaction scheme is

The potential dependence of the apparent rate constant is found to be structure insensitive and gives a Tafel slope of (80 mV)−1, which is consistent with step (6.50) being rate limiting (see Addendum to this chapter).

The reaction preferably takes place at the steps, whereas the terraces supply CO through fast surface di usion. Infrared spectra acquired during he oxidation of the CO

Mechanisms for Aqueous Phase Heterogeneous Catalysis and Electrocatalysis 307

adlayer indicate that CO adsorbed on the (111) terraces is more reactive than that adsorbed on the steps. The infrared frequencies for CO adsorbed on terraces initially declines during course of reaction. CO adsorbed on steps reacts later.

The apparent reaction rates fall in the range 10−2–102 s−1. The oxidative activation of water to form OH groups appears to occur at the step sites. The OH intermediates can subsequently go on to oxidize CO. The intrinsic catalytic reactivity of the steps is shown to be independent of the step density. In the oxidation of a saturated CO adlayer, two processes are distinguished: reaction initiation, which is a zero-order process in which CO desorbs to generate reaction centers, and an oxidation process that is of the Langmuir– Hinshelwood form with competitive adsorption of CO and OH. CO di usion is thought to be fast dCO 10−11 cm2/s) on the terraces towards the step where OH is generated.

Step (6.49) preferably occurs at the step edges and is fast. This implies that OHads builds up concentration at the step edges. The CO binds to strong on step edges to react. The more weakly bonded, mobile CO adsorbed to terrace, therefore, reacts first with adsorbed OH.

6.7 Summary

In previous chapters, we aluded to the importance of solvent e ects on di erent catalytic reactions. More specifically in Section 5.4 we discussed the molecular basis for the di erences that arise between gas-phase and liquid-phase acidity. In this chapter, we provide a further analysis of solvent e ects on surface-catalyzed reactions focusing on the role of protonic solvents such as water on elementary physicochemical steps. An important part of this chapter deals with electrocatalysis. One of the key concepts that arises in both chemical and electrochemical processes carried out in solution is that water (or the solvent) itself can often behave as a co-reactant. For instance, in the gas phase the dissociation of protic reagents such as water or ammonia over a transition-metal surface occurs homolytically, leading to the generation of surface intermediates such as hydroxyl (OH*) or amine (NH2*) fragments along with a surface hydride (H*). In the presence of solution, however, the dissociation can occur heterolytically, thus forming charged products such as OH− and H+ or NH2 − and H+ . The anion fragments tend to transfer their electron to the metal surface whereas the protons that form can be stabilized as hydronium or Zundel ions in solution. The work function of the metal plays an important role in electron capture thus dictating whether or not heterolytic dissociation can occur at least in the absence of an applied potential. The activation of bonds can now proceed without the intermediate adsorption of both the molecular fragments on the surface as we have seen for electrochemical NO reduction. In this system, there is little influence of step sites on the reaction kinetics. NO dissociation instead proceeds first through the protonation of NO by hydronium ions. This weakens the NO bond appreciably and enhances its activation.

Intrinsic to reactions in polar media is the stabilization of the charge separation that forms in the transition state by the large dielectric constant of the medium. The activation barriers for reactions that proceed via the formation of polar transition states are therefore significantly lowered owing to the charge stabilization of the transition state from the polar medium. The charged product intermediates are also stabilized by the solution phase. Low-temperature ammonia oxidation over Pt, for example, occurs heterogeneously in the gas-phase as well as electrocatalytically. In the gas phase, the reaction requires coadsorbed oxygen atoms to be present on the surface in order to help activate the NH bond in ammonia. NH2 and NH species are activated by OHads. On the electrode, the role of

310 Chapter 6

In principle two additional cases can be considered:

A + e B

B −→ C

The electrochemical step at equilibrium, the chemical step first order in surface concentration, gives a Tafel slope of (60 mV)−1. Of the three successive electron transfer steps, two are at equilibrium with Tafel slope (20 mV)−1:

A + e B

B + e C

C + e −→ D

References

1.P.A. Thiel, T.E. Madey, Surf. Sci. Rep. 7, 211 (1987)

2.M.A. Henderson, Surf. Sci. Rep. 46, 1 (2002)

3.(a) S.K. Desai, P. Venkataraman, M. Neurock, J. Phys. Chem. B, 105, 9171 (2001);

(b) S.K. Desai, M. Neurock, unpublished results;

S.K. Desai, M. Neurock, Phys. Rev. B, 68, 075420 (2003)

4.A. Michaelides, A. Alavi, D.A. King J. Am. Chem. Soc. 125, 2746 (2003)

5.A. Michaelides, V.A. Ranea, P.L. de Andres, D.A. King Phys. Rev. Lett. 90, 216102 (2003)

6.P. Vassilev, M.T.M. Koper, R.A. van Santen, Chem. Phys. Lett. 359, 337 (2002)

7.G. Held, D. Menzel, Surf. Sci. 316, 92 (1994);

G. Held, D. Menzel, Phys. Rev. Lett. 74, 4221 (1994);

G. Held, D. Menzel, Surf. Sci. 327, 301 (1995)

8.P.J. Feibelman, Science, 295, 99 (2002)

9.F.T. Wagner, T.E. Moylan, Surf. Sci. 206, 187 (1988)

10.N. Kizhakevariam, E.M. Stuve, Surf. Sci. 275, 223 (1992)

11.M. Neurock, S. Wasileski, unpublished results (2004)

12.C.V. Grotthus, Ann. Chim. Paris, 58, 54 (1815)

13.A.B. Anderson, J. Chem. Phys. 62, 1187 (1975)

14.P.S. Bagus, G. Pacchioni, Electrochim. Acta, 36, 1669 (1991)

15.F. Illas, F. Mele, Electrochim. Acta, 44, 1213 (1998)

16.D.K. Lambert, Electrochim. Acta, 41, 623 (1996)

17.D. Curulla, A. Clotet, Electrochim. Acta, 45, 639 (1999)

18.M. Head-Gordon, J.C. Tully, Chem. Phys. 175, 37 (1993)

19.S.A. Wasileski, M.T.M. Koper, J. Phys. Chem. B, 105, 3518 (2001)

20.(a) A.B. Anderson, D.B. Kang, J. Phys. Chem. A, 102, 5993 (1998);

(b)A.B. Anderson, T.V. Albu Electrochem. Commun. 1, 203 (1999);

(c)A.B. Anderson, T.V. Albu, J. Am. Chem Soc. 121, 11855 (1999);

(d)A.B. Anderson, J. Electrochem. Soc. 147, 4229 (2000);

(e)A.B. Anderson, Electrochim. Acta, 47, 3759 (2002);

Mechanisms for Aqueous Phase Heterogeneous Catalysis and Electrocatalysis 311

(f)A.B. Anderson, N.M. Neshev, Electrochim. Acta, 47, 2999 (2002);

(g)A.B. Anderson, R.A. Sidik, J. Phys. Chem. B, 107, 4618 (2003);

(h)A.B. Anderson, Electrochim. Acta, 48, 3743 (2003)

21.(a) R.A. Marcus, J. Chem. Phys., 43, 679 (1965); (b)R.A. Marcus, J. Electroanal. Chem., 438, 251 (1997)

22.J.W. Halley, A. Mazzolo, J. Electroanal. Chem. 450, 273 (1998)

23.A.Y. Lozovio, A. Alavi, J. Kohano , R.M. Lynden-Bell J. Chem. Phys. 115, 1661 (2001)

24.J.S. Filhol, M. Neurock, in preparation

25.G.Makov, M. Payne, Phys. Rev. B, 51, 4014 (1995)

26.J.F. Janak, Phys. Rev. B, 18, 7165 (1978)

27.E.R. K¨otz, H. Ne , J. Electroanal. Chem. 215, 331 (1986)

28.J.O.M. Bockris, A.K.N. Reddy, Modern Electrochemistry,) Vol. 2A, Kluwer, New York (1998)

29.A. Czerwinski, I. Kiersztyn, J. Electroanal. Chem. 491, 128 (2000); A. Czerwinski, I. Kiersztyn, J. Electroanal. Chem. 471, 190 (1999)

30.J.S. Filhol, M. Neurock, Angew. Chem. Int. Ed. submitted (2005)

31.C. Taylor, S. Wasileski,J. Fanjoy, J.S. Filhol, M. Neurock Phys. Rev. B, submitted (2005)

32.C. Taylor, R. Kelly, M. Neurok, to be submitted (2005)

33.W. Schwerdtel, Hydrocarbon Proc. 47, 187 (1968)

34.C. Reilly, J.J. Lerou, Catal. Today 41, 433 (1998)

35.P. Henry, Catalysis by Metal Complexes: II. Palladium Catalyzed Oxidation of Hydrocarbons, Reidel (ed.), Boston (1980)

36.(a) D.A. Kragten, R.A. van Santen, Inorg. Chem. 38, 331 (1999);

(b)D.A. Kragten, R.A. van Santen, M. Neurock, J.J. Lerou, J. Phys. Chem. A,

103, 2756 (1999)

37.S. Nakamura, T. Yasui, J. Catal. 17, 366 (1970); S. Nakamura, T. Yasui, J. Catal. 23, 315 (1971)

38.I.I. Moiseev, M.N. Vargaftik, Izr. Akad. Nauk. SSSR, Engl. Transl. 133, 377 (1960); I.I. Moiseev, M.N. Vargaftik, in Perspectives in Catalysis, J.M. Thomas, K.I. Zamaraev (eds.), Blackwell Scientific, Oxford, p. 91 (1992)

39.M. Neurock, D.A. Kragten, J. Catal. submitted (2004)

40.B. Samanos, P. Bountry, J. Catal. 23, 19 (1971)

41.S.A.H. Zaidi, Appl. Catal. 38, 353 (1988)

42.M. Tamura, T. Yasui, Kagaku Zasshi, 72, 561 (1969)

43.L.S.J. Campbell, J. Phys. Chem. B, 104, 11168 (2000)

44.P.M. Henry, R.N. Pandey, Homogeneous Catalysis–II. Advances in Chemistry Series

Chicago (1973)

45.D.A. Kragten, Thesis, Eindhoven University of Technology (1999)

46.H. Debellefontaine, J. Besombes-Vailhe, J. Chim. Phys. 75, 801 (1978)

47.S.M. Augustine, J.P. Blitz, J. Catal. 142, 312 (1993)

48.E.A. Crathorne, D. MacGowan, S.R. Morris, A.P. Rawlinson J. Catal. 149, 254 (1994)

49.(a) W.T. Tysoe, D. Stacchiola, J. Am. Chem. Soc. 126, 15384 (2004);

(b) D. Stacchiola, F. Calaza, L. Burkholder, A. Schwabacher, M. Neurock, W. T. Tysoe, Angew. Chem. Int. Ed. 44, 2 (2005)

50.D.A. Hickman, L.D. Schmidt, Ind. Eng. Chem. Res. 30, 50 (1991)

312Chapter 6

51.A. Bogavic, K.C. Hass, Surf. Sci. 546, L237 (2002)

52.(a) L. Kieken, M. Neurock, D. Mei, J. Phys. Chem. B, 109, 2234 (2004);

b) D. Mei, Q. Ge, M. Neurock, L. Kieken, and J. Lerou, Mol. Phys. 102, 361 (2004)

53.M. Neurock, R.A. van Santen, J. Am. Chem. Soc. 116, 4427 (1994)

54.(a) D.P. Sobczyk, A.M. de Jong, E.J.M. Hensen, R.A. van Santen, J. Catal. 219,

156 (2003)

(b) D.P. Sobczyk, A.M. de Jong, E.J.M. Hensen, R.A. van Santen, Top. Catal. 23, 109 (2003)

55.(a) L. Gang, J. van Grondelle, R.A. van Santen, J. Catal. 186, 100 (1999);

(b) L. Gang, J. van Grondelle, R.A. van Santen, J. Catal. 199, 107 (2001)

56.A.C.M. v.d. Broek, J. van Grondelle, R.A. van Santen, J. Catal. 185, 297 (1999)

57.M. Kim, S.J. Pratt, D.A. King, J. Am. Chem. Soc. 122, 2409 (2000)

58.A.C.M. van den Broek, J. van Grondelle, R.A. van Santen, Catal. Lett. 55, 79 (1998);

(b) A.C.M. van den Broek, J. van Grondelle, R.A. van Santen, J. Catal. 167(Iss 2), 147 (1997)

59.S.D. Pell, J.N. Armor, J. Am. Chem. Soc. 97, 5012 (1975); Z. Assefa, D.M. Stanbur, J. Am. Chem. Soc. 119, 521 (1997)

60.S.D. Pell, J.N. Armor, J. Am. Chem. Soc. 94, 686 (1972); S.D. Pell, J.N. Armor, J. Am. Chem. Soc. 95, 7625 (1973); J.D. Buhr, H. Taube, Inorg. Chem. 19, 2425 (1980)

61.W.M.H. Sachtler, Z. Zhang, Adv. Catal. 39, 139 (1993)

62.A.C.A. de Vooys, M.T.M. Koper, R.A. van Santen, J.A.R. van Veen,

J. Electroanal Chem. 506, 127 (2001)

63.A.C.A. de Vooys, M.T.M. Koper, R.A. van Santen, J.A.R. van Veen, J. Catal. 202, 387 (2001)

64.G.L. Beltramo, M.T.M. Koper, Langmuir 19, 8907 (2003)

65.N.P. Lebedeva, M.T.M. Koper, J.M. Feliu, R.A. van Santen, J. Phys. Chem. B, 106, 12938 (2002);

N.P. Lebedeva, A. Rodes, J.M. Feliu, M.T.M. Koper, R.A. van Santen, J. Phys. Chem. B, 106, 9863 (2002)

66.D. Pletcher, F.C. Walsh, Industrial Electrochemistry, Blackie, Glasgow (1993)

67.J.K. Nørskov, J. Rossmeisal, A. Logadottir, L. Lindqvist, J. Kitchin, T. Bligaard, H. Jonsson,J. Phys. Chem. B, 108, 17886 (2004)

CHAPTER 7

Mechanisms in Biocatalysis; Relationship with Chemocatalysis 7.1 General Introduction

In this chapter we summarize key molecular concepts in biocatalysis and compare them with the molecular understanding of reaction mechanisms in heterogeneous catalysis that was developed in the previous chapters. The first four sections of this chapter emphasize enzyme catalysis. Biomimetic approaches are described in later sections.

More specifically we analyze the similarities and di erences between bioand chemocatalytic systems in the sections on oxidation and reduction catalysis. We highlight the important mechanistic concepts and energetic requirements that were described in the previous chapters such as pre-transition-state orientation and solvation (the dielectric constant of an enzyme is as low as that of a zeolite) and the match of the shape and size of the transition state with the enzyme cavity. In this context, it will be important to compare enzyme action concepts such as “lock and key” and “induced fit” with some of the related ideas discussed in Chapter 2. We refer back to concepts in transition-metal surface catalysis in order to establish ideas on possible mechanisms.

The active site of the enzyme is located in a cleft of the peptide framework. The “site” may be considered to be equivalent to that for a homogeneous organometallic catalyst in that it involves a single center with a complex ligand sphere. The results can also be related back to those that occur at metal atom sites on the surface of a metal, metal oxide or metal sulfide. The classical relationship between the conservation of active sites and the turnover of a catalytic cycle suggests that enzyme kinetics should be analogous to those in homogeneous and heterogeneous catalysis.

The Michaelis–Menten rate expression for a monomolecular enzyme-catalyzed reaction is very similar to the Langmuir kinetic expression that we discussed previously for heterogeneous catalyzed systems. The Michaelis–Menten relationship is readily deduced for a simple model where the enzyme molecule (E) equilibrates with substrate molecule (S) to form the enzyme substrate complex (ES). The enzyme–substrate complex then reacts to the product molecule (P) and regenerates the active site of the enzyme (E) in what is considered to be the rate-limiting step of the proposed scheme:

k2

E + S ES E + P

→

k1 k3

Langmuir chemo kinetics should be equivelent to Michaelis–Menten kinetics since the total number of sites (the number of enzyme molecules) or the number of reaction sites on a surface is a constant. In addition, the often physically unrealistic assumption is made that k1, k2andk3 are independent of concentration.

The Michaelis–Menten rate expression as written in biochemistry is

(reactant) concentration. One can rewrite V in terms of an expression which is analogous

Molecular Heterogeneous Catalysis. Rutger Anthony van Santen and Matthew Neurock

Copyright © 2006 WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim

ISBN: 3-527-29662-X

314 Chapter 7

to the site normalized rate expression used conventionally in chemocatalysis by dividing V by the total number of enzyme sites [ET]:

where kr is the elementary rate constant of the rate-limiting reaction step is to be identified with k3. The inverse of the Michaelis–Menten constant KM −1 is the equivalent of the Henry coe cient or adsorption constant. θM.M is the fraction of enzyme molecules occupied by substrate:

[ES] θM.M = ET

When θM.M 1, the turnover number (or turnover frequency) of the reaction is deter-

=

mined by kr. The turnover frequency determined by k3 for most enzymes varies between 1 and 104 sec−1 . The highest value is found for the carbonic anhydrase enzyme, which will be discussed in Section 7.4: k3 = 6 x 105sec−1. It is interesting to compare this value for kr with that measured for a fast heterogeneous reaction such as hexene isomerization over protonic zeolites, which has a corresponding kr of only 10−2 sec−1. The rates found in zeolite catalysis thus tend to be much lower than those in enzyme catalysis. This is due to the much higher activation energies required for the protonation reaction in a zeolite as compared with analogous reaction(s) carried out by the enzyme. This can be understood by referring to Chapter 4, page 203. We illustrated for chymotrypsin how well-positioned acid and base functional groups in the enzyme cavity were responsible for its high rate of reaction. There is an optimum match between several peptide reactive groups and the geometric structures of the transition state.

A unique feature of the enzymes is their hydrophobic interior and hydrophilic exterior character. Their hydrophilic external surface makes them water-soluble. Their hydrophobic interior and unique internal electrostatic properties permits reactivity not possible in an aqueous medium alone. It also provides for selectivity advantages since the adsorption of apolar molecules tends to be preferred over that of highly polar molecules. For example, the subsequent reactions that arise in oxidation catalysis from the readsorption of the polar product molecules formed via the oxidation of an apolar reactant are suppressed in the hydrophobic cavity of the enzyme. This significantly enhances the enzyme’s overall selectivity.

Biocatalytic systems are part of biochemical systems that uniquely couple mass and energy transport. Enzymes are part of complex biochemical process systems. For instance, electron transport and proton transport drive catalytic systems electrochemically so that chemical potentials can be established for reactions to occur under mild conditions. Reduction processes, for example, can occur directly by electrochemically generating reducing agents such as NADH (nicotinamide adenine nucleotide, reduced form) or NADPH (nicotinamide adenine dinucleotide phosphate, reduced form). While it is outside the scope of this book to discuss these reactions in detail[1], some of the biocatalytic aspects will be discussed in later sections. A specific system that combines multiple reaction centers with rotational motion is the catalytic system adenosine triphosphate synthase, which we will introduce in Section 7.3. In this system, the chemical potential gradient that develops over the membrane acts control to proton transport. It can accept or generate the free energy of the chemical reaction.

Mechanisms in Biocatalysis; Relationship with Chemocatalysis 315

Biochemical systems are also often reaction cycles where the key catalytic intermediate is generated, consumed, and subsequently regenerated as the part of the complex reaction cycle. Enzymes catalyze the formation of the intermediates that participate in the overall reaction cycle. These are intricately catalyzed reaction systems where the intermediates that form subsequently act as catalysts. The citric acid cycle, which was discussed in Section 2.1 (see also Fig. 2.5), is one such cycle. Two other complex reaction systems comprised of many catalytic steps that are of key metabolic importance are the Calvin and glycolytic cycles.

In the Calvin cycle, CO2 is converted into hexose or fructose. 3-Phosphoglycerate is the key catalytic molecule that is consumed and generated in this cycle. In the citric acid cycle, citrate is the intermediate species in the sequence of oxidation steps that lead to

CO2.

In the glycolytic cycle, energy is regenerated by converting glucose to pyruvate. In the overall reaction, energy is produced and stored by the conversion of two molecules of ADP (adenosine diphosphate) to two molecules of ATP. Energy production and mass conversion are coupled. The autocatalyic system then involves self-organizing features together with kinetics that display oscillatory behavior. We will discuss this in more detail in Chapter 8. Autocatalytic reactions, which are part of the above-mentioned biochemical cycles, are essential to produce such self-organizing reaction systems.

A unique autocatalytic reaction mechanism can occur in biochemical systems due to enzyme modification as a consequence of pH changes during the catalytic cycle. Enzyme activity can be accelerated or inhibited by such pH changes, and in addition, by the enzyme interaction with specific molecules. An example of such an enzyme is ATP-synthase discussed in Section 7.3. The allosteric enzymes are a second class of enzymes that display unique reaction mechanisms in that they do not obey classical Michaelis–Menten kinetics. Allosteric enzymes are enzymes that contain several binding sites. Binding at one site a ects binding at another site, for instance by conformational changes in the protein. In chemocatalysis this would lead to non-Langmuirian adsorption behavior. In enzymes this can lead to increased as well as decreased binding of reactant molecules. When molecules produced in a reaction provide for positive feedback through activation of such allosteric enzymes, the system is autocatalytic.

7.2 The Mechanism of Enzyme Action; the Induced Fit Model

Enzymes are comprised of proteins which have definitive primary structures that can organize into secondary, tertiary and even quaternary structures. The enzyme consists of a peptide framework that contains cavities in which the catalytically reactive centers are incorporated. The enzyme protein is typically about 20–40 nm in size. The catalytically reactive centers can be part of the peptide that builds the enzyme framework such as carboxylic acid groups, or consist of cationic centers such as the porphyrins or nonreducible cations as Zn2+ or Mg2+ directly attached to the protein cavity. As mentioned earlier, the external part of the enzyme is hydrophilic and the internal microcavity is hydrophobic, with the possible exception of the often polar reaction center. In enzymatic reactions, the match between shape and size of reactant or product and catalytic center cavity is important.

Upon reaction with a substrate molecule, the shape of the enzyme is altered. The flexibility of the peptide framework implies that changes in overall protein shape (induced, for instance, by allosteric e ects) may a ect the shape of the reaction center. This will