
Molecular Heterogeneous Catalysis, Wiley (2006), 352729662X
.pdf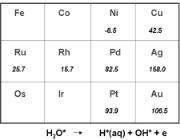
276 Chapter 6
Figure 6.9. Periodic trends in the reaction energy for the protolysis of water to form surface-adsorbed hydroxyl intermediates and hydronium ions in solution.
reported in Fig. 6.9.
In addition to its influence on stabilizing charged states, water can also directly participate in elementary physicochemical processes such as reaction and di usion. We have already described the fact that water can be directly involved in a chemical reaction by providing a conduit for proton transfer. Similarly water can aid in the di usion of charged surface intermediates. For example, Vassilev et al.[6] found that adsorbed OH intermediates demonstrated enhanced mobility on the Rh(111) surface when additional water molecules were coadsorbed. The increased di usion was the result of fast proton transfer through neighboring water molecules and the adsorbed OH. Protons transfer in the opposite direction, thus giving the impression OH migration in the forward direction (see Fig. 6.10). This is a Grotthus-like mechanism which has been used to describe hydroxyl mobility in H2O[12] . Desai and Neurock[3b] found similar results for the activation of water in an aqueous solution adsorbed on a PtRu surface. Their ab initio molecular dynamics results show that the OH hopping is quite rapid, occurring in only a few picoseconds. The barrier for proton transfer was found to be very low.
6.2.3 Influence of Potential
The results for the dissociation of water at the metal/solution interface show the wellknown double-layer structure that is at the heart of most electrochemical systems. While the negative charge is delocalized, it still acts to polarize the surface. The proton which forms exists as either a hydronium (H3O+ ) or a Zundel (H5O2 + ) ion both of which are about one solvation shell removed from the surface. This is known as the inner-layer Helmholtz layer. The chemistry that occurs at the interface polarizes the surface, which ultimately leads to a potential across the interface. In an actual system, the electrolyte plays an important role in establishing the potential as well as in potentially altering the structure and chemistry that occur at the interface.
Modeling electrochemical systems from first principles presents a considerable challenge. Quantum mechanical simulations are typically carried out within the canonical ensemble formalism where the number of electrons remains constant. The free energy is calculated with a constant temperature, volume and number of electrons F (T, V, N e). Electrochemical systems, on the other-hand, are typically performed at a constant chemical potential in the grand canonical ensemble where µ(T, V, N e) is a constant. Throughout this book we have presented examples where the number of electrons is preserved upon chemical reaction. In order to model an electrochemical system, we would have to model
Mechanisms for Aqueous Phase Heterogeneous Catalysis and Electrocatalysis 277
the structure and chemistry that occur at the anode simultaneously with that which occurs at the cathode, the rate of electron transfer through the circuit that connects the two, along with the rate of ion transport across the cell and local changes in electrolyte composition. This is not currently possible.
Various approximate approaches, however, have been taken in order to simulate electrochemistry at an electrode surface. Some of the first quantum mechanical models were developed by Anderson[13] , who used non-charge self-consistent atom superposition and electron delocalization (ASED) molecular orbital theory to probe changes in the polariza-
tion and hybridization and their influence on surface bonding. Bagus and Pacchioni[14], Illas and Mele[15] , Lambert[16] , Curulla and Clotet[17], Head-Gordon and Tully[18] and
more recently Wasileski et al. [19] demonstrated both qualitatively and quantitatively the influence of electrode potential on the intramolecular bond stretching known as the Stark e ect.
There have been very few ab initio e orts, however, aimed at examining the influence of an applied potential on electrochemical reactions. Anderson and co-workers have developed models to determine the reversible potentials for reactions occurring at the outer-sphere as well as within the double layer, and the activation barriers for electron transfer reactions.[20],
Anderson and co-workers calculated reversible potentials for outer-sphere processes by
using the following equation for the Gibbs free energy: |
|
∆Go = −nF U o |
(6.2) |
where n is the number of electrons that transfer and F the Faraday constant. They derived the following semiempirical expression in order to estimate the internal energy:
U 0 = (Er eV −1 + c)V |
(6.3) |
which linearly relates the reaction energy Er to the internal energy. The reaction energy can be calculated using ab initio methods quite easily. The term c, in Eq. (6.3) refers to an empirical parameter which can capture some of the features of the local environment and, hence allow for such a linear trend. The value of c for reactions involving O2 reduction in acid is 0.49 for MP2-type calculations and also B3LYP using 6–31G**. The constant will change based on the system which is being analyzed. This approach is typically limited to outer-sphere reactions run in acidic media.
The second method extends these ideas and is able to calculate reversible potentials for reactions that occur within the double layer. The model can be used to simulate both oxidation and reduction within the double layer. The influence of counterions from the electrolyte on the reactions can also be included. This is accomplished by using point charges and a Madelung sum in order to calculate the longer range electrostatic interactions and the field that arises from these ions and their influence on the reaction center.
The reversible potential models are limited to overall reaction energies. The activation barriers for electron transfer at electrode surfaces were modeled by establishing a reaction center and following the radiationless electron transfer into or out of an open system. The reaction center refers to the specific structural system where oxidation or reduction occur. The system is open, thus allowing electrons to transfer in and out. Electron transfer in the system occurs without an activation barrier when the electron a nities (reduction)
278 Chapter 6
or ionization potentials (oxidation) directly match the thermodynamic work function of the electrode (U = 0). For the standard hydrogen electrode this can be written as:
EA = eU + 4.6 eV |
(for reduction) |
(6.4) |
IP = eU + 4.6 eV |
(for oxidation) |
(6.5) |
In order to calculate the activation barrier for a specific potential, one has to establish the structure and corresponding energy of the reaction complex for constant electron a nity (EA) or ionization potential (IP ) surfaces. The minimum energy point on the corresponding surface is then the activation barrier.
The method was first used to treat outer Helmholtz plane reactions such as
Pt−OH2 . . . OH2(OH2)2 ←→ Pt−OH2 . . . H+−OH(OH2 )2 + e−(U ) |
(6.6) |
The activation energies can be calculated as the internal energy required for electron transfer to occur and are therefore activation internal energies rather than the activation free energies described by Marcus[21] .
The approach was used to study the electrochemical dissociation of H2O at an anode
at electrode potentials of 0.6 V (NHE) on Pt. The reaction sequence used is |
|
||||||
H |
O |
−→ |
OH |
ads |
+ H+ |
+ e−(U ) |
(6.7) |
2 |
|
|
solv |
|
|
||
where U is the electrode potential.
The solvation structure of the proton was taken into account by modeling it as a solvated hydronium ion H3O+ (H2O)2. Ab initio SCF-HF MP2 theory was used along with small Pt atom clusters to show that the dissociative adsorption of H2O requires the
direct assistance of additional H2O molecules: |
|
Pt−HOH . . . OH2(OH2)2 −→ PtOH . . . H+ · OH2(OH2) + e−(U ) |
(6.8) |
The approach was later extended to include explicit solvent molecules and Madelung potentials in order to begin to model the influence of solution and electrolyte. The approach begins to capture features of the elementary electrochemistry but does not include the e ects due to electrode potential on bond polarization or more complex reaction environments.
Halley and Mazzolo[22] developed a first-principles-based direct dynamics method to examine the water/copper metal interface. Previous models on the electrochemical metal/ water interface published in the literature could not straightforwardly describe the asymmetry of the capacitance measured experimentally in the double layer. In approach taken by Halley and Mazollo, the electrons in the metal are modeled quantum mechanically using a jellium-type free electron model where only the s-electrons in copper are treated. Pseudopotentials are used to describe the electron interactions with water. The water solution phase is decoupled from the electronic structure and treated by molecular dynamics simulations with explicit water molecules using classical force fields. Gouy–Chapman theory is used to treat ionic screening. The electronic structure at the interface between the metal and the water is carefully matched by performing electronic structure calculations on the metal substrate after each time step in the water MD simulation. The approach was used to examine the influence of applied potential on the structure of the metal-water

Mechanisms for Aqueous Phase Heterogeneous Catalysis and Electrocatalysis 279
interface. The system size examined was very large, including a solution layer comprised of 245 water molecules sandwiched between two metal layer slabs, each of which contains 36 metal atoms per layer. The simulations explicitly account for electronic structure contributions and on the influence of the double layer observed interfacial structure. The results show that more strongly bound water can lead to metastable charging at the interface. Water molecules that sit at atop sites tend to be very sensitive to potential and may help to explain previous X-ray structural data for water adsorbed on Cu and the asymmetry in the capacitance. The results also suggest that the macroscopic field is e ectively screened to a significant degree near the interface.
Nørskov et al.[67] recently developed a simple approach to examine electrocatalytic reduction of oxygen over Pt. More specifically, they examined the reaction sequence pro-
posed in Eqs. (6.9–6.11) as a model of the chemistry at the cathode. |
|
||
1 |
O2(g) + −→ O |
(6.9) |
|
|
|
||
|
2 |
||
O +H+ + e −→ HO |
(6.10) |
||
HO +H+ + e −→ H2O + |
(6.11) |
||
In their approach, they set a reference potential equal to that of the standard hydrogen electrode:
21 H2(g) −→ H+ + e−
. This can then be used to relate electrocatalytic reactions proposed in Eqs. (6.9–6.11) to the simple surface reaction energies defined in Eqs. (6.12–6.13).
H2O + −→ HO +1/2H2(g) |
(6.12) |
H2O + −→ O +H2 (g) |
(6.13) |
by separating out the electron transfer terms. The free energies for the electrocatalytic reactions (6.10) and (6.11) can be equated with the reverse reaction energies of Eqs. (6.12) and (6.13) at the electrode potential U = 0 by taking their relative energies with respect to the standard hydrogen electrode
H+ + e −→ 12 H2(g)
The energies for the individual surface intermediates are simply shifted by the electrode potential, –eU . They explicitly examine the influence of surface water molecules and the e ects of coverage in their calculations of the intermediate binding energies. The solution pH is accounted for by calculating the value of the free energy with respect to the system pH by the following classical expression:
G(pH) = −kT ln[H+] |
(6.14) |
The gas-phase surface energy calculations were then used to calculate the influence of electrode potential on the O2 reduction scheme presented above. They then used this
280 Chapter 6
methodology to examine a range of di erent transition metal surfaces in order to map out periodic trends and establish metals that would be most e ective. In addition to the mechanism proposed in Eqs. (6.9–6.11), they also examined a mechanism in which the O2 bond remains intact before the addition of hydrogen.
More recently, Lozovio et al.[23] developed a first-principles periodic DFT supercell approach for simulating the metal vapor phase interface at constant chemical potential. In this approach, charge is either added to or removed from the metal in order to fix an applied electrochemical potential. Charge neutrality within the supercell is maintained by adding an opposite background charge into the vacuum region. The background charge is added to a reference plane which lies parallel to the surface at some distance into the vacuum region. For simplicity, this can be chosen to be the center of the vacuum region. The electrostatic potential along this plane is then defined as zero. Placing the charge sheet at a fixed distance into the background has two important e ects. It acts as a reference electrode and it terminates the field at some finite distance from the surface. In addition, it defines the energy zero by which to reference di erent systems. The chemical potential is then defined as the energy to move an electron from the metal to this fixed reference electrode or take an electron from the reference electrode and place it within the metal.
The approach requires that both the energy and the potential be corrected for carrying out such a process. The correction to the DFT-calculated energy is
Ees = EesDFT + |
q |
V DFT Ω0 |
+ |
πq2 |
− |
Lz |
|
(6.15) |
A0 |
A02 |
3 |
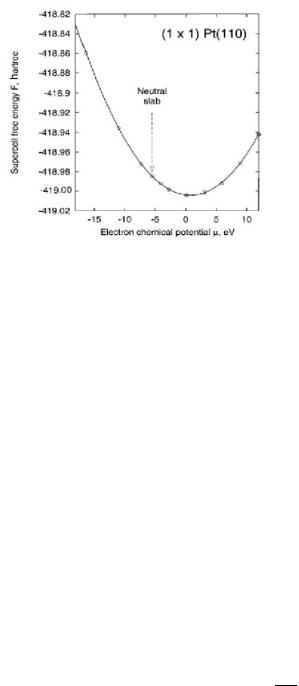
where EDFT and V DFT refer to the uncorrected electrostatic energy and potential, respectively, that are the direct result from the periodic DFT calculations, V DFT Ω0 is the average electrostatic potential which can be calculated by integrating the potential derived from the electronic structure calculations over space, q is the net charge that is added or removed from the system, A0 is the cross-sectional area of the unit cell in the z = 0 plane, Lz is the total length of the cell in the z direction, L is the distance from the surface (z = 0) to the background reference electrode, Ω0 refers to the volume of the cell and is the distance from the surface into the double layer. To test the system for Pt, the Helmholtz free energy was plotted with respect to the chemical potential. The results which are shown in Fig. 6.10 indicate a parabolic behavior whereby the minimum free energy lies close to µ = 0, as should be expected. The approach has more recently been used to examine the stability and possibility of reconstruction of Pt(110) and Au(110) surfaces under di erent electrochemical conditions [23].
Filhol and Neurock[24] established a similar constant charge (canonical) approach in order to simulate electrochemistry at aqueous/metal interfaces. A potential across the interface is induced by tuning the charge in the metal. This change in charge of the metal is compensated for by the addition of an equal, but opposite, change in charge, distributed homogeneously over the background of the cell. The homogeneous background used in these simulations is similar to that defined by others for other solid-state systems[23,25]. The addition (or removal) of charge at the surface of the metal subsequently polarizes the homogeneous background charge density in the solution layer and thus orients the water molecules at the water/metal interface. Heterolytic reactions subsequently go on to form the well-known double-layer structure at the interface.
The approach subsequently uses a double-reference system in order to determine the potential. By comparing the energies for di erent structures at a given potential, one
Mechanisms for Aqueous Phase Heterogeneous Catalysis and Electrocatalysis 281
Figure 6.10. Ab initio calculations of the Helmholtz free energy with respect to the chemical potential
[23].
is able to determine the free energy di erence between these given states at a constant potential, thus allowing for constant chemical potential calculations. The approach has been used to examine various electrochemical reactions at the metal/solution interface.
In the Filhol–Neurock approach, the total energy (EDFT) of the charged slab with ne electrons and a background charge of nbg is described by the following expression:
EDFT(ne, nbg ) = Eslab(ne) + Eslab−bg (ne, nbg) + Ebg (nbg ) |
(6.16) |
where Eslab is the energy of the slab without a background, Ebg is the energy of the background without a slab and Eslab−bg the interaction energy between the slab and the background.
The charge which is delocalized over the surface of the slab and the compensating background charge interact with one another and therefore must be corrected for in order to determine the true total energy. The values for ne and nbg are not independent as mne = −nbg = q. The general relationship between the chemical potential µ and the total energy (E) therefore does not hold true for the total energy of the unit cell:
µ = |
∂ne |
|
= |
∂q |
− |
|
(6.17) |
|
∂E(ne , nbg) |
|
|
∂EDFT(q, |
|
q) |
|
nbg
The description of the total DFT energy, EDFT, must therefore be corrected for the interaction between the electrons in the slab and the background charge as was done in Eq. (6.16).
The slab and background are ultimately decoupled and the total electron energy can be defined as
q
Eelec = EDFT + Vtot(Q) dQ (6.18)
0
where

282 Chapter 6
V (q) = |
unit cell |
|
V (→r )d →r |
(6.19) |
|
|
|
1 |
|
|
|
This satisfies the relationship given in Eq. (6.11). The total free energy of the system (EFree ), which includes contributions for the excess electrons (q) at the Fermi potential φvac and is equivalent to
q
EFree = EDFT + Vtot(Q) dQ − qφvac (6.20) 0
The potential-dependent energies presented here refer to the EFree values.
The chemical potential, φvac, referred to as the vacuum level is obtained directly from the calculations by using the Janak[26] theorem. The corresponding potential, U , which is referred to the standars hydrogen electrode, is extrapolated from the chemical potential
according to the experimental relationship [27]: |
|
|||
U |
= −4.85 − |
φ |
(6.21) |
|
|
|
|||
e |
||||
in order to allow for the direct comparison with the experiments. The value of U for the standard hydrogen electrode was calculated by Taylor et al.[32] to be 4.51 at 0 K and 4.67
at 300 K, which are in very good agreement with experimental values.
To simulate constant potential systems, one maps out the free energies between di erent states of the system over a range of di erent potentials. The free energy between states can then be calculated at any fixed potential. This approach has been used to examine the structure and reactivity of the aqueous water/metal interface under electrochemical conditions. Some of the results are summarized in the next section.
6.2.4 Electrochemical Activation of Water
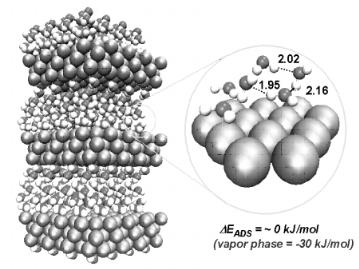
We start our discussion with the adsorption and activation of water over Pd(111) and then advance to other metals. Filhol and Neurock[24] used the approach described above to examine the potential–dependent behavior of water over Pd(111). In the absence of an electrochemical field or potential, water adsorbs on Pd(111) with its oxygen end directed down towards the surface and its molecular plane tilted away from the surface normal vector by approximately 60◦, as shown in Fig. 6.11.
Figure 6.12. The structure of the adsorbed water in an aqueous medium as a function of electrode potential. The snapshots follow the well-known water flip-flop mechanism as one moves from a potential
of zero charge to more cathodic potentials. The dark atoms refer to oxygen and the light atoms refer to hydrogen[24].
Mechanisms for Aqueous Phase Heterogeneous Catalysis and Electrocatalysis 283
Figure 6.11. The adsorption of liquid water on Pd(111). The binding energy for water on Pd(111) in the vapor phase is 30 kJ/mol. The binding energy for liquid water is –2.5 kJ/mol[3b]. The dark atoms refer to oxygen and the light atoms refer to hydrogen.
This is consistent with the results described earlier for the single bilayer structure of water on di erent transition-metal surfaces. As the potential is decreased to more negative values, water flips over, whereby its hydrogen atoms are now directed toward the surface. This is seen in the sequence of structures for decreasing potential in Fig. 6.12. This change in the water structure is well known in electrochemistry as the “water flip-flop” mechanism [28]. Further decreases in the potential result in the stretching of the O–H bond. The O–H bond ultimately breaks to form an OH− intermediate along with a surface hydride. The hydroxyl ion readily migrates into solution. A further decrease in the potential drives the OH− species further away from the metal surface. This is the result of field-induced electromigration (di usion). The phase transition for the activation of water to form the surface hydride appears to occur at 550 mV. This is consistent with electroadsorption of hydrogen experiments over Pd(111) which indicate that the reaction
(Pd−H2 O) −→ (Pd−OH) + H+ + e− |
(6.22) |
proceeds at 0.4 V with respect to the hydrogen electrode[29] .
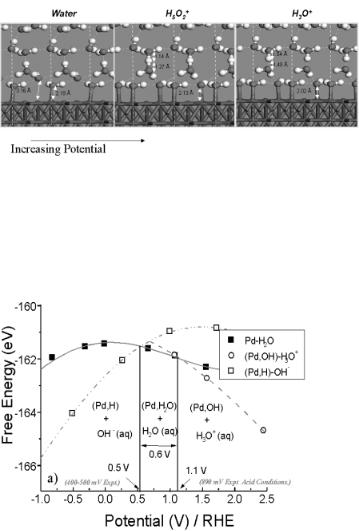
At potentials which are slightly greater than the potential of zero charge, water is adsorbed with its oxygen end pointed down towards the surface. Upon further increase in the potential, water reacts to form a surface hydroxide intermediate along with a proton, which migrates into the aqueous phase to form either a hydronium or a Zundel ion, as showns in Fig. 6.13. The phase change for the conversion of water to hydroxide on Pd(111) appears to occur at 1100 mV (pH = 7). The experimental results for this system indicate that water reacts to form adsorbed hydroxide and protons at 0.8 V. The experimental results, however, were obtained in an acidic medium. Correcting for pH could shift the calculated potential closer to the actual experimental potential of 800 mV[22,28]. The composition under electrochemical conditions, however, is ill-defined, thus making it di cult to compare theory and experiment directly.
284 Chapter 6
Figure 6.13. The anodic activation of water on Pd(111) to form adsorbed hydroxyl intermediates and hydronium ions. The dark atoms refer to oxygen and the light atoms refer to hydrogen[21].
The phase diagram for the activation of water to form surface hydride and surface hydroxide phases is shown in Fig. 6.14. The comparison of di erent structures at a given potential can be compared in order to determine the free energy di erences between these phases at a constant chemical potential.
Figure 6.14. Ab initio-calculated electrochemical phase diagram for the activation of water over Pd(111)
to form either the surface hydride phase along with aqueous OH− ions or a surface hydroxide phase along with hydronium ion[21].
Similar calculations were carried out for water activation over Cu(111), Ni(111) and Pt(111) surfaces[31] . The calculations for water on Cu(111) go into much more detail and show that the surface structure changes continuously as a function of applied potential [31,32]. The results show that various additional surface phases can form that were not explored over Pd(111). The snapshots outlined in Fig. 6.15 are the result of increasing the charge in the system from what would be negative potentials to positive potentials. In order to establish explicitly whether or not one of these phases exists would require mapping out a detailed phase diagram for all of the phases, which is currently in progress. Even without the entire phase diagram, the results presented in Fig. 6.15 are rather en-

Mechanisms for Aqueous Phase Heterogeneous Catalysis and Electrocatalysis 285
Figure 6.15. The structural changes of water and its reactivity on Cu(111) as a function of applied potential.[32].
lightening as they show the full range of di erent structures that can form. In moving from neutral potentials to more negative potentials, water flips over as was already discussed for water on Pd(111). At more negative potentials, water dissociates to form a surface hydride along with hydroxyl intermediates that move into solution. This occurs at –0.95 V for basic conditions. At more negative potentials, subsequent water molecules can dissociate to begin to form OHOH chains in solution along with the evolution H2.
As the potential is increased from the potential of zero charge, water becomes more oxidized and moves from the favored atop site to a bridge site. Further increases in the potential lead to the activation of an OH bond and the formation of a surface hydroxide which binds in a two-fold hollow site and proton which migrates into the solution to form a hydronium ion. On Cu(111), the potential for this to occur was calculated to be –0.5 V for basic conditions. At even higher potentials, the OH intermediate moves from the two-fold bridge site to the 3-fold fcc site. Further increases in the potential lead to the formation of a surface oxide layer and ultimately dissolution of the metal. At even higher potentials, place exchange between adsorbed atomic oxygen and surface metal atom can proceed, thus allowing for the dissolution of Cu. While the specific potential at which this occurs has yet to be determined, the results suggest that it is possible to begin to examine the reactivity of the aqueous/metal interface and the stability of such interfaces to changes in the potential.
The examples that follow below outline how we can begin to extend the general mechanistic information gleaned from gas-phase surface reactions to more complex liquid phase systems and electrochemical systems.
6.3 The Synthesis of Vinyl Acetate via the Acetoxylation of Ethylene
Vinyl acetate is synthesized via the selective oxidation of ethylene and acetic acid over supported Pd and PdAu catalysts via the reaction
CH2=CH2 + CH3COOH + |
1 |
|
+ H2O |
(6.23) |
2 O2 CH2=CHO(O)CCH3 |
||||
