Molecular Heterogeneous Catalysis, Wiley (2006), 352729662X

256 Chapter 5

5.7.2 The Sulfide Surface

The most widely studied sulfide surface is that of MoS2. A short review of the most salient features of the MoS2 surface is presented here. An important question that illustrates many aspects of the sulfide surface is that of the shape and morphology of the particles that form when the particles are dispersed on an inert support. Figure 5.22 shows that there are predominantly two di erent types of reactive surfaces present.

Figure 5.22. Atomic ball model (top view) showing a hypothetical, bulk-truncated MoS2 hexagon exposing the two types of low-index edges, the S edges and Mo edges. The Mo atoms (dark) at the Mo edge are coordinated to only four S atoms (light). To the left, the stripped Mo edge is shown in a side view together with two more stable configurations with S adsorbed in positions predicted from theory; the 50% covered (monomer) and a 100% covered Mo edge (dimer). To the right is shown a side view of the S edge with a full coordination of six sulfurs per Mo atom. Plotted on the MoS2 hexagons are

−

vectors with length corresponding to the edge free energies γMo for the (1010) Mo edge and γS edge. The envelope of tangent lines drawn at the end of each such vector constructs a hexagon if γS equals γMo . If γS > 2 × γMo the result is a triangle (outlined shape) terminated exclusively by the Mo edge, or vice versa for the S edge. Intermediate values result in clusters with a hexagonal symmetry[113].

MoS2 consists of layers in which Mo cations, with formal ionic charge +4, are sandwiched between layers of sulfur atoms. Each Mo atom is prismatically surrounded by six sulfur atoms, each of which has three Mo atoms as neighbors. The interaction between the MoS2 layers is controlled by the weak van der Waals interactions and, hence, the MoS2 particles are slabs terminated by the coordinatively saturated sulfur atoms (see the central part of Fig. 5.22). We examine here the (100) surface.

The sulfided (100) surface is unreactive. Two di erent reactive surfaces are formed if the MoS2 is cut perpendicular to the surface plane. The first surface from such a cut is terminated with Mo atoms (Mo edge), whereas the second surface is S terminated (S edge). These are polar surfaces, one contains excess positive charge (Mo edge), the other excess negative charge (S edge). At the Mo edge, the Pauling ion charge excess of Mo is e+ = + 43 with no negative charge excess on S. At the S edge, the S ion however has a

charge excess e −= – 23 .

In Section 5.2, we discussed the fact that such polar surfaces are unstable and tend to reconstruct. The MoS2 edges become stabilized in vacuum because charge transfer between Mo and S is reduced. The Mo atoms at the Mo edge reduce to a state close to Mo3+. The sulfur atoms at the S edge reduce to a state close to S−, a state as we will see which is highly reactive for hydrogen. Exposed to a mixture of H2S and H2, this surface becomes covered with SH− groups.

Catalysis by Oxides and Sulfides 257

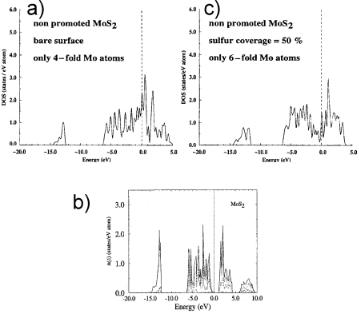
Figure 5.23. Local densities of states projected on the Mo sites (a) Mo edge 0% S, (b) bulk MoS2[24], the dark lines here refer to Mo DOS, (c) Mo edge 50% S[117b].

This reduction of MoS2 at the Mo edge follows immediately from a comparison of the electron density of states of bulk MoS2 (Fig. 5.23b) and that on the atoms at the edge (Fig. 5.23a). In the density of states (DOS) plot for bulk MoS2, we note a gap at the Fermi level (0.0 eV). The DOS below the Fermi level consists of electrons mainly localized on sulfur and the DOS above the Fermi level is located on Mo. The gap at the Fermi level implies that the system is an insulator with no conductivity. This is consistent with a description in which Mo has a formal charge of +4 and sulfur a formal charge of –2 Figure 5.23a shows a very di erent situation around the Fermi level; the highest occupied orbitals are now located at the MoS2 edge. The gap is no longer present, consistent with a conductive material implying that Mo is reduced. This reduction in charge is consistent with the reduction in the number of S neighbors from six to four, implying less electron donation from Mo atoms to sulfur atoms.

A similar conclusion is drawn when one considers the system to be completely ionic (a poor description) and computes the Madelung potentials at the Mo cation in bulk MoS2 compared with that on the surface. The decrease from six negatively charged neighbors to four implies a decrease in the relative stability of positive charge on the Mo atoms and, hence less of a driving force for electron donation from Mo to sulfur.

This reduction of charge is a general e ect that occurs on many reducible oxides or sulfides.

As illustrated in the center part of Fig. 5.22, the shape of the particle is triangular,

terminated with solely Mo or S edges, and is hexagonal when the surface energies of the two edges are similar. The morphology of the particle is determined by Wul [116]

258 Chapter 5

construction according to the law

γ(kke) = c d(kke)

The distance d of a surface with respect to the center of a crystal is proportional to its surface energy. Hence surfaces with large surface energies are only present at the crystal surface to a small extent. The planes with low surface energies tend to dominate.

Hence, when one of the surface energies changes (as expected in the presence of an H2S/H2 atmosphere), the particle shape will begin to deviate. At the reduced Mo edge, H2S will react and S atoms will attach as shown in Fig. 5.22 (left) (Mo edge at 50% S coverage).

Mo|−−| + H2S −→ MoS + H2

The S atoms adsorb between two edge Mo atoms. The reaction energy for H2S decomposition at the Mo edge remains exothermic up to the point where the S coverage reaches 50%. Each Mo center is once again six-fold coordinated to Mo and has a formal 4+ charge [see Fig. 5.22(left)]. The electron energy gap shown in Fig. 5.13b reappears at the Fermi level.

An extensive set of calculations have been carried out to produce the phase diagrams shown in Fig. 5.24 for the Mo and S edges as a function of H2S and H2 pressure, expressed as relative chemical potentials[24].

Figure 5.24. Phase diagrams for (A) the Mo edge and (B) the S edge with regions indicating the stable configurations for realistic values of ∆µS and ∆µH . The chemical potentials have been normalized with respect to the energy of bulk sulfur and half the energy of a single, isolated H2 molecule. Typical HDS conditions are indicated in the figures[113].

The chemical potential of hydrogen is defined with respect to PH2. ∆µH < −0.6 eV implies that no hydrogen is present. The chemical potential of H2S is determined with respect to the chemical potential of S in MoS2. ∆µS = 0 implies a high H2S partial pressure.

We note from the phase diagram that in the presence of hydrogen, the S edge remains 100% saturated over a wide hydrogen pressure interval, but is covered with SH groups. The Mo edge (50%) is more di cult to hydrogenate. At a maximum, half of the S atoms added to this edge then contain SH groups. Because the surface energies of these edges are di erent, the shape of the particle di ers from the ideal hexagon, see Fig. 5.25.

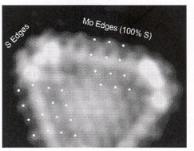
The conclusion from these studies is that under practical sulfide catalysis conditions, both the Mo edge and the S edge contain coordinatively saturated Mo atoms. The bright rim of white spots in the STM picture (Fig. 5.25) near the sulfide particle edge is indicative

Catalysis by Oxides and Sulfides 259

Figure 5.25. An atom-resolved STM image of a typical single-layer MoS2 hexagon exposed to H2S gas at 573 K. The white dots indicate the registry at the longer (Mo) edges. The registry of edge protrusions

and the bright rim reveals that the Mo edges have become resulfided to the fully saturated S2 dimer configuration[113].

of a high electron density at the Fermi level on the Mo atoms at the edge. The Mo atoms are partially reduced. Lauritsen et al.[118] have shown that the electronic state at these

Mo-edge atoms is metallic, forming a one-dimensional chain. In contrast to the interaction with bulk Mo atoms in the basal plane, thiophene interacts weakly with rim Mo atoms, notwithstanding these full coordinative saturation with S atoms. Below 200 K thiophene adsorbs in a flat five-coordinate η5 adsorption geometry through its π-electrons parallel to the plane of Mo atoms. When hydrogen is coadsorbed to the edge S-atoms, exposure of thiophene at 500 K leads to partial hydrogenation of thiophene and cleavage of a C–S bond. Theoretical calculations are in agreement with STM data and show that cis-but-2- enethiolate is formed. The hydrogen molecule will not dissociate under these conditions at the rim sites. In the experiment, hydrogen atoms had to be produced by dissociating hydrogen on a glowing tungsten filament.

5.7.3 Promoted Sulfide Catalysts

On an atomic level, the mechanistic basis to the promoting action of divalent reducible cations such as Co2+ or Ni2+ can best be illustrated by discussing in detail the H2/D2 exchange reaction on promoted and non-promoted sulfide systems[118] . Reactivity aspects of the terminated MoS2 surface have been investigated by several research groups[117−119]. We will limit our discussion to the Co2+/MoS2 system.

The Mo edge (50%) and the Co/Mo edge in which part of the center Mo atoms have been substituted by Co are shown in Fig. 5.26. Both edges are in equilibrium with a mixture of H2S and H2 of the same partial pressure. Whereas the non-promoted Mo edge (50%) contains only coordinatively saturated Mo, one notes that under the same condition the Co ions have a maximum coordination of five S atoms. This implies that a Co ion and a neighboring Mo cation remain coordinatively unsaturated. This can be readily understood once one realizes that Co2+ substitution of Mo4+ is not a charge-neutral substitution.

A charge-neutral substitution occurs when an [Mo4+S2−]2+ unit substitutes for Co2+ at the Mo edge, then Co2+ becomes directly accessible to S. Its dominant surface state has a coordination number of 5, in line with the expectation based on the charge neutrality argument. The activation of H2 on a coordinatively unsaturated edge of Mo or Co is energetically very di erent. Figure 5.26 illustrates adsorption modes for dissociatively adsorbed H2. Adsorption is heterolytic. One hydrogen atom adsorbs on the cation and the other on S. The reactivity of the S atom depends strongly on whether it is adsorbed

260 Chapter 5

Figure 5.26. Hydrogen adsorption on metal–sulfur pairs. Adapted from A. Travert et al.[119].

between two surface atoms, between two Co atoms or between an Mo and a Co atom. Adsorption is exothermic to Co and a S atom between two Co ions, or to a Co atom and an S atom between Mo and Co. Adsorption is endothermic to an Mo and an S atom between two Mo atoms. The calculation of activation barriers for the dissociative adsorption of H2 gives the following result:

The activation energy for H di usion is 30 kJ/mol. One notes that the activation energy for H2 dissociation on Mo is higher than the activation energy for recombination. On the Co site, this situation is reversed. On Co the rate of hydrogen atom recombination is rate limiting. Since the activation energy for di usion is low, these facts are consistent with the

experimental observation that on MoS2 the H2/D2 exchange reaction rate is first order in H2 or D2 pressure, whereas on Co/MoS2 it is only half order[120].

The increased reactivity of the CoS surface site stems mainly from the di erence in reactivity of an S atom coordinated between two Mo atoms as MoSMo compared with S between two Co atoms or Co and Mo. This is due to the weaker CoS bond energy which increases the SH bond of S bonded to Co instead of Mo.

Under conditions where desulfurization occurs at finite H2S/H2 ratio, the surface of MoS2 will be covered with S and not contain any vacancies, whereas on the promoted catalyst the presence of vacancies to adsorb a hydrocarbon will be present.

A comparison of the kinetics of a model desulfurization reaction:

thiophene + 2H2 −→ H2S + butadiene

catalyzed by di erent metals is shown in Fig. 5.27[121].

Kinetic data are given in Table 5.5. The catalysts are sulfide metal-containing particles dispersed on a carbon support. The rates are normalized on metal content. As can be

Catalysis by Oxides and Sulfides 261

Figure 5.27. Thiophene HDS activity for the di erent carbon-supported transition-metal sulfides under standard conditions (3.33 kPa thiophene, 1 kPa H2 S, and T = 573 K). Adapted from E.J.M. Hensen[121].

deduced from the orders for this reaction shown in Table 5.5, the coverage with reactive S increases in the sequence Mo, Ru, Rh, Pd and Ag. A high reaction order in H2S implies a low coverage with reactive sulfur and a low reaction order in H2S implies a high coverage with reactive sulfur. Thiophene and H2S compete for surface vacancies and, hence, between one another. In order to activate thiophene it has to adsorb with its sulfur atom on a metal surface atom. A high reaction order in thiophene implies that it does not easily compete with H2S adsorption or decomposition, and a low reaction order implies easy competition. One notes for the systems of maximum reactivity (the RhS system has a similar reactivity to the Co/MoS2 system) that the order of thiophene is a minimum, implying that for that system competition with H2S is optimum. This is consistent with earlier discussed equilibrium surface states of MoS2 and Co/MoS2.

Table 5.5. Reaction orders of thiophene (nT), H2 S (nS) and H2 (nH) under di erent conditionsa[121]

a 95% confidence interval for nT ±0.05, ns ±0.07, nH ±0.02. b Inlet H2S partial pressure: 0 kPa.

c Inlet H2S partial pressure: 1 kPa.

Whereas, the Mo (edge) does not contain vacancies, the Co-promoted system does and can therefore be covered to a high extent with reaction intermediates under the same reaction conditions.

262 Chapter 5

5.8 Summary

Quantum chemistry has reached the state where the reactivity of well-defined metal oxide and metal sulfide surfaces can be probed with reliable accuracy and chemical relevance. This becomes particularly clear in the first section of this chapter, where we analyzed the surface structures of acidic, covalent and ionic materials and their interaction with probe molecules. First-principle quantum mechanical results can readily be analyzed and understood in terms of semi-classical models. Semi-classical models such as the Pauling charge excess model provide an easy way in which to examine electrostatic e ects on surface acidity or basicity. The metal surface cations are analogous to those found in organometallic clusters. They can therefore be analyzed using essentially the same timehonored methods and theoretical frameworks that have been developed for organometallic systems with little modification. Isolable molecular orbital analyses were used herein to demonstrate how changes in the surface hybridization of atomic orbitals influence the general catalytic activity.

The semi-empirical models nicely demonstrate the di erences between various di erent oxide surfaces. Systems such as MgO in which di erences in the energies of adsorption sites are dominated by electrostatic potential di erences were explicitly distinguished from more covalent oxide systems such as alumina or silica surfaces. In addition, the models help to understand why surface reconstruction is often important when Lewis acid and base centers are converted into their corresponding Brønsted base and acid sites.

As was discussed more generally in Chapter 2, the influence of the reaction environment can significantly influence the intrinsic catalytic kinetics for both metal oxides and metal sulfides. Medium e ects were shown in this chapter to be extremely important in comparing gas-phase acidity with the acidity in solvents, and in addition, solid acidity with acidity in solution.

One of the greatest advances that theory has made over the past decade has been its ability to examine the sensitivity of the state of the working surface to changes in reaction conditions and surface structure. This has required the ability to integrate ab initioderived thermodynamic and kinetic results into phase equilibrium as well as atomistic kinetic simulations. The oxide and sulfide surfaces are su ciently stable that useful studies can be carried out. CO oxidation catalyzed by RuO2 demonstrated that the maximum turnover rate occurs under conditions where the surface is in a disordered state at the boundaries of two phases, one of which is completely covered with oxygen adatoms and a second which is partially covered with CO.

In a similar way, theory has been used not only to establish the nature of active sites on the surface but, in addition, to map out a full phase diagram for MoS2 as a function of the H2/H2S ratio. The results provided the ability to predict the state of the surface at specific conditions and to establish the region of phase space. This can ultimately be used in order to aid in the design of optimal operating conditions.

Mixed oxides and sulfides are very often used as catalysts to carry out a range of di erent reactions. On the sulfides it has become clear that the use of cations with di erent valencies creates surface vacancies not present on the non-promoted systems under the reaction conditions.

Catalysis by Oxides and Sulfides 263

References

1.H. Freund, Angew. Chem. Int. Ed. Engl. 36, 452 (1997)

2.L. Pauling, The Nature of the Chemical Bond, Oxford University Press, Oxford

(1950);

R.A. van Santen, Theoretical Heterogeneous Catalysis, World Scientific, Singapore (1991)

3.R. Refsin, R.A. Wogelius, D.G. Fraser, M.C. Payne, M.H. Lee, V. Milman, Phys. Rev. B, 52, 10823 (1995);

W.Langel, M. Parinello, J. Chem. Phys. 103, 3240 (1995)

4.M. Digne, P. Sautet, P. Raybaud, P. Euzen, H. Toulhoat, J. Catal. 211, 1 (2002)

5.A.A. Tsychanenko, V.N. Filimonov, J. Mol. Struct. 19, 579 (1972)

6.(a) C. Arrouvel, M. Digne, M. Breysse, H. Toulhoat, P. Raybaud, J. Catal. 222,

152 (2004);

(b) P.J.D. Lindan, N.M. Harrison, J.M. Holender, M.J. Gillan, Chem. Phys. Lett. 261, 246 (1991)

7.T.W. Dijkstra, R. Duchateau, R.A. van Santen, A. Meetsma, G.P.A. Gap,

J.Am. Chem. Soc. 124, 9856 (2002)

8.G.Pacchioni, Surf. Rev. Lett. 7, 277 (2000)

9.J. Sauer, P. Ugliengo, E. Garrone, V.R. Saunders, Chem. Rev. 94, 2096 (1994)

10.L.G.M. Petterson, M. Nyberg, J.L. Pascual, M.A. Nygren, in Chemisorption and Reactivity on Supported Clusters and Thin Films, R.M. Lambert and G. Pacchioni (eds.), NATO ASI Series E, Vol. 331 p. 425, Kluwer, Dordrecht (1997)

11.R. Wichtendahl, M. Rodriguez–Rodrigo, U. H¨artel, H. Kuhlenbeck, H.J. Freund, Surf. Sci. 423, 90 (1999)

12.G. Pacchioni, J.M. Ricart, F. Illas, J. Am. Chem. Soc. 116, 10152 (1994);

G.Pacchioni, A. Clotet, J.M. Ricart, Surf. Sci. 315, 337 (1994)

13.A.P. Seitsonen, Y.D. Kim M. Knapp, S. Wendt, H. Over, Phys. Rev. B, 65, 35413 (2001)

14.L. Zang, H. Kisch, Angew. Chem. Int. Ed. 112, 4075 (2000)

15.Y.D. Kim, S. Schwegmann, A.P. Seitsonen, H. Over, J. Phys. Chem. B, 105, 2205 (2001)

16.a) K. Reuter, M. Sche er, Phys. Rev. Lett. 90, 46103 (2003);

b) K. Reuter, D. Frenkel, M. Sche er, Phys. Rev. Lett. 93, 116105 (2004)

17.T.A. Albright, J.K. Burdett, M.H. Whangbo, Orbital Interactions in Chemistry, Wiley, New York, p. 404 (1985)

18.D.F. Shriver, P.W. Atkins, C.H. Langford, Inorganic Chemistry, Oxford, Oxford University Press, p. 248 (1994)

19.C.J. Ballhausen, Introduction to Ligand Field Theory, McGraw-Hill, New York (1962)

20.D.A. Dowden, D. Wells, Actes 2. Congress Int. Catalysis, Paris, p. 1499 (1961); D.A. Dowden, Endeavor, 24, 69 (1965)

21.V.B. Kazansky, Top. Catal., 11–12, 55 (2000)

22.D.A. Zhurko, M.V. Frash, V.B. Kazansky, Catal. Lett. 55, 7 (1998)

23.V.B. Kazansky, Catal. Rev. 43, 199 (2001)

24.T. Okuhara, N. Mizuno, Adv. Catal. 41. 113 (1996)

25.M.J. Janik, R.J. Davis, M. Neurock, J. Phys. Chem. B, 108, 12292 (2004)

264Chapter 5

26.M.J. Janik, K.A. Campbell, B.B. Bardin, R.J. Davis, M. Neurock, Appl. Catal. A, 256, 51 (2003)

27.B.B. Bardin, R.J. Davis, M. Neurock, J. Phys. Chem. B, 104, 3556 (2000)

28.M. Janik, R.J. Davis, M. Neurock, J. Catal. to be submitted

29.J.C. Vedrine, J.M.M. Millet, J.C. Volta, Catal. Today, 32, 115 (1996)

30.M. Che, Adv. Catal. 31, 78 (1982)

31.M. Che, A. Tench, Adv. Catal. 32, 1 (1983)

32.J. Haber, M.J. Witko, J. Catal. 216, 416 (2003)

33.D. Kulkarni, I. Wachs, Appl. Catal. 6162, 1 (2002)

34.M. Banares, Catal. Today, 51, 319 (1999)

35.M. Barteau, Chem. Rev. 96, 1413 (1996)

36.A. Corma, H. Garcia, Chem. Rev. 102, 3837 (2002)

37.J. Macht, C.D. Baertsch, M. MayLozano, S. L. Soled, Y. Wang, E. Iglesia,

J.Catal. 227, 479 (2004)

38.P.L. Gai, Top. Catal. 8, 97 (1999)

39.P.L. Gai, K. Kourtakis, Science, 267, 661 (1995)

40.K. Kourtakis, P.L. Gai, J. Mol. Catal. A Chem. 220, 93 (2004)

41.A. Andersson, S. Hansen, A. Wickman, Top. Catal. 15, 103 (2001)

42.G. Xiong, V. Sullivan, P.C. Stair, G.W. Zajac, S.S. Trail, J.A. Kaduk, J.T. Golab,

J.Brazdil, J. Catal. 230, 317 (2005)

43.H. Freund, Faraday Discus. 114, 1 (2000)

44.K. Reuter, C. Stampfl, M. Sche er, in Ab Initio Atomistic Thermodynamics and Statistical Mechanics of Surface Properties and Functions, S. Yip, (ed.) (2004) (to be published)

45.H. Hu, I.E. Wachs, J. Phys. Chem. 99, 10911 (1995)

46.Y. Chen, I.E. Wachs, J. Catal. 217, 468 (2003)

47.I.E. Wachs, Y. Chen, J.M. Jehng, L.E. Briand, T. Tanaka, Catal. Today 78, 13 (2003)

48.D.E. Fein, I.E. Wachs, J. Catal. 210, 241 (2002)

49.X. Wang, I.E. Wachs, Catal. Today, 96, 211 (2004)

50.L.J. Burchan, M. Badlani, I.E. Wachs, J. Catal. 203, 104 (2001)

51.V. E. Henrich, P.A. Cox, The Surface Science of Metal Oxides, Cambridge University Press, Cambridge (1994)

52.M. Barteau, Adv. Catal. 45, 262 (2000)

53.G.W. Coulston, E.A. Thompson, N. Herron, J. Catal. 163, 122 (1996)

54.G.W. Coulston, S.R. Bare, H. Kung, K. Birkeland, G.K. Bethke, R. Harlow, N. Herron, P.L. Lee, Science 275, 191 (1997)

55.J.C. Volta, C.R. Acad. Sci. Paris, Ser. IIC, Chimie 3, 717 (2000)

56.M. Havecker, A. Knop-Gericke, H. Bluhm, E. Kleimenov, R.W. Mayer, M. Fait, R. Schlogl, Appl. Surf. Sci. 230, 272 (2004)

57.J.K. Bartley, J.A. Lopez-Sanchez, G.J. Hutchings, Catal. Today, 81, 197 (2003)

58.K.E. Birkeland, S.M. Babitz, G.K. Bethke, H.H. Kung, G.W. Coulston, S.R. Bare,

J.Phys. Chem. B, 101, 6895 (1997)

59.V.V. Guliants, S.A. Holmes, J. Mol. Catal. A: Chem. 175, 227 (2001)

60.G. Centi, F. Cavani, F. Trifiro Selective Oxidation by Heterogeneous Catalysis,

Kluwer, New York (2001)

61.G. Centi, F. Trifiro, J.R. Ebner, V.M. Franchetti, Chem. Rev. 88, 55 (1988)

62.M. Neurock, G. Coulston, D.A. Dixon, unpublished work (1993

Catalysis by Oxides and Sulfides 265

63.E. Bordes, Acad. Sci. Ser. IIc: Chim. 3, 725 (2000)

64.G. Koyano, T. Saito, M. Misono, J. Mol. Catal. A, 155, 31 (2000)

65.A. Haras, H.A. Duarte, D.R. Salahub, M. Witko, Surf. Sci. 513, 367 (2002)

66.D.J. Thompson, M.O. Fanning, B.K. Hodnett, J. Mol. Catal. A: Chem. 198, 125 (2003)

67.M. Witko, R. Tokarz, J. Haber, K. Hermann, J. Mol. Catal. A: Chem. 166, 59 (2001)

68.D.J. Thompson, I.M. Ciobica, B.K. Hodnett, R.A. van Santen, M.O. Fanning, Surf. Sci. 547, 438 (2003)

69.D.J. Thompson, I.M. Ciobica, B.K. Hodnett, R.A. van Santen, M.O. Fanning, Catal. Today, 91–92, 177 (2004)

70.H. Liu, E. Iglesia, J. Catal. 223, 161 (2004)

71.J.M.M. Millet, J.C. Vedrine, G. Hecquet, Stud. Surf. Sci. Catal. 55, 883 (1990)

72.J.M.M. Millet, J.C. Vedrine, Appl. Catal. 76, 209 (1991)

73.J.M.M. Millet, D. Rouzies, J.C. Vedrine, Appl. Catal. A: General 124, 205 (1995)

74.C. Virely, M. Forissier, J.M.M. Millet, J.C Vedrine, J. Mol. Catal. 71, 199 (1992)

75.M.M. Gadgil, S.K. Kulshreshtha, J. Solid State Chem. 111, 357 (1994)

76.M.A. Chaar, D. Patel, M.C. Kung, H.H. Kung, J. Catal. 105, 483 (1987)

77.M.A. Chaar, D. Patel, H.H. Kung, J. Catal. 109, 463 (1988)

78.D.S. Sam, V. Soenen, J.C. Volta, J. Catal. 123, 417 (1990)

79.K. Chen, A.T. Bell, E. Iglesia, J. Phys. Chem. 104, 1292 (2000)

80.(a) I.E. Wachs, J. Phys. Chem. B, 109, 2275 (2005);

(b) J. Haber, in, R.A. Sheldon, R.A. van Santen (eds.), Catalytic Oxidation, World

Scientific, Singapore, p.40 (1995)

81.N.Y. Topsøe, M. Anstrom, J.A. Dumesic, Catal. Lett. 76, 11 (2001);

K.Hermann, M. Witko, R. Druzinic, R. Tokarz, Appl. Phys. A, 72, 429 (2001)

82.J.N. Allison, W.A. Goddard, in Solid State Chemistry and Catalysis, R.R. Grasselli,

J.Z. Brazdil (eds.), ACS Symposium Series, No. p. 279, 23. American Chemical

Society, Washington, DC (1985)

83.a) R.K. Grasselli, Top. Catal. 21, 79 (2002); b) J.C. Vedrine, Top. Catal. 21, 97 (2002)

84.M. Anstrom, N.Y. Topsøe, J.A. Dumesic, J. Catal. 213, 115 (2003)

85.K. Chen, A.T. Bell, E. Iglesia, J. Catal. 209, 35 (2002)

86.M.S. Palmer, M. Neurock, M.M. Olken, J. Am. Chem. Soc. 124, 8452 (2002)

87.L. Leveles, K. Seshan, J.A. Lercher, L. Le erts, J. Catal. 218, 307 (2003)

88.Y. Amenomiya, V. Birss, M. Goledzinowski, J. Galuszka,A. Sanger,

Catal. Rev. Sci. Eng. 32, 163 (1990)

89.J.H. Lunsford, Angew. Chem. Int. Ed. Engl. 34, 970 (1995)

90.M.Y. Sinev, V.N. Korchak, O.V. Krylov, Kinet. Katal. 27, 1274 (1986)

91.M.Y. Sinev, Catal. Today, 13, 561 (1992)

92.M.Y. Sinev, Catal. Today, 24, 389 (1995)

93.M.C. Wu, C.M. Truong, K. Coulter, D.W. Goodman, J. Catal. 140, 344 (1993)

94.M.C. Wu, C.M. Truong, K. Coulter, D.W. Goodman, J. Vac. Sci. Technol. 11, 2174 (1993)

95.D.J. Driscoll, W. Martir, J.X. Wang, J.H. Lunsford, J. Am. Chem. Soc. 107, 58 (1985)

96.L. Ackermann, J.D. Gale, C.R.A. Catlow, J. Phys. Chem. B, 101, 10028 (1997)

97.L.K. Dash, M.J. Gillan, Surf. Sci. 549, 217 (2004)