ИДЗ 19.2 вариант 1

1) Дана таблица распределения 100 заводов по производственным средствам Х (тыс. ден. ед.) и по суточной выработке У (т). Известно, что между Х и У существует линейная корреляционная зависимость. Требуется:

а) найти уравнение прямой регрессии у на х;

б) построить уравнение эмпирической линии регрессии и случайные точки выборки (Х;У).

Х	У								nх
	2,2	3,6	5,0	6,4	7,8	9,2	10,6	12
200	5	3	4	-	-	-	-	-	12
360	-	7	8	-	-	-	-	-	15
520	-	-	9	10	14	-	-	-	33
680	-	-	-	8	7	6	-	-	21
840	-	-	-	-	2	3	2	-	7
1000	-	-	-	-	-	-	6	6	12
nу	5	10	21	18	23	9	8	6	100

РЕШЕНИЕ

Составляем расчётную таблицу: (смотри файл «Таблица к заданию»).

Вычисляем выборочные средние и , , :

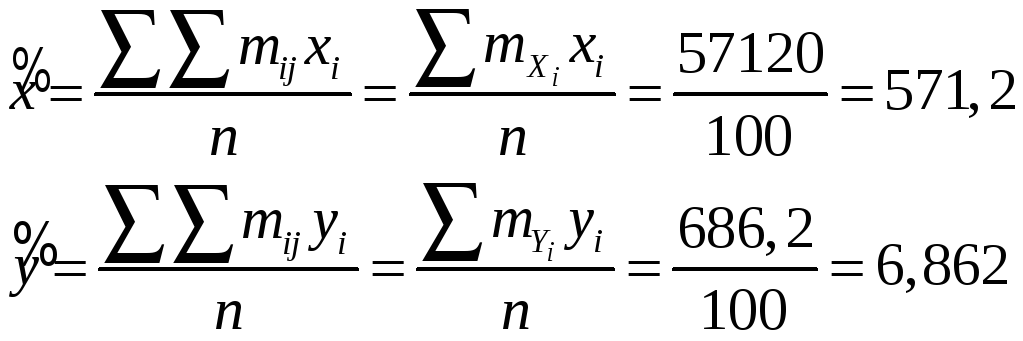
Найдём выборочные дисперсии:

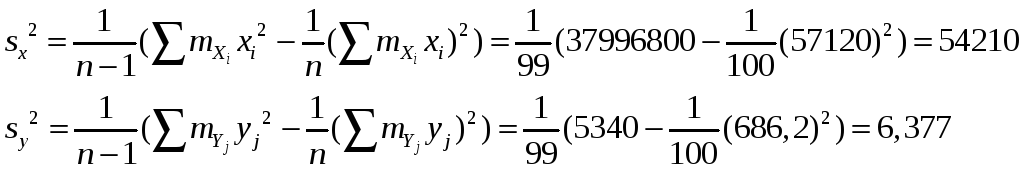
Найдём корреляционный момент:

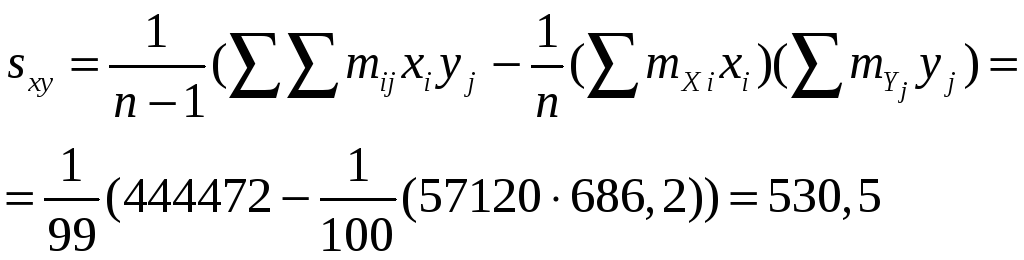
Оценка теоретической линии регрессии является эмпирическая линия регрессии, уравнение которой имеет вид:

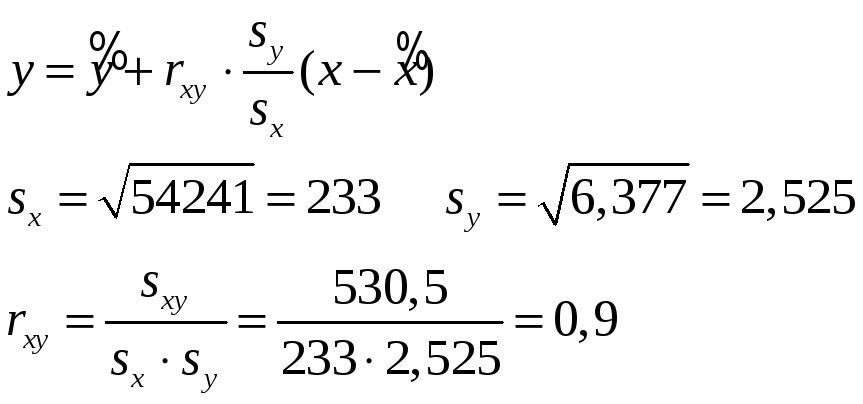
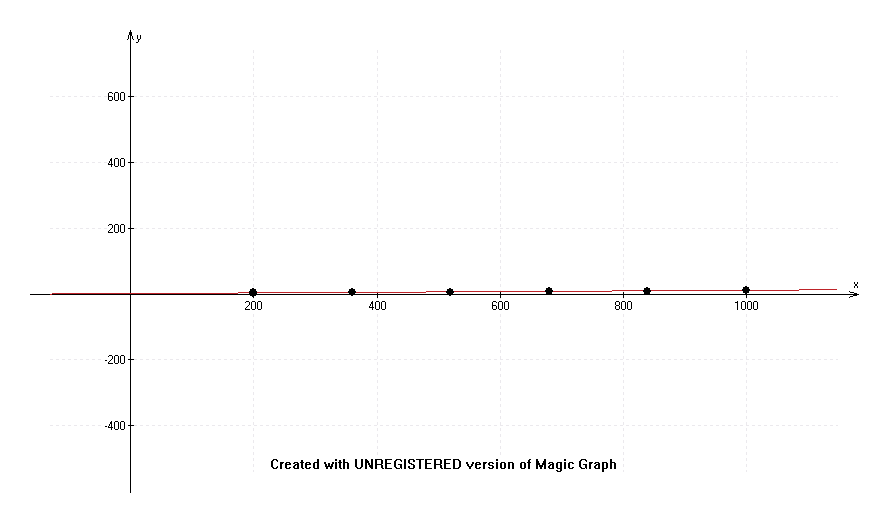
Составляем уравнение эмпирической линии регрессии у на х.

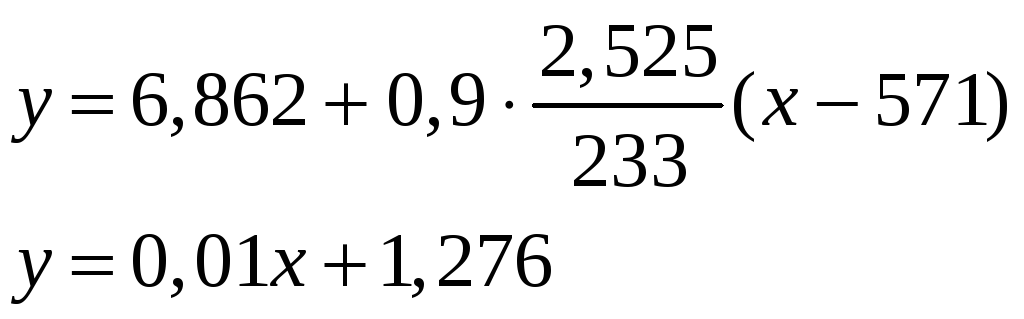
Строим линию регрессии и случайные точки .