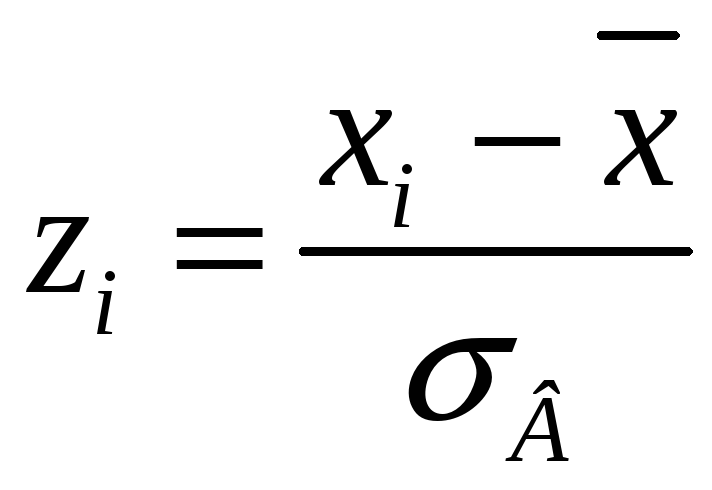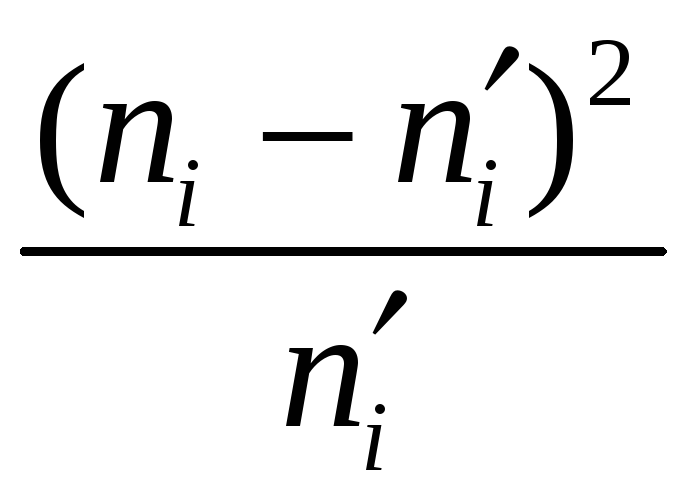ИДЗ 19.1 - 1
.1.doc1.1) В результате эксперимента получены данные, записанные в виде статистического ряда. Требуется:
а) записать значения результатов эксперимента в виде вариационного ряда;
б) найти размах варьирования и разбить его на 9 интервалов;
в) построить полигон частот, гистограмму относительных частот и график эмпирической функции распределения;
г) Найти числовые характеристики выборки
и
;
д) принять в качестве нулевой гипотезу
Н0: генеральная совокупность, из
которой извлечена выборка, имеет
нормальное распределение, проверить
её, пользуясь критерием Пирсона при
уровне значимости
;
е) найти доверительные интервалы для
математического ожидания и среднего
квадратичного отклонения при степени
надёжности
.
|
17,1 |
21,4 |
15,9 |
19,1 |
22,4 |
20,7 |
17,9 |
18,6 |
21,8 |
16,1 |
|
19,1 |
20,5 |
14,2 |
16,9 |
17,8 |
18,1 |
19,1 |
15,8 |
18,8 |
17,2 |
|
16,2 |
17,3 |
22,5 |
19,9 |
21,1 |
15,1 |
17,7 |
19,8 |
14,9 |
20,5 |
|
17,5 |
19,2 |
18,5 |
15,7 |
14,0 |
18,6 |
21,2 |
16,8 |
19,3 |
17,8 |
|
18,8 |
14,3 |
17,1 |
19,5 |
16,3 |
20,3 |
17,9 |
23,0 |
17,2 |
15,2 |
|
15,6 |
17,4 |
21,3 |
22,1 |
20,1 |
14,5 |
19,3 |
18,4 |
16,7 |
18,2 |
|
16,4 |
18,7 |
14,3 |
18,2 |
19,1 |
15,3 |
21,5 |
17,2 |
22,6 |
20,4 |
|
22,8 |
17,5 |
20,2 |
15,5 |
21,6 |
18,1 |
20,5 |
14,0 |
18,9 |
16,5 |
|
20,8 |
16,6 |
18,3 |
21,7 |
17,4 |
23,0 |
21,1 |
19,8 |
15,4 |
18,1 |
|
18,9 |
14,7 |
19,5 |
20,9 |
15,8 |
20,2 |
21,8 |
18,2 |
21,2 |
20,1 |
РЕШЕНИЕ
а) Записываем вариационный ряд. Располагаем значения результатов эксперимента в порядке возрастания.
|
14,0 |
14,0 |
14,2 |
14,3 |
14,3 |
14,5 |
14,7 |
14,9 |
15,1 |
15,2 |
|
15,3 |
15,4 |
15,5 |
15,6 |
15,7 |
15,8 |
15,8 |
15,9 |
16,1 |
16,2 |
|
16,3 |
16,4 |
16,5 |
16,6 |
16,7 |
16,8 |
16,9 |
17,1 |
17,1 |
17,2 |
|
17,2 |
17,2 |
17,3 |
17,4 |
17,4 |
17,5 |
17,5 |
17,7 |
17,8 |
17,8 |
|
17,9 |
17,9 |
18,1 |
18,1 |
18,1 |
18,2 |
18,2 |
18,2 |
18,3 |
18,4 |
|
18,5 |
18,6 |
18,6 |
18,7 |
18,8 |
18,8 |
18,9 |
18,9 |
19,1 |
19,1 |
|
19,1 |
19,1 |
19,2 |
19,3 |
19,3 |
19,5 |
19,5 |
19,8 |
19,8 |
19,9 |
|
20,1 |
20,1 |
20,2 |
20,2 |
20,3 |
20,4 |
20,5 |
20,5 |
20,5 |
20,7 |
|
20,8 |
20,9 |
21,1 |
21,1 |
21,2 |
21,2 |
21,3 |
21,4 |
21,5 |
21,6 |
|
21,7 |
21,8 |
21,8 |
22,1 |
22,4 |
22,5 |
22,6 |
22,8 |
23,0 |
23,0 |
б) Находим размах варьирования
.
.
По формуле
,
где
- число интервалов, вычисляем длину
частичного интервала:
.
В качестве границы первого интервала
возьмём
.
Границы следующих интервалов вычисляем
по формуле:
,
где
.
Находим середины интервалов:
.
Подсчитываем число значений результатов
эксперимента, попавших в каждый интервал,
т.е. находим частоты интервалов
.
Далее вычисляем относительные частоты
,
(
)
и их плотности
.
Все полученные результаты помещаем в
таблицу.
|
Номер
частичного интервала
|
Границы
интервала
|
Середина
интервала
|
Частота
интервала
|
Относительная
частота
|
Плотность
относительной частоты
|
|
1 2 3 4 5 6 7 8 9 |
14,0-15,0 15,0-16,0 16,0-17,0 17,0-18,0 18,0-19,0 19,0-20,0 20,0-21,0 21,0-22,0 22,0-23,0 |
14,5 15,5 16,5 17,5 18,5 19,5 20,5 21,5 22,5 |
8 10 9 15 16 12 12 11 7 |
0,08 0,1 0,09 0,15 0,16 0,12 0,12 0,11 0,07 |
0,08 0,1 0,09 0,15 0,16 0,12 0,12 0,11 0,07 |
|
|
- |
- |
100 |
1 |
1 |
в) Строим полигон частот и гистограмму относительных частот.
15
10
5
14,5 15,5 16,5 17,5 18,5 19,5 20,5 21,5 22,5
0,2
0,15
0,1
0,05
14 15 16
17 18 19 20 21 22 23
Находим значения эмпирической функции
распределения
.
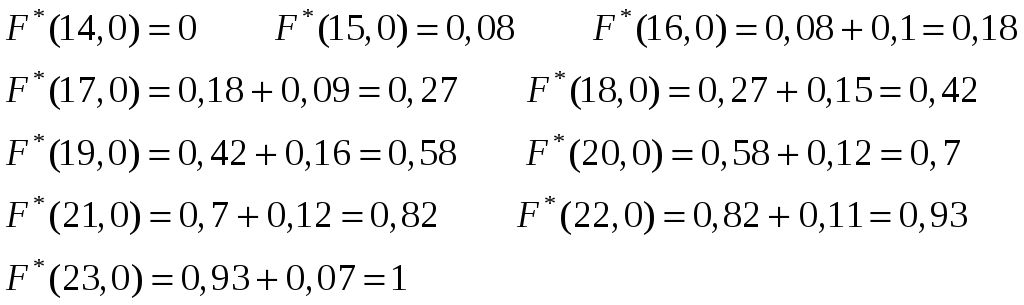
Строим график эмпирической функции распределения:
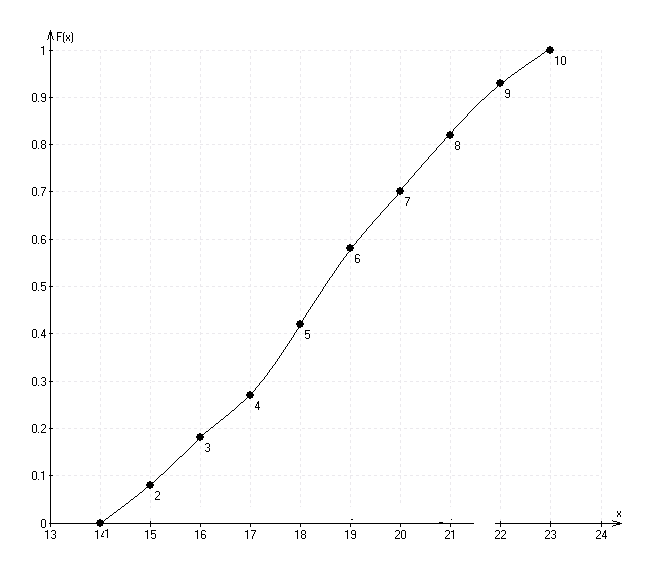
г) Найдём выборочное среднее
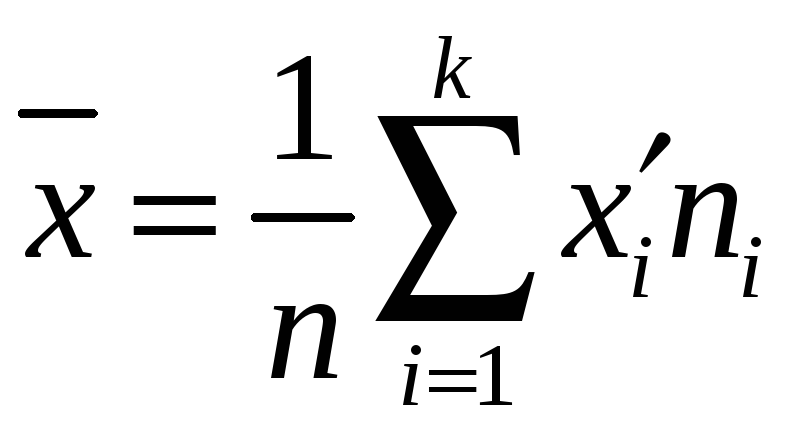и выборочную дисперсию
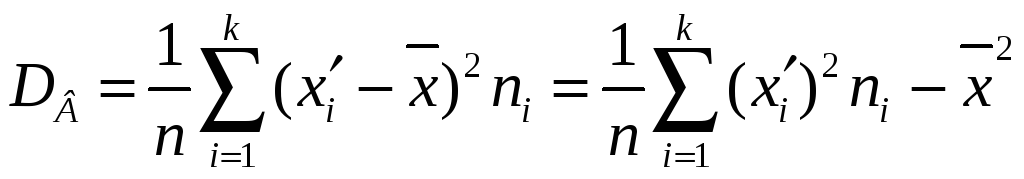
Составляем расчётную таблицу:
|
|
Границы
интервала
|
Середина
интервала
|
Частота
интервала
|
|
|
|
|
1 2 3 4 5 6 7 8 9 |
14,0-15,0 15,0-16,0 16,0-17,0 17,0-18,0 18,0-19,0 19,0-20,0 20,0-21,0 21,0-22,0 22,0-23,0 |
14,5 15,5 16,5 17,5 18,5 19,5 20,5 21,5 22,5 |
8 10 9 15 16 12 12 11 7 |
116 155 148,5 262,5 296 234 246 236,5 157,5 |
210,25 240,25 272,25 306,25 342,25 380,25 4202,25 462,25 506,25 |
1682 2402,5 2450,25 4593,75 5476 4563 5043 5084,75 3543,75 |
|
|
- |
- |
100 |
1852 |
|
34839 |
Находим выборочное среднее:
Находим выборочную дисперсию:
Находим выборочное среднее квадратическое отклонение:
Выборочная дисперсия является смещённой оценкой генеральной дисперсии, а исправленная дисперсия – несмещённой оценкой:
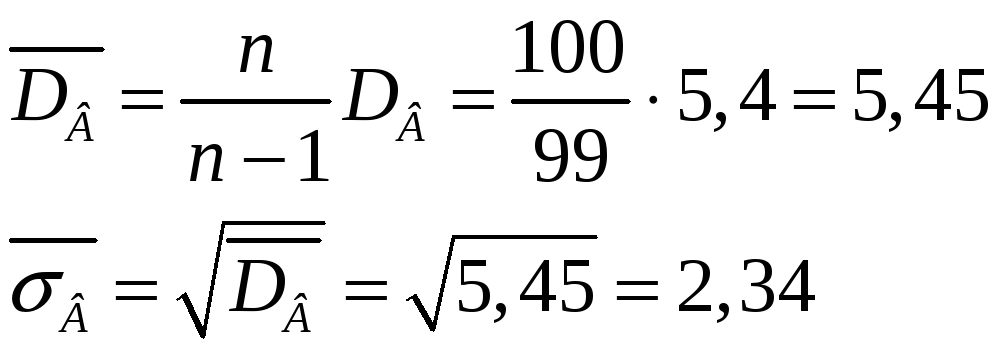
д) Согласно критерию Пирсона необходимо
сравнить эмпирические и теоретические
частоты. Эмпирические частоты даны.
Найдём теоретические частоты. Для этого
пронумеруем Х, т.е. перейдём к случайной
величине
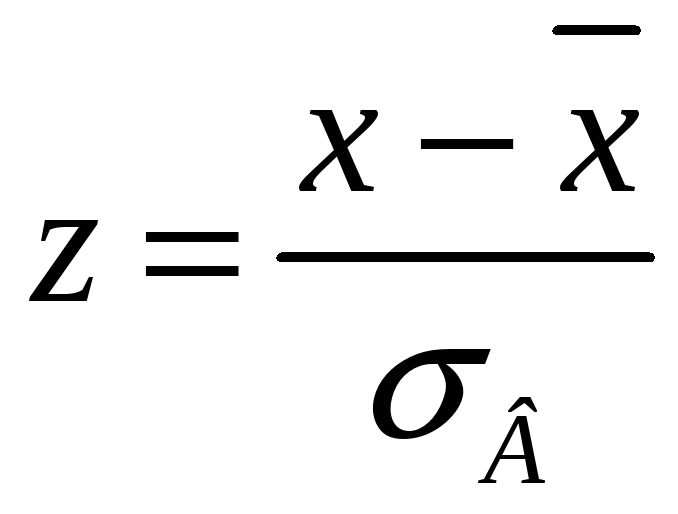и вычислим концы интервалов:
,
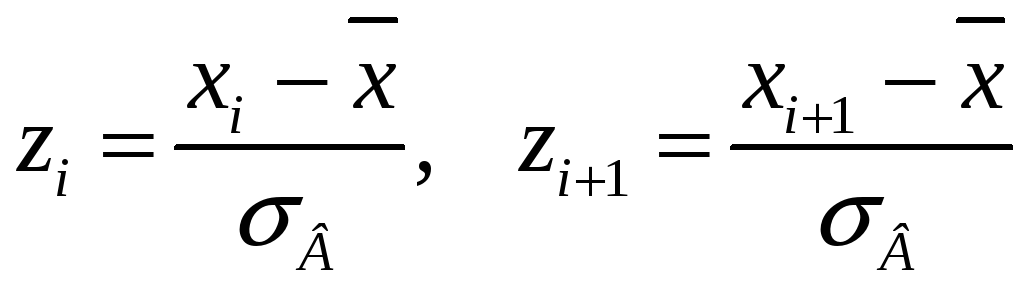причём наименьшее значение
,
точнее
положим стремящимся к
,
а наибольшее, точнее
- стремящемся к
.
Строим расчётную таблицу:
|
|
Границы интервала ( |
|
|
Границы интервала ( |
||
|
|
|
|
|
|||
|
1 2 3 4 5 6 7 8 9 |
14 15 16 17 18 19 20 21 22 |
15 16 17 18 19 20 21 22 23 |
- -3,52 -2,52 -1,52 -0,52 0,48 1,48 2,48 3,48 |
-3,52 -2,52 -1,52 -0,52 0,48 1,48 2,48 3,48 - |
- -1,52 -1,09 -0,66 -0,22 0,21 0,64 1,07 1,5 |
-1,52 -1,09 -0,66 -0,22 0,21 0,64 1,07 1,5 - |
)
)
Находим теоретические вероятности
и теоретические частоты:
.
Значения
и
находим по таблице Лапласа.
Составляем расчётную таблицу.
|
|
Границы интервала ( |
|
|
|
|
|
|
|
|
|||||
|
1 2 3 4 5 6 7 8 9 |
- -1,52 -1,09 -0,66 -0,22 0,21 0,64 1,07 1,5 |
-1,52 -1,09 -0,66 -0,22 0,21 0,64 1,07 1,5 - |
-0,5000 -0,4357 -0,3621 -0,2454 -0,0871 0,0832 0,2389 0,3577 0,4332 |
-0,4357 -0,3621 -0,2454 -0,0871 0,0832 0,2389 0,3577 0,4332 0,5000 |
0,0643 0,0736 0,1167 0,1583 0,1703 0,1557 0,1188 0,0755 0,0668 |
6,43 7,36 11,67 15,83 17,03 15,57 11,88 7,55 6,68 |
|
|
- |
- |
- |
- |
1 |
100 |
)
Вычислим наблюдаемое значение критерия Пирсона.
Для этого составляем расчётную таблицу.
Последние два столбца служат для контроля вычислений по формуле:
|
|
|
|
|
|
|
|
|
|
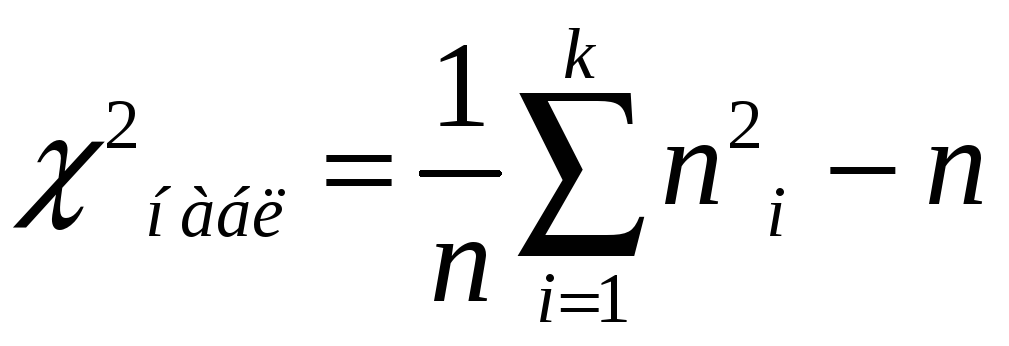
1 2 3 4 5 6 7 8 9 |
8 10 9 15 16 12 12 11 7 |
6,43 7,36 11,67 15,83 17,03 15,57 11,88 7,55 6,68 |
1,57 2,64 -2,67 -0,83 -1,03 -3,57 0,12 3,45 0,32 |
2,4649 6,9696 7,1289 0,6889 1,0609 12,7449 0,0144 11,9025 0,1024 |
0,3831 0,9467 0,6107 0,0431 0,0619 0,8176 0,0012 1,5791 0,0150 |
64 100 81 225 256 144 144 121 49 |
9,9533 13,5869 6,9409 14,2135 15,0323 9,2485 12,1212 16,0265 7,3353 |
|
|
100 |
100 |
- |
- |
|
- |
104,4584 |
4,4584Контроль:
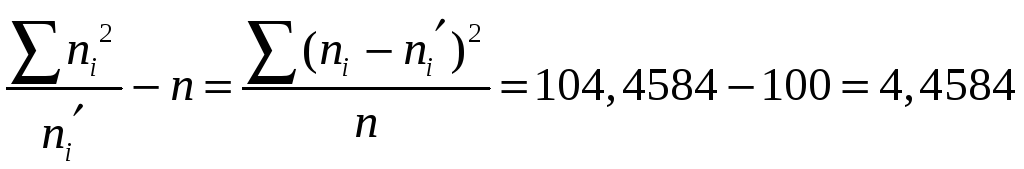
По таблице критических точек распределения
,
уровню значимости
и числу степеней свободы
(
- число интервалов) находим:
.