1.2.2. Графическое изображение множительной структуры

Основан на условном графическом изображении валов и передач. Проведем две вертикальных линии I и II (рис. 10, а). Отложим от линии 00 отрезки, равные lg n₁, lg n₂, lg n₃ ... Через точки 1, 2, 3, ... проведем горизонтальные линии. Вертикали I и II условно изображают валы, а точки 1, 2, 3, ... – их угловые скорости. Число точек на вертикальной линии указывает на количество угловых скоростей данного вала. Отрезки 1 – 2, 2 – 3, 3 – 4, … равны lg φ.

а)	б)

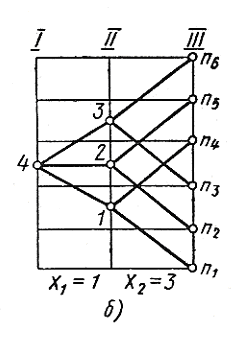
Рис. 10. Графическое изображение множительной структуры

Передачи условно изображают прямыми линиями – лучами (например, 6 – 5,6 – 3,6 – 1). Концы лучей соединяют с точками, соответствующими частотам вращения ведущего и ведомого валов. Луч6– I, например, изображает зубчатую передачу. Колесо сz₁вращается с валом I со скоростьюn₅, а колесо сz₂вращается с валом II cо скоростьюn₁.

Лучи с наклоном вверх (считая слева направо) изображают ускорительную передачу, а направленные вниз – замедляющую (редуцирующую) передачу. Передаточное отношение передачи i = φ±^s, где s – число интервалов (lg φ), на которое поднимается или опускается луч, изображающий передачу. Для ускорительной передачи s имеет положительное значение, для замедлительной – отрицательное. Пусть лучи 6 – 1, 6 – 3 и 6 – 5 (рис. 10, а) изображают для примера группу передач с трехвенцовым блоком (например, z₁ – z₂, z₃ – z₄, z₅ – z₆, рис. 9, а).

Тогда передаточное отношение передач согласно графику будет

.

Для каждой группы передач отводится пространство между двумя смежными вертикальными линиями I и II, называемое полем графика. В его пределах параллельные лучи (см. рис. 10, б) изображают одну и ту же передачу.

Характеристика группы х = s_x, где s_x – количество интервалов между соседними линиями, изображающими передачи данной группы. Например (рис. 10, а), для нашего случая между лучами 6 – 1, 6 – 3 и 6 – 5 заключено по два интервала, следовательно, х = 2. В самом деле, при работе передачи скорость вала I равна lgn₁, а переключая передачу на , получим lgn₃ = lg n₁ + 2lg φ = lg n₁ φ², т.е. увеличение скорости в φ^x = φ² раз.

Линия 00 и откладывание логарифмов частот вращения произведены для уяснения принципа. Обычно при построении графиков линию 00 не проводят, а точки 1, 2, 3, ... обозначают частоту вращения. Минимальное число вертикальных линий на графиках (по числу валов) равно m + 1, а горизонтальных (ступеней скорости) – z и больше. Передаточные отношения могут быть заданы также отношением диаметров шкивов ременных передач, дисков фрикционных передач и т.п.

Графический метод кинематического расчета состоит из двух частей: построения структурной сетки, характеризующей ряд конкретных приводов в общей форме, и по ней графика частот вращения, уточняющего расчет.

Построим структурную сетку для множительной структуры z = 6 = 3₁2₃ (см. рис. 9, а). Проведем три вертикальных линии, соответствующие валам I – III (рис. 10, б) и шесть горизонтальных линий, по количеству скоростей вала III. Наносим точки n₁ – n₆, изображающие ряд частот вращения последнего. Вал I имеет одну скорость, следовательно, на линии I должна быть одна точка (4). Располагаем ее симметрично, как указано на рисунке. Первая группа состоит из трех передач (z₁ – z₂, z₃ – z₄, z₅ – z₆), следовательно, из точки 4 необходимо провести три луча. Так как характеристика первой группы передач x₁ = 1, расстояние между соседними точками на линии II должно быть равно одному интервалу. Наносим симметрично точки 1, 2, 3 и соединяем их с точкой 1. Лучи 4 – 1, 4 – 2, 4 – 3 изображают передачи .

Проводим далее лучи, соответствующие двум передачам второй группы (z₇ – z₈, z₉ – z₁₀). Так как характеристика х₂ = 3, точку 1 соединяем с двумя равноудаленными от нее точками n₁ и n₄, стоящими одна от другой на расстоянии трех интервалов. Мы получили два луча 1 – n₁ и 1 – n₄. Поступаем аналогично с точками 2 и 3, соединяя их с точками n₂, n₅ и n₃, n₆. Один пучок параллельных лучей изображает передачу , другой – .

Характеризуя привод, структурные сетки являются общими для многих конкретных случаев, однако они не дают представления о частотах вращения валов и величине передаточных отношений передач. Поэтому для определения указанных параметров применительно к конкретным условиям привода строят так называемые графики частот вращения (картины скоростей).

В общем случае частота вращения приводного вала I n = n_maxφ^u, где n_max – верхний предел регулирования; u – любое число.

Для определения передаточных отношений передач необходимо по структурной сетке построить график частот вращения. Условием для задания передаточного отношения является предпочтительность передач 1 : 1.

С другой стороны, средством уменьшения радиальных размеров служит равенство , что приводит к симметричному расположению лучей. Используя для примера указанные условия в отношении структурной сетки, изображенной на рис. 10, б, точку 4 размещаем на уровне n₅, а точку 3 переносим на самый верх (рис. 11). Точки 1 – 2 располагаем, сохраняя расстояние их от точки 3, как на структурной сетке. Соединим по предыдущему точки лучами и, обозначив передачи, получим график частот вращения.

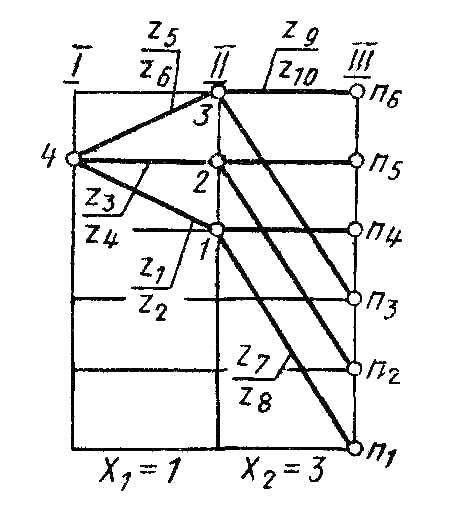
Рис. 11. График частот вращения

Передаточные отношения передач:

– первой группы

;

– второй группы

.

Практически принятые условия не всегда выполнимы. Поэтому по одной структурной сетке можно построить несколько вариантов графиков частот вращения.

Из всех возможных конструктивных и кинематических вариантов наивыгоднейшим следует признать тот, который обеспечивает наибольшую простоту, наименьшее количество передач и групп, малые радиальные и осевые размеры. Если z – число ступеней скорости, то наименьшее количество передач s_m = p_a + p_b +…+ p_m возможно при условии, если каждое слагаемое из правой части уравнения будет минимальным. Учитывая, что p_a, p_b, …, p_m – целые числа (больше единицы), минимальное значение могут иметь только простые числа – 2 и 3. Вот почему число передач в группах принимают равным 2 или 3, реже 4. При заданном z и минимальном количестве передач в группах увеличивается количество групп m, следовательно, и валов. При уменьшении числа групп возрастает количество передач в группах. Из всех возможных конструктивных и кинематических вариантов структуры с выбранным числом групп наивыгоднейшим следует признать тот, который обеспечивает наименьшие размеры и массу.

Масса зубчатых колес, смонтированных на одном вале, будет наименьшей при минимальной разнице в их размерах. Этим требованиям наилучшим образом отвечает основная группа, так как передаточные отношения передач здесь незначительно отличаются друг от друга. В силу этого целесообразна структура, у которой основная группа содержит наибольшее количество передач. Необходимо, чтобы р_a > р_b > … > p_m. Например, из трех вариантов z = 12 = 3·2·2 = 2·3·2 = 2·2·3 наилучшим является первый – z = 12 = 3·2·2; для z = 18 = 3·3·2 = 3·2·3 = 2·3·3 – вариант z =18 = 3·3·2.

Величина передаваемых ведомым валом крутящих моментов обратно пропорциональна величине передаточных отношений передач. Практически выгодно применять кинематический порядок, при котором минимальное передаточное отношение в группах уменьшается по мере приближения к шпинделю, достигая в последней группе предельного значения. В этом случае первые валы работают при более высоких скоростях, с меньшими нагрузками, имеют меньшие диаметры и модули зубчатых колес. Вместе с тем, промежуточные валы не должны работать при очень больших угловых скоростях, так как при этом возрастают потери холостого хода и износ деталей.

Указанные условия выполнимы, если первая группа будет основной, а характеристики переборных групп передач возрастают по мере приближения к шпинделю, т.е. x₁ < x₂ < … < x_m. Поэтому при построении графиков частот вращения необходимо следить за тем, чтобы минимальные значения передаточных отношений в группах постепенно уменьшались по мере приближения к шпинделю.

Отраслевой стандарт ОСТ2 Н11-1 рекомендует применять при проектировании станков в основном знаменатели ряда φ = 1,26; 1,41; 1,58. ГОСТ 8032 содержит ряды предпочтительных чисел, построенных в виде геометрических прогрессий, которые устанавливают предпочтительные величины и градации параметров в станкостроении, в том числе и ряды частот вращения и подач (табл. 6).

Таблица 6