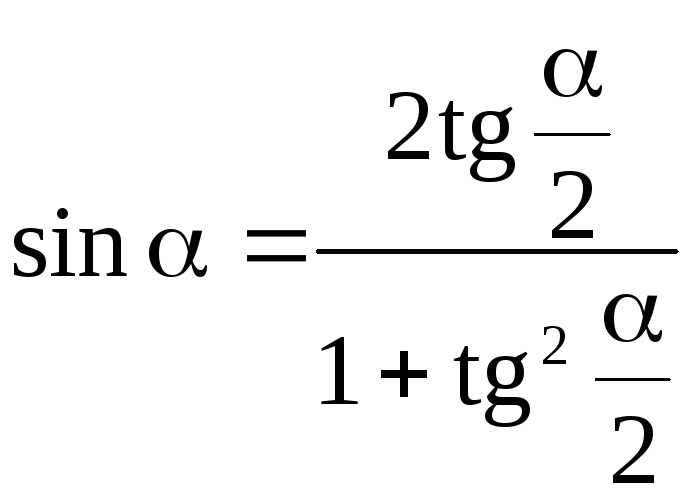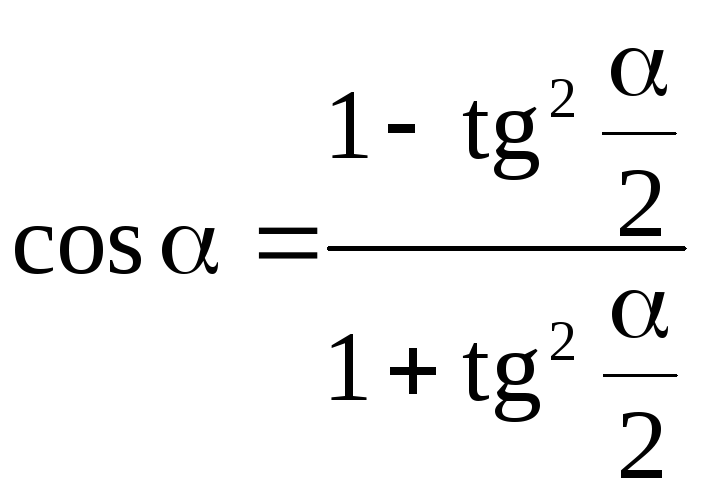Краткий теоретический справочник Модуль действительного числа. Свойства модулей

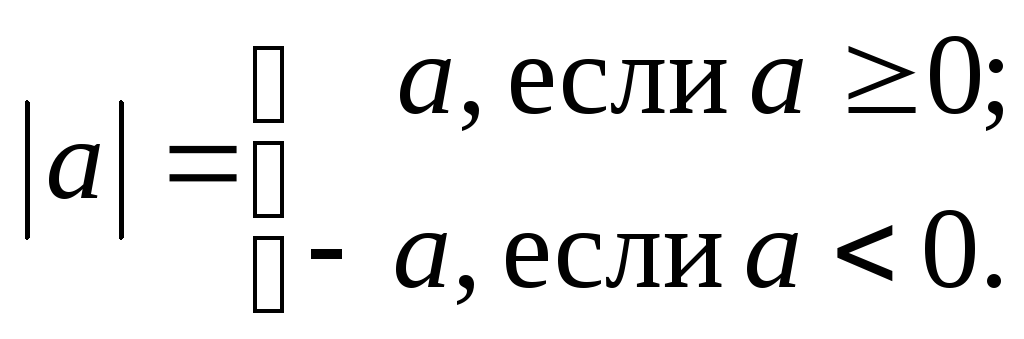
1. .	4. .	7. .
2. .	5. .	8. .
3. .	6. .	9. .

Степень действительного числа

, ,

если ; выражениене определено.

1.	4.
2.	5.
3.	6. ,

, если .

1.	5.
2.	6.
3.	7.
4. , если	8.

Формулы сокращенного умножения

Для :
Если нечетное ():
Бином Ньютона: , где - число сочетаний изпо.

Свойства логарифмов

.

Пусть .

1. Основное логарифмическое тождество:

.

2. Логарифм произведения, частного и степени:

; четное целое.

3. Формула перехода к новому основанию. Пусть 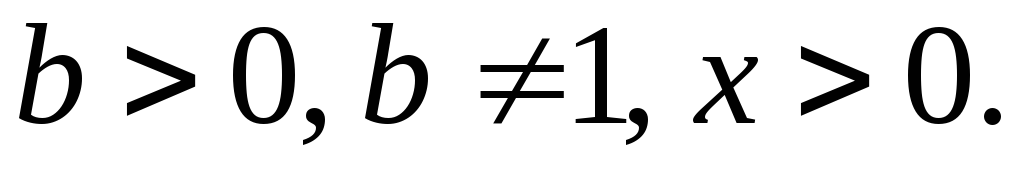Тогда

, в частности, , при.

Кроме того, .

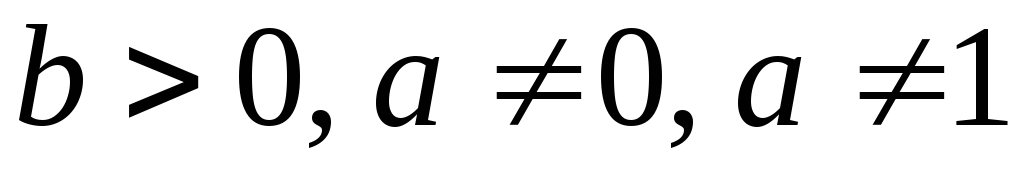4. Пусть , тогда

, ;,целое четное.

5. .

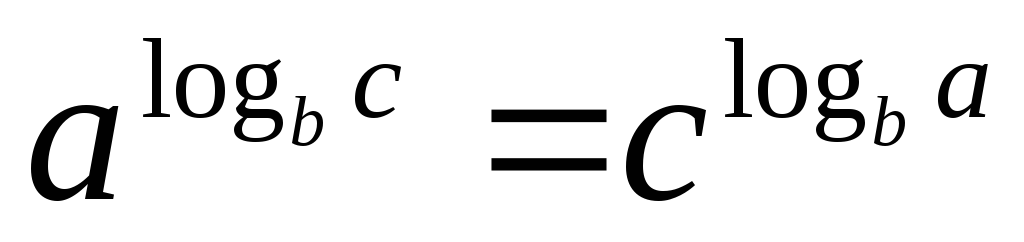6. Для любого положительного числа 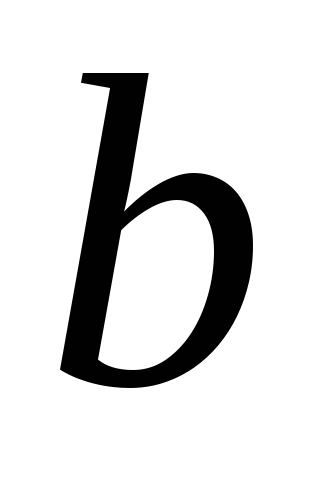существует, и притом только одно, такое действительное число, что.

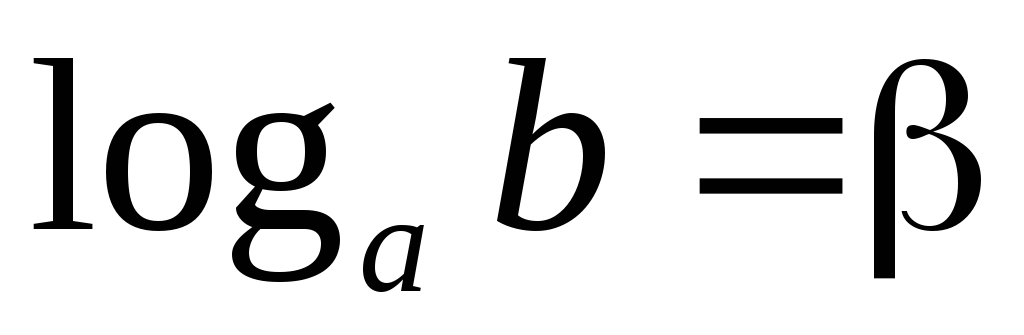7. Из равенства 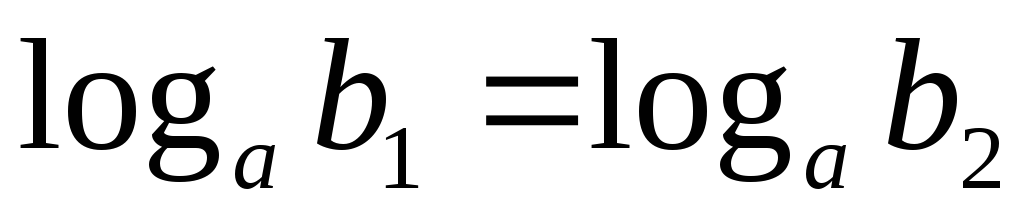следует, что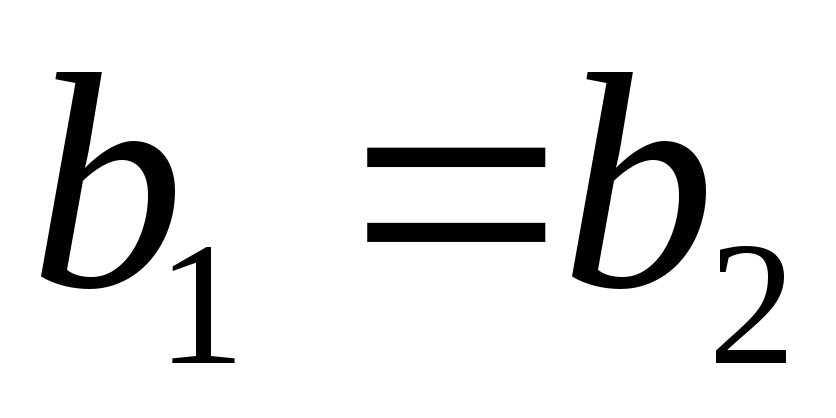(и наоборот).

Тригонометрия

Значение тригонометрических функций некоторых углов

	0
	0				1	0	-1
	1				0	-1	0
	0		1		-	0	-
	-		1		0	-	0

Основные тригонометрические тождества

Формулы суммы и разности аргументов

Формулы двойного и тройного аргументов

Выражение тригонометрических функций через тангенс половинного угла

Если ,, то

Преобразование суммы и разности тригонометрических

функций в произведение

Также бывает удобно использовать следующие преобразования.

где , аопределяется из формул;.

где , аопределяется из формул;.

Преобразование произведения тригонометрических функций в сумму

Формулы приведения

Справедливы следующие правила:

1. при переходе от функций углов ,к функциям угланазвание функции меняют на «ко-функцию»; при переходе от функций углов,к функциям углаимя функции не меняется;

2. знак определяется по функции, которую нужно преобразовать.

Функция	Аргумент

Определение обратных тригонометрических функций

;	;
;	.

Свойства обратных тригонометрических функций

, если
, если ;	, если

Некоторые значения обратных тригонометрических функций

	0				1	-1
	0
					0

	0		1
	0

Таблица квадратов

Дифференциальное исчисление функции одной переменной

Правила нахождения производной

Если у функций исуществуют производные, то

, где

Производная сложной функции

Если и существуют производныеи, то, где индексыиуказывают, по какому аргументу берутся производные.

Производные элементарных функций

№	Функция		№	Функция
1			11
2			12
3			13
4			14
5			15
6			16
7			17
8			18
9			19
10			20

Прогрессии

Арифметическая прогрессия

Если --й член,- разность,- суммапервых членов арифметической прогрессии, то

, ,,

.

Арифметическая прогрессия возрастает при и убывает при.

Если ,,,- члены арифметической прогрессии с такими номерами, что, то.

Для каждого члена арифметической прогрессии (кроме первого и последнего) выполнено соотношение:

.

Геометрическая прогрессия

Если --й член,- знаменатель,- суммапервых членов геометрической прогрессии, то

, ,;;,.

Если ,,,- члены геометрической прогрессии с такими номерами, что, то.

Для каждого члена геометрической прогрессии (кроме первого и последнего) выполнено соотношение:

.

Бесконечно убывающая геометрическая прогрессия

Если - сумма бесконечно убывающей геометрической прогрессии (), то

.

Геометрия

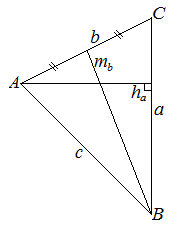
Треугольник
	Обозначения: - стороны; - противолежащие им углы;- высота к стороне;- медиана к стороне;- радиус вписанной окружности;- радиус описанной окружности;- площадь;- полупериметр. ; ; ; ; .

Признаки равенства треугольников

1. Если две стороны треугольника и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

2. Если сторона и два прилежащих к ним угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

3. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

Теорема о сумме углов в треугольнике. Сумма всех внутренних углов треугольника равна .

Равнобедренный треугольник

1. Углы при основании равнобедренного треугольника равны.

2. Если два угла треугольника равны, то такой треугольник равнобедренный.

3. В равнобедренном треугольнике высота, медиана и биссектриса, проведенные к основанию – совпадают.

Средняя линия треугольника – это отрезок, соединяющий середины сторон треугольника. Средняя линия треугольника параллельна основанию и равна ее половине.

Теоремы о медианах треугольника

1. Медианы треугольника пересекаются в одной точке и делятся ею в отношение 2:1, считая от вершины.

2. Медиана прямоугольного треугольника, проведенная из вершины прямого угла, равна половине гипотенузы.

Свойство серединных перпендикуляров к сторонам треугольника

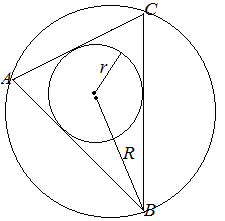
Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке, которая является центром окружности, описанной около треугольника.

Теорема о биссектрисах треугольника

Биссектрисы треугольника пересекаются в одной точке, которая является центром окружности, вписанной в треугольник.

Свойство биссектрисы треугольника

Биссектриса треугольника делит его сторону на отрезки, пропорциональные двум другим его сторонам.

Теорема косинусов. Квадрат стороны треугольника равен сумме квадратов двух других его сторон без удвоенного произведения этих сторон на косинус угла между ними.

Следствие из теоремы косинусов. Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.

Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов.

Равносторонний треугольник

Пусть - сторона треугольника, тогда

; ;;;.

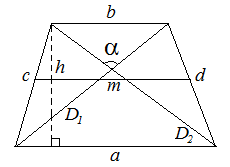
Трапеция
	Обозначения: - основания; - боковые стороны;- высота;- средняя линия;- диагонали;- угол между диагоналями;- площадь;- периметр. ; ; .
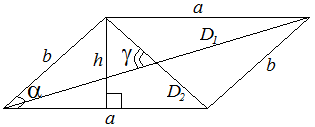
Параллелограмм
		Обозначения: - стороны; - высота;- средняя линия;- диагонали;- угол параллелограмма;- площадь;- угол между диагоналями. .
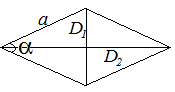
Ромб
		Обозначения: - сторона; - диагонали;- угол ромба;- площадь..