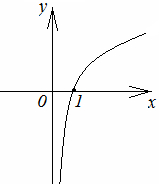- •Содержание
- •Предисловие
- •1. Числовые множества
- •1.1. Натуральные и целые числа
- •Способы нахождения наибольшего общего делителя (нод).
- •1.2. Рациональные числа
- •1.3. Иррациональные числа
- •1.4. Действительные числа. Числовые промежутки
- •1.5. Модуль действительного числа
- •Свойства модулей
- •1.6. Метод математической индукции
- •Задачи для самостоятельного решения Группа а
- •Группа b
- •Группа с
- •2. Функции действительного переменного
- •2.1. Понятие функции
- •Способы задания функции
- •2.2. Свойства функции Монотонность функции
- •Четные и нечетные функции
- •Свойства четных и нечетных функций
- •Периодические функции
- •Промежутки знакопостоянства и нули функции
- •Ограниченность функции
- •Свойства ограниченных функций
- •2.3. Основные элементарные функции
- •2.4. Элементарные функции. Классификация функций
- •Обратная функция
- •Сложная функция
- •Понятие элементарной функции
- •Классификация функций
- •2.5. Геометрические преобразования графиков функции
- •Задачи для самостоятельного решения Группа а
- •Группа b
- •Группа с
- •3. Степени. Многочлены. Корни. Алгебраические выражения
- •3.1. Степень действительного числа
- •3.2. Многочлены. Действия над многочленами
- •Действия над одночленами и многочленами
- •3.3. Преобразование алгебраических выражений
- •Задачи для самостоятельного решения Группа а
- •Группа b
- •Группа с
- •4. Уравнения
- •4.1. Основные понятия
- •4.2. Линейные уравнения
- •4.3. Квадратные уравнения и уравнения, сводящиеся к ним
- •Разложение квадратного трехчлена на множители
- •4.4. Рациональные и дробно-рациональные уравнения
- •4.5. Уравнения с модулем
- •4.6. Иррациональные уравнения
- •Задачи для самостоятельного решения Группа а
- •Группа b
- •Группа с
- •5. Неравенства
- •5.1. Основные понятия
- •5.2. Квадратные неравенства
- •5.3. Рациональные и дробно-рациональные неравенства. Метод интервалов для рациональных неравенств
- •5.4. Неравенства с модулем
- •5.5. Иррациональные неравенства
- •Задачи для самостоятельного решения Группа а
- •Группа b
- •Группа с
Свойства ограниченных функций
1. Если
![]() и
и![]() определены и ограничены на одном и том
же множестве
определены и ограничены на одном и том
же множестве![]() ,
то функции
,
то функции![]() ,
,![]() ,
,![]() ,
,![]() также ограничены на множестве
также ограничены на множестве![]() .
.
2. Если
![]() и
и![]() определены на множестве
определены на множестве![]() и функция
и функция![]() ограничена на этом множестве, а функция
ограничена на этом множестве, а функция![]() такова, что
такова, что![]() ,
то функция
,
то функция![]() ограничена на множестве
ограничена на множестве![]() .
.
2.3. Основные элементарные функции
Далее приведем наиболее важные свойства и графики основных элементарных функций.
|
Степенная функция | ||
|
|
1.
2.
3. нечетная, если
4. возрастает на
5. непериодическая; 6. неограниченная. |
|
|
|
1.
2.
3. нечетная, если
4. убывает на
5. непериодическая; 6. неограниченная.
|
|
|
|
1.
2.
3. нечетная, если
4. возрастает на
5. непериодическая; 6. нограниченная. |
|
|
Показательная функция | ||
|
|
1.
2.
3. общего вида;
4. возрастает на
5. непериодическая; 6. нограниченная. |
|
|
Логарифмическая функция | ||
|
|
1.
2.
3. общего вида;
4. возрастает на
5. непериодическая; 6. неограниченная. |
|
|
Тригонометрические функции | ||
|
|
1.
2.
3. нечетная;
4. возрастает на
5. периодическая, с периодом
6. ограниченная. |
|
|
2. |
1.
2.
3. четная;
4. возрастает на
убывает на
5. периодическая, с периодом
6. ограниченная. |
|
|
3.
|
1.
2.
3. нечетная; 4. возрастает на
5. периодическая, с периодом
6. неограниченная. |
|
|
4. |
1.
2.
3. нечетная;
4. возрастает на
5. периодическая, с периодом
6. неограниченная. |
|
|
Обратные тригонометрические функции | ||
|
1.
|
1.
2.
3. нечетная;
4. возрастает на
5. непериодическая; 6. ограниченная |
|
|
2.
|
1.
2.
3. общего вида;
4. убывает на
5. непериодическая; 6. ограниченная. |
|
|
3.
|
1.
2.
3. нечетная;
4. возрастает на
5. непериодическая; 6. ограниченная. |
|
|
4.
|
1.
2.
3. общего вида;
4. убывает на
5. непериодическая; 6. ограниченная. |
|