1.4. Действительные числа. Числовые промежутки

Если множество рациональных чисел объединить с множеством иррациональных чисел, то получится множество действительных чисел. Множество действительных чисел обычно означают буквой ; используют также символическую запись.

Действительные числа изображают точками координатной прямой (числовой оси).

Определение 1.8. Координатная прямая – это всякая прямая, на которой выбраны направление, принимаемое за положительное, точка – начало отсчета и единица измерения – масштабный отрезок, длина которого принимается равной единице.

Пусть и– действительные числа и. В таблице 1.1 даны названия, определения и обозначения числовых множеств, называемыхчисловыми промежутками, и их изображение на координатной прямой. Каждый из числовых промежутков определяется как множество действительных чисел , удовлетворяющих определенным неравенствам.

Таблица 1.1

Название	Неравенство, определяющее множество	Обозначение	Изображение
отрезок от до(замкнутый промежуток)
интервал от до(открытый промежуток)
открытый слева промежуток от до (полуинтервал)
открытый справа промежуток от до (полуинтервал)
числовой луч от до
открытый числовой луч от до
числовой луч от до
открытый числовой луч от до

1.5. Модуль действительного числа

Определение 1.9. Модулем неотрицательного действительного числа называют само это число: ; модулем отрицательного действительного числа называют противоположное число: .

Или записывают так:

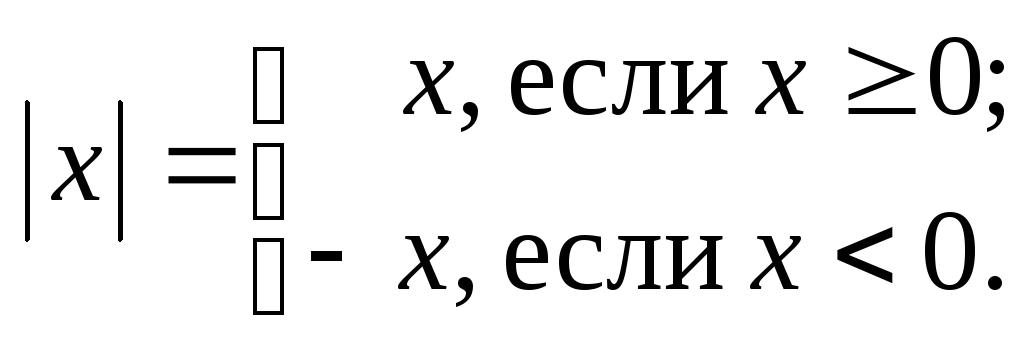
Например, ;;(так как).

Свойства модулей

1. .	4. .	7. .
2. .	5. .	8. .
3. .	6. .	9. .

1.6. Метод математической индукции

Утверждение, зависящее от натурального числа , справедливо для любого, если выполнены два условия:

1) утверждение верно для ;

2. из справедливости утверждения для 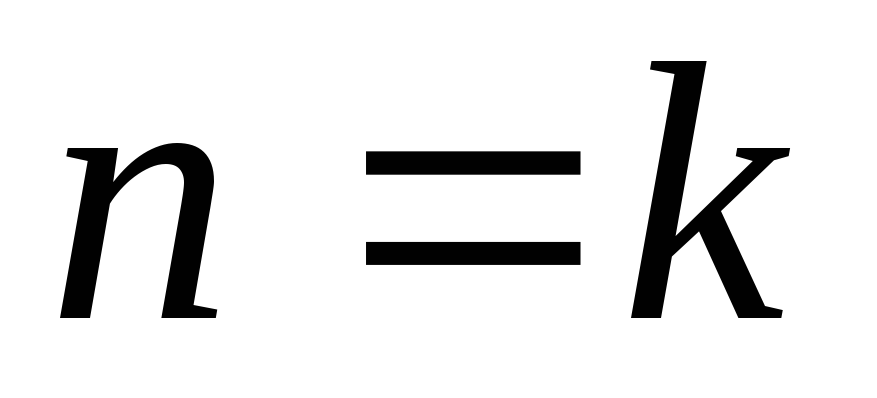, где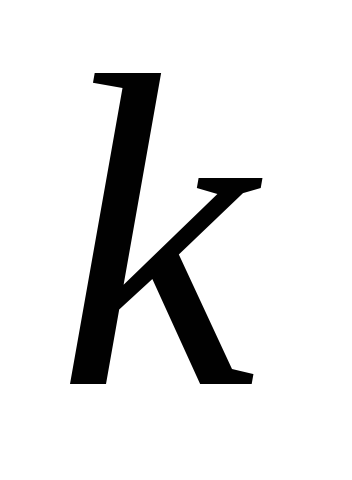– любое натуральное

число, вытекает справедливость утверждения и для следующего натурального числа .

Замечание 1.1. В некоторых случаях утверждение является истинным для , тогда в этом случае пункт1) проверяют для , а пункт2) доказывают при . Аналогично, если утверждение выполняется лишь для, тогда пункт1) проверяют для , а пункт2) доказывают при .

Пример 1.11. Доказать, что

.

(1.3)

Решение. 1) Проверим справедливость этого утверждения для , то есть справедливость равенства. Очевидно,.

2) Предположим, что равенство (1.3) выполняется при , то есть справедливо равенство:

.

(1.4)

Докажем, что тогда проверяемое равенство (1.3) верно и при , то есть докажем равенство

.

(1.5)

Подчеркнем, что равенство (1.5) интересует нас не само по себе, а интересует вопрос, вытекает ли оно из равенства (1.4).

Рассмотрим левую часть равенства (1.5) и воспользуемся в процессе преобразований равенством (1.4):

.

Таким образом, из равенства (1.4) вытекает равенство (1.5). Оба условия принципа математической индукции выполнены, следовательно, равенство (1.3) справедливо для любого натурального числа .

Пример 1.12. Доказать, что при

Решение. 1) При имеем:– делится на 17.

2) Предположим, что утверждение выполняется при , то есть, (, где), и докажем, что оно верно и при, а именно

.

Действительно,

.

Оба условия принципа математической индукции выполняются, следовательно, выдвинутое утверждение доказано.

Пример 1.13. Доказать, что для исправедливо неравенство

(его называют неравенством Бернулли в честь швейцарского математика Якоба Бернулли (1654-1705)).

Решение. 1) При получим верное неравенство:

(так как )

2) Предположим, что неравенство Бернулли верно для ():

.

(1.6)

Докажем, что неравенство Бернулли верно и для , то есть докажем, что

.

Умножим обе части неравенства (1.6) на одно и тоже положительное число , тогда получим:

,

что и требовалось доказать. Следовательно, по принципу математической индукции неравенство Бернулли справедливо для любого .