Группа b
Решить уравнение (1-20)
1.
.(Ответ:
.)
2.
.
(Ответ:
.)
3.
.
(Ответ:
.)
4.
.
(Ответ:
.)
5.
.
(Ответ:
.)
6.
.
(Ответ:
.)
7.
.
(Ответ:
.)
8.
.
(Ответ:
.)
9.
.
(Ответ:
.)
10.
.
(Ответ:
.)
11.
.
(Ответ:
.)
12.
.
(Ответ:
.)
13.
.
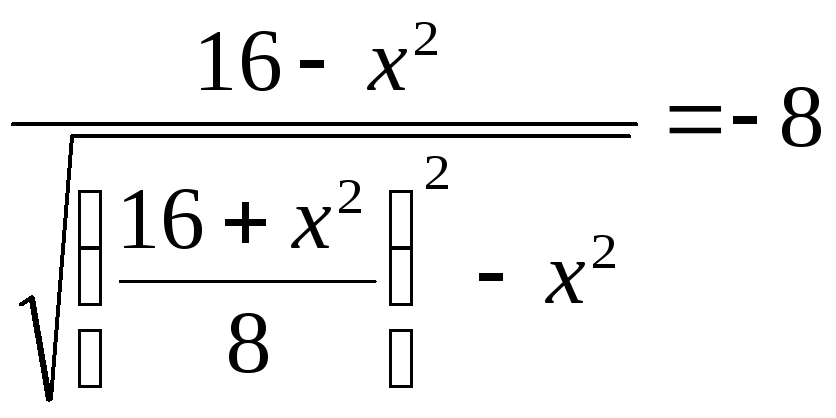(Ответ:
.)
14.
.
(Ответ:
.)
15.
.
(Ответ:
.)
16.
.
(Ответ:
.)
17.
.
(Ответ:
.)
18.
.
(Ответ:
.)
19.
.
(Ответ:
.)
20.
.
(Ответ:
;
.)
Группа с
Решить уравнение (1-10)
1.
.
(Ответ:
.)
2.
.
(Ответ:
.)
3.
.
(Ответ:
.)
4.
.
(Ответ:
.)
5.
.
(Ответ:
.)
6.
.
(Ответ:
.)
7.
.
(Ответ:
.)
8.
.
(Ответ:
.)
9.
.
(Ответ:
.)
10.
.
(Ответ:
.)
5. Неравенства
5.1. Основные понятия
Определение
5.1. Числовыми называются
неравенства вида
,
,
,
,
где
и
– числа или числовые выражения.
Определение
5.2. Неравенства
вида
,
,
,
называютсянеравенствами
с одной переменной.
Если неравенства
содержат знаки
или
,
то их называютстрогими,
а если знаки
или
–
нестрогими.
Определение 5.3. Значение переменной, при подстановке которого неравенство обращается в верное числовое неравенство, называется решением неравенства. Решить неравенство, значит найти все его решения или доказать, что их нет.
Определение 5.4. Равносильные неравенства – неравенства, множества решений которых совпадают.
При решении неравенств можно использовать следующие тождественные преобразования:
1. перенос слагаемых из одной части неравенства в другую, при этом их знак меняется на противоположный;
2. умножение (деление) обеих частей неравенства на положительное число, при этом знак неравенства сохраняется;
3. умножение (деление) обеих частей неравенства на отрицательное число, при этом знак неравенства меняется на противоположный.