3.3. Преобразование алгебраических выражений
Определение 3.8. Алгебраическим выражением называется выражение, составленное из чисел и переменных, знаков действия над ними (сложения, вычитания, умножения, деления, возведения в степень с рациональным показателем, извлечения арифметического корня) и скобок.
Два выражения называют тождественно равными, если при всех допустимых для них значениях переменных соответственные значения этих выражений равны. Замену одного выражения другим, тождественно равным ему выражением, называют тождественным преобразованием выражения.
Различают целые рациональные, дробные рациональные и иррациональные выражения. К целым рациональным выражениям относят одночлены и многочлены. Способы их преобразования были рассмотрены в пункте 3.2.
При тождественных преобразованиях дробных рациональных выражений (то есть содержащих деление на выражение с переменной) используются следующие основные приемы.
1. Сокращение
дробей, основанное на свойстве дроби:
.
Например,
,
(
).
2. Приведение к общему знаменателю – для этого необходимо:
1) разложить знаменатель каждой дроби на множители;
2) составить наименьший общий знаменатель;
3) домножив числитель и знаменатель каждой дроби на дополнительные множители, привести их к общему знаменателю.
Напомним, что действия над алгебраическими дробями осуществляются следующим образом
,
,
.
Пример 3.12. Упростить выражение
.
Решение.
,
(
).
Ответ:
,
(
).
Пример 3.13. Упростить выражение
.
Решение.
,
(
,
).
Ответ:
,
(
,
).
Рассмотрим далее преобразование иррациональных выражений. Выражение называется иррациональным, если оно содержит извлечение корня из переменной или возведение переменной в дробную степень. Как правило, тождественные преобразования выполняются на множестве неотрицательных чисел. При решении примеров мы будем это подразумевать и специально не оговаривать.
Пример 3.14.
Упростить
выражение
.
Решение.
.
Ответ:
.
Пример 3.15.
Упростить
выражение
.
Решение.
.
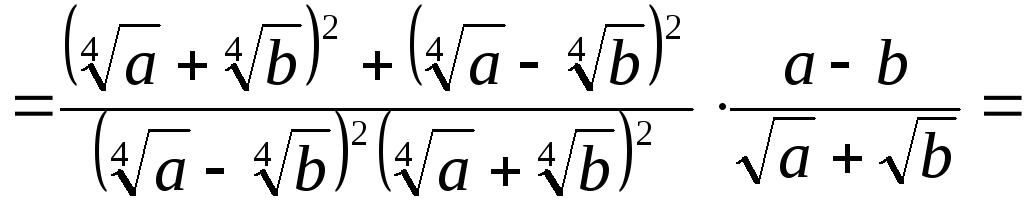
Избавимся от
иррациональности в знаменателе.
Для этого домножим числитель и знаменатель
на выражение, сопряженной к знаменателю,
то есть на сумму
.
Получим
.
Ответ:
.
Пример 3.16. Упростить выражение
.
Решение. Избавимся от иррациональности в знаменателе каждой из дробей в первой скобке:
,
.
Подстановка полученных выражений дает
.
Ответ:
.
Пример 3.17. Упростить выражение
.
Решение. Сделаем
замену
переменной
.
Тогда исходное выражение примет вид
.
Рассмотрим далее пример, содержащий произведение корней с различными показателями.
Ответ:
.
Пример 3.18.
Упростить
выражение
.
Решение.
.
Ответ:
.
Пример 3.19.
Вычислить
.
Решение. Заметим, что
,
тогда
=
.
Ответ: 6.
Пример 3.20.
Вычислить
.
Решение.
Так как
,
то
=
.
Ответ: 6.
Пример 3.21.
Вычислить
.
Решение.
.
Ответ:
.
Пример 3.22. Найти
значение выражения
при
.
Решение. Упростим предварительно заданное выражение
,
тогда при
получим
.
Ответ: 9.
Пример 3.22. Найти
значение выражения a)
,
б)
,
в)
.
Решение. а)
Представим оба подкоренных выражения
в виде полных квадратов:
и
,
тогда
.
б) Действуя аналогично пункту а), получаем
=
.
в)
.
Ответ: a)
;
б) 4; в) 3.
Пример 3.23.
Упростить
выражение
Решение. Проведем преобразования в ОДЗ
(
).
Ответ:
Пример 3.24.
Упростить
выражение
Решение.
Проведем
преобразования в ОДЗ
(
).
.
Ответ:
,
.
Пример 3.25. Упростить выражение
.
Решение. Воспользуемся равенством:
.
Тогда
.
Раскрывая скобки и приведя подобные, получаем
.
Ответ:
.