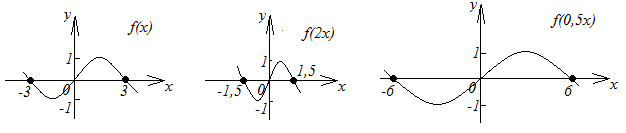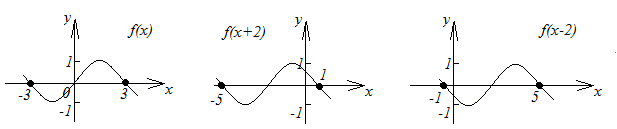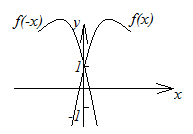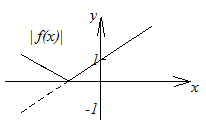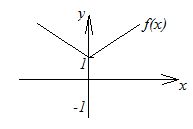- •Содержание
- •Предисловие
- •1. Числовые множества
- •1.1. Натуральные и целые числа
- •Способы нахождения наибольшего общего делителя (нод).
- •1.2. Рациональные числа
- •1.3. Иррациональные числа
- •1.4. Действительные числа. Числовые промежутки
- •1.5. Модуль действительного числа
- •Свойства модулей
- •1.6. Метод математической индукции
- •Задачи для самостоятельного решения Группа а
- •Группа b
- •Группа с
- •2. Функции действительного переменного
- •2.1. Понятие функции
- •Способы задания функции
- •2.2. Свойства функции Монотонность функции
- •Четные и нечетные функции
- •Свойства четных и нечетных функций
- •Периодические функции
- •Промежутки знакопостоянства и нули функции
- •Ограниченность функции
- •Свойства ограниченных функций
- •2.3. Основные элементарные функции
- •2.4. Элементарные функции. Классификация функций
- •Обратная функция
- •Сложная функция
- •Понятие элементарной функции
- •Классификация функций
- •2.5. Геометрические преобразования графиков функции
- •Задачи для самостоятельного решения Группа а
- •Группа b
- •Группа с
- •3. Степени. Многочлены. Корни. Алгебраические выражения
- •3.1. Степень действительного числа
- •3.2. Многочлены. Действия над многочленами
- •Действия над одночленами и многочленами
- •3.3. Преобразование алгебраических выражений
- •Задачи для самостоятельного решения Группа а
- •Группа b
- •Группа с
- •4. Уравнения
- •4.1. Основные понятия
- •4.2. Линейные уравнения
- •4.3. Квадратные уравнения и уравнения, сводящиеся к ним
- •Разложение квадратного трехчлена на множители
- •4.4. Рациональные и дробно-рациональные уравнения
- •4.5. Уравнения с модулем
- •4.6. Иррациональные уравнения
- •Задачи для самостоятельного решения Группа а
- •Группа b
- •Группа с
- •5. Неравенства
- •5.1. Основные понятия
- •5.2. Квадратные неравенства
- •5.3. Рациональные и дробно-рациональные неравенства. Метод интервалов для рациональных неравенств
- •5.4. Неравенства с модулем
- •5.5. Иррациональные неравенства
- •Задачи для самостоятельного решения Группа а
- •Группа b
- •Группа с
2.5. Геометрические преобразования графиков функции
Если известен
график функции
![]() ,
то с помощью некоторых преобразований
плоскости (параллельного переноса,
осевой и центральной симметрии и т. п.)
можно построить графики более сложных
функций.
,
то с помощью некоторых преобразований
плоскости (параллельного переноса,
осевой и центральной симметрии и т. п.)
можно построить графики более сложных
функций.
1. График функции
![]() получается сжатием графика функции
получается сжатием графика функции
![]() в
в
![]() раз к оси
раз к оси![]() при
при![]() или растяжением в
или растяжением в![]() раз от этой оси
раз от этой оси![]() при
при![]() (рисунок 2.12).
(рисунок 2.12).
|
|
|
рис. 2.12 |
2. График функции
![]() получается параллельным переносом
графика
получается параллельным переносом
графика
![]() в отрицательном направлении оси
в отрицательном направлении оси
![]() на
на![]() при
при![]() и в положительном направлении на
и в положительном направлении на![]() при
при![]() (рисунок 2.13).
(рисунок 2.13).
|
|
|
рис. 2.13 |
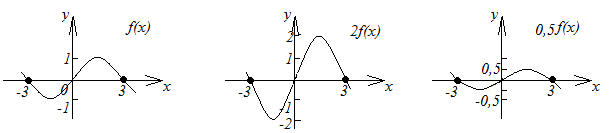
3. График функции
![]() получается растяжением графика функции
получается растяжением графика функции![]() вдоль оси
вдоль оси![]() в
в![]() раз при
раз при![]() и сжатием вдоль этой оси в
и сжатием вдоль этой оси в![]() раз при
раз при![]() (рисунок 2.14).
(рисунок 2.14).
|
|
|
рис. 2.14 |
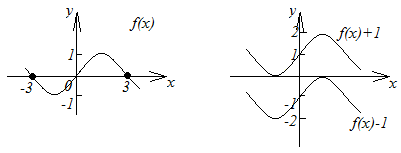
4. График функции
![]() получается параллельным переносом
графика
получается параллельным переносом
графика![]() в положительном направлении оси
в положительном направлении оси![]() на
на![]() при
при![]() и в отрицательном направлении этой оси
на
и в отрицательном направлении этой оси
на![]() при
при![]() (рисунок 2.15).
(рисунок 2.15).
|
|
|
|
рис. 2.15 |
рис. 2.16 |
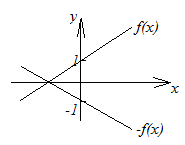
5. График функции
![]() получается симметричным отображением
графика
получается симметричным отображением
графика![]() относительно оси
относительно оси![]() (рисунок 2.16).
(рисунок 2.16).
6. График функции
![]() получается симметричным отображением
графика
получается симметричным отображением
графика![]() относительно оси
относительно оси![]() (рисунок 2.17).
(рисунок 2.17).
7. График функции
![]() получается из графика функции
получается из графика функции![]() следующим образом: часть графика
следующим образом: часть графика![]() ,
лежащая над осью
,
лежащая над осью![]() ,
сохраняется, часть его, лежащая под осью
,
сохраняется, часть его, лежащая под осью![]() ,
отображается симметрично относительно
оси
,
отображается симметрично относительно
оси![]() (рисунок 2.18).
(рисунок 2.18).
|
|
|
|
|
рис. 2.17 |
рис. 2.18 |
рис. 2.19 |
8. График функции
![]() получается из графика функции
получается из графика функции![]() следующим образом: часть графика функции
при
следующим образом: часть графика функции
при![]() график
график![]() сохраняется, а при
сохраняется, а при![]() полученная часть графика отображается
симметрично относительно оси
полученная часть графика отображается
симметрично относительно оси![]() (рисунок 2.19).
(рисунок 2.19).
Задачи для самостоятельного решения Группа а
Найти область
определения функции
![]() (1-4)
(1-4)
1.
![]() .
(Ответ:
.
(Ответ:
![]() .)
.)
2.
![]() .
(Ответ:
.
(Ответ:
![]() .)
.)
3.
![]() .
(Ответ:
.
(Ответ:
![]() .)
.)
4.
![]() .
(Ответ:
.
(Ответ:
![]() .)
.)
Найти множество
значений функции
![]() (5-9)
(5-9)
5.
![]() .
(Ответ:
.
(Ответ:
![]() .)
.)
6.
![]() .
(Ответ:
.
(Ответ:
![]() .)
.)
7.
![]() .
(Ответ:
.
(Ответ:
![]() .)
.)
8.
![]() .
(Ответ:
.
(Ответ:
![]() .)
.)
9.
![]() .
(Ответ:
.
(Ответ:
![]() .)
.)
Найти нули функции
![]() (10-14)
(10-14)
10.
![]() .
(Ответ:
.
(Ответ:
![]() .)
.)
11.
![]() .
(Ответ:
.
(Ответ:
![]() .)
.)
12.
![]() .
(Ответ:
.
(Ответ:
![]() .)
.)
13.
![]() .
(Ответ:
.
(Ответ:
![]() .)
.)
14.
![]() .
(Ответ:
.
(Ответ:
![]() .)
.)
15. Дана функция
![]() .
Найти:
.
Найти:![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() .
.
16. Дана функция
![]() .
Найти:
.
Найти:![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() .
.
17. Дана функция
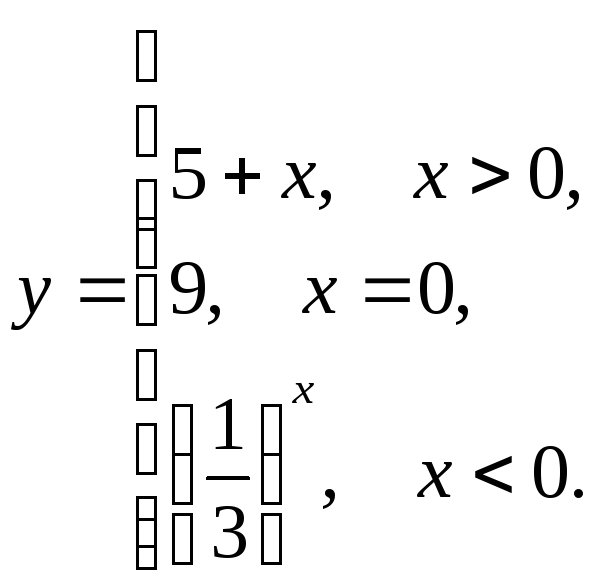 Найти:
Найти:![]() ;
;![]() ;
;![]() ;
;![]() .
.
18. Найти
![]() ,
,![]() ,
,![]() ,
,![]() ,
если
,
если
а)
![]() ,
,![]() ;
;
б)
![]() ,
,![]() .
.
Исследовать на
четность-нечетность функции
![]() (19-27)
(19-27)
19.
![]() .
(Ответ:
четная.)
.
(Ответ:
четная.)
20.
![]() .
(Ответ:
четная.)
.
(Ответ:
четная.)
21.
![]() .
(Ответ:
четная.)
.
(Ответ:
четная.)
22.
![]() .
(Ответ:
нечетная.)
.
(Ответ:
нечетная.)
23.
![]() .
(Ответ:
нечетная.)
.
(Ответ:
нечетная.)
24.
![]() .
(Ответ:
нечетная.)
.
(Ответ:
нечетная.)
25.
![]() .
(Ответ:
нечетная.)
.
(Ответ:
нечетная.)
26.
![]() .
(Ответ:
четная.)
.
(Ответ:
четная.)
27.
![]() .
(Ответ:
общего вида.)
.
(Ответ:
общего вида.)
Найти функцию,
обратную данной функции
![]() (28-29)
(28-29)
28.
![]() ,
,![]() .
(Ответ:
.
(Ответ:
![]() ,
,![]() .)
.)
29.
![]() ,
,![]() .
(Ответ:
не имеет
обратной функции.)
.
(Ответ:
не имеет
обратной функции.)
Выяснить, является
ли функция
![]() периодической и в случае периодичности
указать ее наименьший период (30-37)
периодической и в случае периодичности
указать ее наименьший период (30-37)
30.
![]() .
(Ответ:
.
(Ответ:
![]() .)
.)
31.
![]() .
(Ответ:
.
(Ответ:
![]() .)
.)
32.
![]() .
(Ответ:
.
(Ответ:
![]() .)
.)
33.
![]() .
(Ответ:
.
(Ответ:
![]() .)
.)
34.
![]() .
(Ответ:
.
(Ответ:
![]() .)
.)
35.
![]() .
(Ответ:
непериодическая.)
.
(Ответ:
непериодическая.)
36.
![]() .
(Ответ:
непериодическая.)
.
(Ответ:
непериодическая.)
37.
![]() .
(Ответ:
непериодическая.)
.
(Ответ:
непериодическая.)