Тождественность микрочастиц и принцип Паули

Принцип неразличимости микрочастиц. Не существует физических различий между микрочастицами одной природы, имеющими одинаковый набор квантовых чисел. В квантовой механике вне области применимости квазиклассического приближения нет понятия траектории и невозможно проследить за частицей. Специальное выделение частицы изменяет ее физическое состояние. В результате попарная перестановка тождественных микрочастиц системы не изменяет ее физические характеристики.

Фермионы и бозоны. Спиновое квантовое число , определяющее проекцию спина частицы, рассматриваем наряду с ее координатой. Такое объединение описывает обобщенная координата

.

Состояние частицы с набором квантовых чисел n описывает функция .Состояние двух частиц системы описывает функция

.

При взаимной перестановке частиц переставляются их обобщенные координаты. Согласно принципу неразличимости частиц плотность вероятности при этом не изменяется

.

Такие состояния могут отличаться только фазовым множителем

.

Повторная перестановка восстанавливает исходное состояние, тогда

, ,

в результате

. (7.38)

Симметричной функцией описываются частицы бозоны, антисимметричной функцией описываются фермионы. Название частицам дал Поль Дирак в 1947 г. в честь Энрико Ферми и Шатьендраната Бозе, установивших статистические распределения соответствующих частиц. В квантовой теории поля из условия положительности энергии Паули доказал, что спин фермиона полуцелый, спин бозона целочисленный. Электроны относятся к фермионам, и волновая функция системы электронов меняет знак при взаимной перестановке любой пары частиц. К бозонам относятся, например, фотоны, имеющие единичный спин и симметричную функцию состояния.

Определитель Слэтера. Рассмотрим систему двух фермионов с перекрывающимися волновыми функциями. Частица идентифицируется по ее обобщенной координате . У одного фермиона набор квантовых чиселn₁, у другого – n₂. Волновая функция системы антисимметрична при перестановке обобщенных координат частиц

.

Этим свойством обладает суперпозиция функций отдельных частиц

,

где – состояние частицы 1 с набором квантовых чисел; множительобеспечивает нормировку. Заменапереставляет столбцы определителя, и он меняет знак. Обобщением дляN фермионов является определитель Слэтера

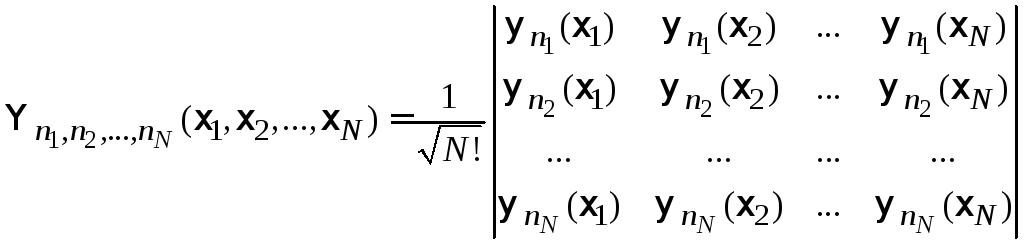. (7.39)

Перестановка любой пары частиц соответствует перестановке соответствующих столбцов определителя, и он меняет знак. Определитель (7.40) предложил Джон Слэтер в 1929 г.

Система бозонов описывается симметризованной функцией. Например для двух частиц

.

Принцип запрета Паули. Если наборы квантовых чисел, например n₁ и n₂, совпадают, то две строки определителя Слэтера (7.39) одинаковые и он равен нулю. В результате в системе фермионов не существует двух или более частиц с одинаковым набором квантовых чисел. Состояния фермионов, входящих в систему, должны отличаться хотя бы по одному квантовому числу. Принцип установил Паули в 1924 г.

Вольфганг Паули (1900–1958)

Принцип Паули, в частности, запрещает нескольким электронам в одном состоянии двигаться одновременно через резистор, находящийся под напряжением U. Такие электроны проходят резистор периодически с периодом τ, который можно оценить при помощи соотношения неопределенностей время-энергия . Приполучаем интервалмежду прохождениями электронов в одинаковых состояниях.