
Уравнение Паули
С магнитным полем В взаимодействует спиновый магнитный момент электрона
![]() ,
,
где
 – магнетон Бора;g
– множитель Ланде. Гамильтониан
взаимодействия
– магнетон Бора;g
– множитель Ланде. Гамильтониан
взаимодействия
![]() .
.
С учетом взаимодействия уравнение Шредингера переходит в уравнение, полученное Вольфгангом Паули в 1927 г.
Гамильтониан
электрона с зарядом
![]() в магнитном поле с
векторным потенциалом А
без учета спина имеет вид
в магнитном поле с
векторным потенциалом А
без учета спина имеет вид
 .
.
С учетом взаимодействия спина с магнитным полем получаем гамильтониан Паули в матричной форме
![]() ,
(7.20)
,
(7.20)
где
 ,
,
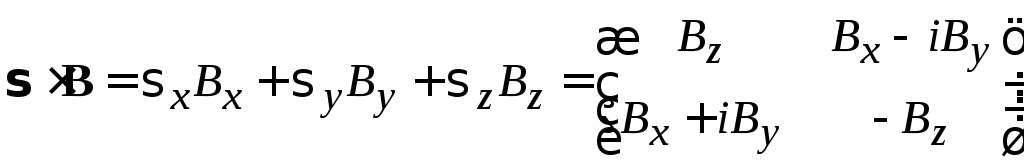 .
(7.21)
.
(7.21)
Уравнение Паули. Подставляем (7.20) в волновое уравнение Шредингера
![]() ,
,
получаем уравнение Паули
 (7.22)
(7.22)
для
спинора
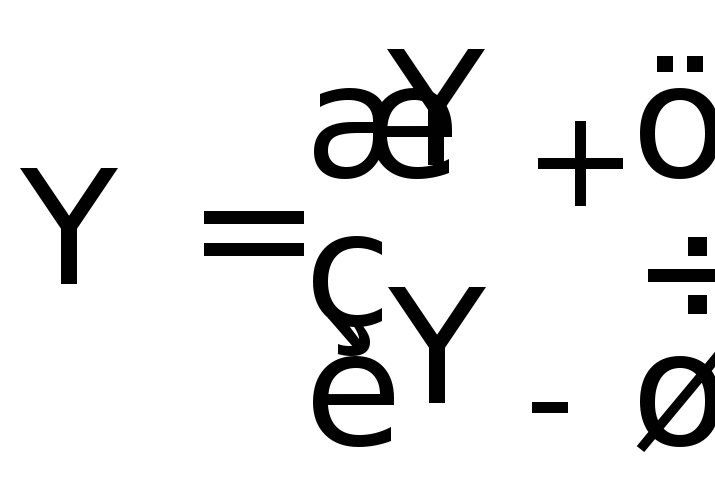 ,
где
,
где![]() – состояния с проекциями спина
– состояния с проекциями спина![]() на осьz.
Рассмотрим частный случай.
на осьz.
Рассмотрим частный случай.
Однородное
поле В.
Слагаемое
![]() в (7.22) не зависит от спина, а
в (7.22) не зависит от спина, а![]() не зависит от координат, поэтому спиновые
и координатные переменные разделяются
не зависит от координат, поэтому спиновые
и координатные переменные разделяются
![]() ,
,
где
![]() –координатная
функция;
–координатная
функция;
 –спиновая
функция;
–спиновая
функция;
![]() –состояния
с проекциями спина
–состояния
с проекциями спина
![]() на осьz.
на осьz.
Делим
(7.22) слева на ![]()
 ,
,
подставляем
![]() ,
и получаем
,
и получаем
 .
.
Уравнения для координатной и спиновой функций разделяются, получаем традиционное уравнение для координатной функции
![]() ,
(7.23)
,
(7.23)
и уравнение для спинора
![]() .
(7.24)
.
(7.24)
Взаимодействие
спина с однородным магнитным полем не
влияет на координатную часть волновой
функции
![]() .
.
При
![]() спиновая функция не зависит от времени.
спиновая функция не зависит от времени.
При
![]() используем
(7.21)
используем
(7.21)
 ,
,
 .
.
Для
спиновых функций ![]() с противоположными проекциями спина
на ось z
из (7.24) получаем
с противоположными проекциями спина
на ось z
из (7.24) получаем
 (7.25)
(7.25)
Направляем
ось z
вдоль поля, тогда
![]() ,
,![]() и уравнения разделяются
и уравнения разделяются
![]() ,
(7.26)
,
(7.26)
где спиновый сдвиг энергии
![]() .
.
Стационарное состояние. Если магнитное поле В и потенциальная энергия U не зависят от времени, тогда из (7.23) и (7.26) следует, что состояния
![]()
удовлетворяют стационарному уравнению Шредингера
![]() .
.
Учитывая
![]() ,
,
получаем
![]() .
(7.27)
.
(7.27)
Если спин электрона направлен по полю, то его спиновый магнитный момент – против поля и энергия состояния изменяется на
![]() .
.
Если спин направлен против поля, то магнитный момент – по полю и энергия состояния изменяется на
![]() .
.
Однородное
стационарное магнитное поле расщепляет
уровень энергии, снимая вырождение по
спиновому числу
![]() .
Расщепление в магнитном поле уровней
атома с разными значениями магнитного
квантового числа и нулевым спином
исследовал Зееман в 1896 г. Спиновое
расщепление
.
Расщепление в магнитном поле уровней
атома с разными значениями магнитного
квантового числа и нулевым спином
исследовал Зееман в 1896 г. Спиновое
расщепление
![]()
называется аномальным эффектом Зеемана. Его описал Ланде в 1922 г.

Спиновое расщепление уровня


Питер Зееман Альфред Ланде
(1865–1943) (1888–1976)
Найдем поведение вектора спина с течением времени в однородном стационарном магнитном поле. Уравнению спиновых функций (7.26)
![]()
удовлетворяют
![]() ,
,
![]() ,
,
где
 ;
(7.28)
;
(7.28)
 –циклотронная
частота. Получаем спиновую функцию
–циклотронная
частота. Получаем спиновую функцию
 (7.29)
(7.29)
с условием нормировки
![]() .
.
Ищем среднюю проекцию спина (7.15)
![]() .
.
Используя
 ,
,
 ,
,
и (7.29), получаем
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
(7.30)
,
(7.30)
где использованы проекции в начальный момент
![]() ,
,
![]() .
.
В
постоянном магнитном поле сохраняется
средняя проекция спина электрона на
направление поля, вектор спина вращается
вокруг направления поля с частотой
![]() .
.
При
![]() вектор спина находится в плоскости
(x,y)
и в начальный момент направлен вдоль
оси x.
С течение времени спин вращается вокруг
оси z
по часовой стрелки, если смотреть вдоль
вектора магнитного поля, частота
прецессии при
вектор спина находится в плоскости
(x,y)
и в начальный момент направлен вдоль
оси x.
С течение времени спин вращается вокруг
оси z
по часовой стрелки, если смотреть вдоль
вектора магнитного поля, частота
прецессии при
![]() равна циклотронной частоте. Вектор
спина дырки, имеющей положительный
заряд, вращается в противоположную
сторону. При
равна циклотронной частоте. Вектор
спина дырки, имеющей положительный
заряд, вращается в противоположную
сторону. При![]() ,
,![]() спин направлен вдоль магнитного поля,
вращение отсутствует.
спин направлен вдоль магнитного поля,
вращение отсутствует.
