Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Новосибирский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Лекции Квант.мех. СГФ / Квант. мех

..pdf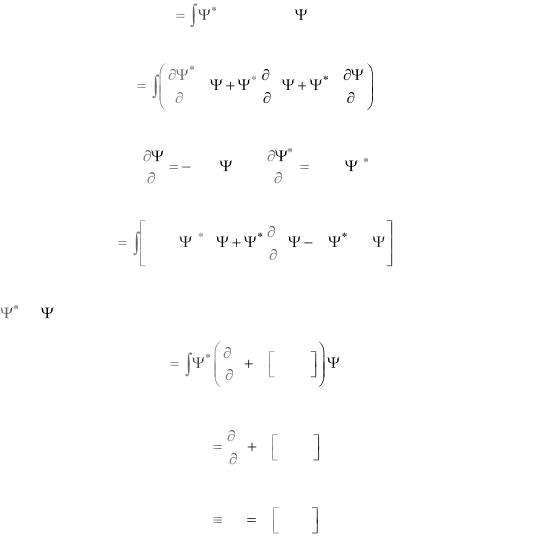

Скачиваний:

239

Добавлен:

11.03.2016

Размер:

13.88 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 366 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

2.9. Быстрота изменения величины

2.9. БЫСТРОТА ИЗМЕНЕНИЯ ВЕЛИЧИНЫ

Среднее значение физической величины изменяется со временем из-за зависимости ее оператора от времени и за счет некоммутативности оператора с гамильтонианом.

Оператор производной по времени. Для среднего значения (2.28)

величины, описываемой оператором

A(r, t)

a (t)

(r, t) A(r, t) (r, t) dV ,

находим быстроту изменения

dV .

Используя уравнение Шрѐдингера (2.54)

)

получаем

ˆ ˆ

(H ) A

dV .

Гамильтониан эрмитов, тогда первое слагаемое в квадратных скобках равно

i	ˆ ˆ	и
	HA	и

da	ˆ	i
da	A	i	ˆ	ˆ
dt	t		H , A		dV .	(2.66)

В результате оператор производной по времени

ˆ	ˆ	i
dA	A	i	ˆ	ˆ
dt	t		H , A .		(2.67)

Например, для оператора проекции скорости

vˆx	dxˆ	i	ˆ	(2.67а)
vˆx	dt		H , x	(2.67а)
	dt

Глава 2. МАТЕМАТИЧЕСКИЙ АППАРАТ КВАНТОВОЙ МЕХАНИКИ

используем (2.53)

d 2

и находим

vˆx

d 2

, x .

dx2

U (x, t)

dx2

d 2

В задаче 1.16 получено

, x

, тогда оператор скорости

dx2

vˆx

1 d

pˆ x

(2.67б)

i dx

удовлетворяет классическому соотношению между скоростью и импульсом, подтверждая правило сопоставления.

Сохраняющаяся величина		описывается оператором				ˆ
Сохраняющаяся величина		описывается оператором				A , удовлетво-
	ˆ		i
ряющим согласно (2.67) условию	A		i	ˆ ˆ	0 . Если оператор не зависит
ряющим согласно (2.67) условию	t			[H , A]	0 . Если оператор не зависит
ˆ
от времени A / t 0 , то
	ˆ	ˆ		0 .		(2.68)
	H, A			0 .		(2.68)

Величина сохраняется в любом состоянии, если ее оператор не зависит от времени и коммутирует с гамильтонианом.

Стационарное состояние характеризуется тем, что для величины a,

описываемой оператором	ˆ			ˆ	среднее
	A , не зависящим от времени A / t 0 ,
значение постоянно da / dt	0 . Если	ˆ	ˆ	0 , то из (2.66) получаем
		[H, A]
	ˆ	ˆ	dV	0	(2.69)
	[H ,	A]

– в стационарном состоянии среднее значение от коммутатора оператора с гамильтонианом равно нулю. Тогда с учетом (2.67) среднее от производной оператора по времени равно нулю:

ˆ	(2.70)
dA / dt 0 .

Движение частицы является перемещением плотности вероятности и создает ток вероятности.

2.10. Ток вероятности

2.10. ТОК ВЕРОЯТНОСТИ

	Плотность вероятности w(r, t) \|		(r, t) \|2 в точке r изменяется с течением
времени.		Вероятность обнаружить	частицу	во всем пространстве
W	\|	(r, t) \|2 dV 1. Следовательно, вероятность перетекает из одного места
в другое. Вводится плотность тока вероятности j				j(r, t) и соответствующий

оператор, выражающийся через оператор скорости. Умножение на заряд час-

тицы e дает плотность электрического тока

je e j ,

вызванного движением

частицы.

Плотность тока вероятности определяется в виде

vˆ

pˆ

(2.71)

где pˆ

;

–

вектор

градиента, и учтено

Im C

C ) / 2i . Тогда

j jx nx

jy n y

jz nz ,

Re(

vˆx

)

Re(

pˆ x

)

(2.72)

Выражениям (2.71) и (2.72) ставим в соответствие операторы плотности тока вероятности, совпадающие с операторами скорости (2.67а) и (2.67б):

	ˆ	1	pˆ	i		ˆ
	j vˆ		pˆ		[H , r],
ˆ	vˆx	1	pˆ x		i	ˆ
jx	vˆx		pˆ x			H , x .	(2.72а)

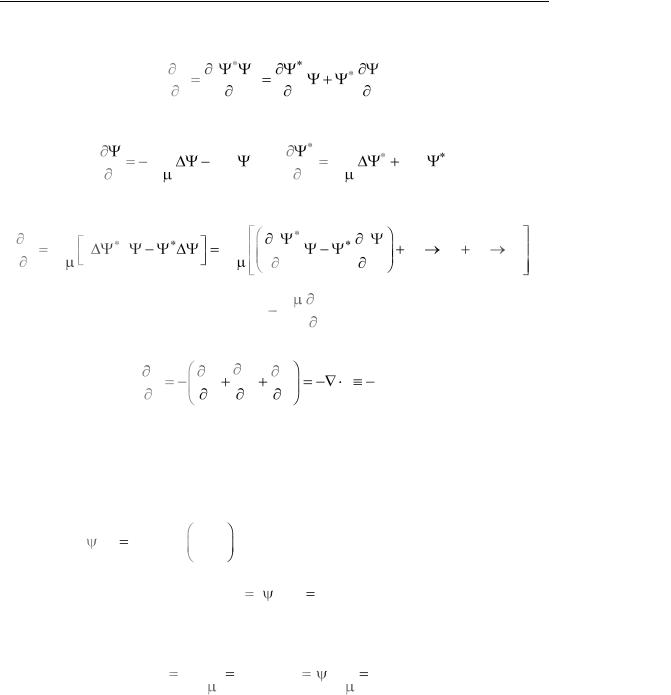
56 Глава 2. МАТЕМАТИЧЕСКИЙ АППАРАТ КВАНТОВОЙ МЕХАНИКИ

Уравнение непрерывности тока вероятности. Используем

w	(		)

t		t		t	t

и уравнение Шрѐдингера (2.54)

тогда

y) (x z) .

Первая круглая скобка справа равна

согласно (2.72), и аналогично

для остальных скобок. В результате получаем уравнение непрерывности

div j,

(2.73)

где div j – дивергенция плотности тока является потоком из единичного объ-

ема. Согласно (2.73) поток из объема уменьшает вероятность в этом объе-

ме. Следовательно, уравнение Шрѐдингера с эрмитовым гамильтонианом опи-

сывает систему, у которой нет источников и стоков частиц.

Ток вероятности для частицы с импульсом р. В состоянии пло-

ской волны	(r)	1	exp	i		(П.2.4) плотность вероятности
					p r
		h3/2			p r
					w(r)	\| (r) \|2	1

							h3
							h3

распределена равномерно по всему пространству. Из (2.72) находим

jx	1 px	wvx ,	2	p	w v .
			j \| \|
	h3

2.10. Ток вероятности

Плотность электрического заряда и тока для частицы с за-

рядом е:

e e w ,	je e j .
При равномерном движении заряда получаем известное соотношение
je	e v .

Из уравнения непрерывности (2.73) следует закон сохранения заряда в дифференциальной форме

	e	div je .
	t	div je .
	t

Плотность тока вероятности стационарного состояния.

Используем (2.63)

(r)

A(r) ei

(r) , где A и β – вещественные, тогда

w(r)

| (r) |2

A2 (r) .

Учитывая

A e i (ei

A iA ei

) A A iA2

из (2.71) получаем

. Используя j

v w, находим

w(r)

(r) ,

(r) .

(2.74)

Для стационарного состояния плотность тока вероятности пропорциональна плотности вероятности и градиенту фазы волновой функции. Если

фаза в разных точках одинаковая, то v			0 , j 0 . Из (2.74) получаем
div j	j	A (2 A	A ) 0 ,

где последнее равенство следует из (2.64). Следовательно, для стационарного состояния поток вероятности из любого объема равен нулю.

58	Глава 2. МАТЕМАТИЧЕСКИЙ АППАРАТ КВАНТОВОЙ МЕХАНИКИ
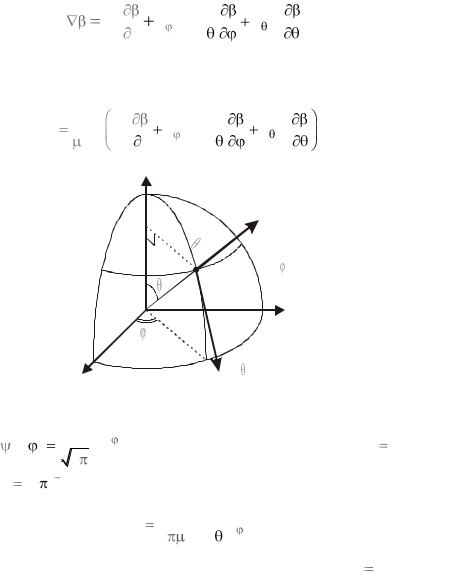
	В сферических координатах вектор градиента
	nr		n	1	n	1	.
		r		r sin
						r

Единичный орт ni направлен в сторону наибольшего возрастания аргумента, как показано на рис. 2.1. Из (2.74) находим

(2.75)

A nr

r sin

r s i n

Рис. 2.1. Единичные орты

Состоянию

( )

eim с проекцией момента импульса L

m соот-

ветствуют A2

(2 )

1 , β = mφ, тогда из (2.75) получаем

n ,

(2.75а)

r sin

следовательно,

ток вероятности вращается вокруг оси z. При m

0 вращение

отсутствует и ток равен нулю.

2.11. Матрица плотности

2.11. МАТРИЦА ПЛОТНОСТИ

Система в не полностью определенном состоянии не имеет волновой функции и описывается матрицей плотности, введенной в 1927 г. Львом Давидовичем Ландау (1908 1968) и независимо Джоном фон Нейманом (1903 1957).

Чистое и смешанное состояния. Чистое состояние описывается волновой функцией. Для смешанного состояния известна лишь вероятность Wi

того, что состояние описывается одной из возможных волновых функций i .

Между этими функциями не определены фазовые соотношения и отсутствует интерференция. Например, если величина, характеризующая систему, измерена не точно, то состояние смешанное и Wi является вероятностью i-го значения

величины. Так, если в атоме водорода положение протона не фиксировано, то электрон находится в смешанном состоянии. Если протон неподвижен или его движение упорядочено, то состояние электрона чистое. Чистое состояние разлагается по ортонормированному базису функций с коэффициентами, которые могут регулярно изменяться. Если коэффициенты изменяются беспорядочно, то состояние смешанное. Чистое состояние системы переходит в смешанное в процессе декогеренции, когда система взаимодействует с объектом, испытывающим хаотические изменения, например с макроскопическим телом. Декогеренция ускоряется с увеличением размеров квантовой системы. Система в чистом состоянии должна быть изолирована от окружающих тел и хаотически меняющихся полей посредством охлаждения, вакуумирования и экранирования. Уменьшение декогеренции необходимо для квантового компьютера и квантовой криптографии. Смешанное состояние описывается матрицей плотности, чистое состояние – как волновой функцией, так и матрицей плотности.

Матрица плотности чистого состояния. Функцию состояния

разлагаем по полному набору собственных функций { n} некоторого эрмито-

ва оператора ˆ :

(r, t)	cn (t) n (r)
	n

и описываем набором коэффициентов {cn (t)} . Для среднего значения величины a получаем

a	ˆ	*	Anm ,	(2.76)
	A dV	cm cn

n,m

Глава 2. МАТЕМАТИЧЕСКИЙ АППАРАТ КВАНТОВОЙ МЕХАНИКИ

где Anm

m dV

– матричный элемент оператора

A . Определяем мат-

рицу плотности

с элементами

cm cn* ,

(2.77)

тогда

mn Anm

Sp(

A) ,

(2.78)

n,m 1

где Sp(

Sp(A ) – шпур (от нем. die Spur – «след») – сумма диагональных

элементов матрицы;

| cn |2

является вероятностью обнаружения со-

стояния

в состоянии .

При N

2 получаем

2 ,

11 A11

22 A22

12 A21

21 A12

w1 a1

w2 a2

2 Re c1*c2 A12 ,

где A21

Ann

* ˆ

n dV

an ;

nn | cn

– вероятность ре-

(A12 ) ;

n A

зультата an . Наличие интерференционного слагаемого 2 Re c1*c2 A12 означает, что 1 и 2 в составе чистого состояния когерентные.

Матрица плотности смешанного состояния. Для смешанного

состояния коэффициенты разложения cn( j) зависят от не полностью опреде-

ленного параметра состояния j. Вместо (2.76) получаем

a	W	c( j)	c( j) *	A	,
		j m	n	nm
	j,m,n

где W j – вероятность j-го значения. Определяем матрицу плотности в виде среднего по значениям j:

____	J		c( j)	c( j) *
mn	W	j	c( j)	c( j) *	,	(2.79)
mn		j	m	n
	j 1

2.11. Матрица плотности

тогда (2.78) сохраняет форму

		N	____
		a	mn Anm Sp(		A) .
		a	mn Anm Sp(		A) .
		n,m 1
Диагональный элемент
		____ J		W j wm( j)
		mm		W j wm( j)
			j	1
дает вероятность состояния m ;			wm( j)	\| cm( j) \|2 является вероятностью состоя-
ния	m	в компоненте j смешанного состояния. Недиагональные элементы
	m

(2.79) характеризуют корреляцию состояний m и n. При J 2 , N 1 получаем

a W1 w1(1) A11 W2 w1(2) A11 .

Интерференционный член отсутствует, поэтому волновые функции компо-

нент c( j) (t)	m	и c( j ) (t)	m	смешанного состояния не когерентные.
m	m	m	m

Свойства матрицы плотности. Условие нормировки чистого со-

стояния
	Sp	1	(2.80)
получаем из (2.77):
Sp	mm	\| cm \|2	wm 1 .
m	m		m
Для смешанного состояния из (2.79) аналогично находим
	Sp	1.
	Sp	1.

Эрмитовость

(2.81)

следует из (2.77) и (2.79):

		*		*
		*	cncm	cmcn*	mn .
mn	nm		cncm	cmcn*	mn .

62 Глава 2. МАТЕМАТИЧЕСКИЙ АППАРАТ КВАНТОВОЙ МЕХАНИКИ

С учетом

a*	mn Anm	nm Amn a
	n,m	n,m

эрмитовость обеспечивает вещественность наблюдаемой величины.

Признак чистого состояния

2	(2.82)

получаем из (2.77) и (2.80):

( )ij	ik kj	cick ck c j cic j ck ck	ij Sp	ij .
k	k	k

При нарушении (2.82) состояние смешанное.

Изменение матрицы плотности со временем. Разложение вол-

новой функции по собственным функциям оператора с дискретным спектром

(r, t)	cn (t) n (r)
	n

подставляем в уравнение Шрѐдингера (2.54) и получаем

ˆ	i	cn n .
cn H n	i	cn n .
n		n

Умножаем уравнение на m , интегрируем по объему, учитываем ортонормированность функций и находим

		i cm	Hmn cn ,
			n
где Hmn	*	ˆ
где Hmn	m H n dV . Умножая результат на ck , получаем
		i ck cm	Hmn ck cn
			n
и комплексно сопряженное выражение
		i ck cm	Hnm ck cn .
			n

<<< < Предыдущая 1 2 3 4 56 / 366 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в папке Лекции Квант.мех. СГФ

#
11.03.20164.25 Mб2392014_krasnop.pdf
#
11.03.201613.88 Mб239Квант. мех..pdf
#
11.03.20164.98 Mб94Квант.лекция 0.doc
#
11.03.20169.91 Mб136Квант.лекция 1.doc
#
11.03.20161.84 Mб129Квант.лекция 2.doc
#
11.03.20165.14 Mб118Квант.лекция 3.doc
#
11.03.2016452.61 Кб89Квант.лекция 4-1.doc