Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Новосибирский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Лекции Квант.мех. СГФ / Квант. мех

..pdf

Скачиваний:

239

Добавлен:

11.03.2016

Размер:

13.88 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 365 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

2.6. Соотношение неопределенностей

тогда

ˆ ˆ

0 .

iB1

i A1 B1

B1A1

Для коммутатора

A1,

i C1

получаем

(2.31)

C1 .

Соотношение неопределенностей Гейзенберга. Полагаем

(2.32)

Используем

C ,

где учтено

i A1, B1

A, B

C .

Из (2.31) получаем

| c | .

(2.33)

Если операторы коммутируют, то c

0 ,

a b

0 и измерить обе величины

одновременно можно с неограниченной точностью.

Минимизация неопределенностей.

При

неопределенности

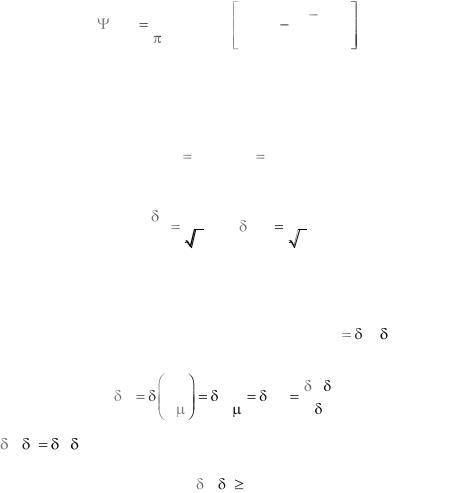
минимизированы в состоянии Ψ1, если соотношения (2.30) и (2.33) являются равенствами, откуда следует

ˆ	ˆ			\| c \|
A1	iB1 1	0 ,	b	2	a	.
				2	a

44 Глава 2. МАТЕМАТИЧЕСКИЙ АППАРАТ КВАНТОВОЙ МЕХАНИКИ

Подстановка (2.32) дает для

1 уравнение

| c |

2 ( a)2

i B

0 .

(2.34)

Когерентное состояние минимизирует неопределенности симмет-

рично

| c |1/2 /

2 ,

(2.35)

где a, b и c2 приведены к одинаковой размерности с помощью параметров системы. Когерентное состояние в наибольшей степени соответствует классическому объекту, его ввел Э. Шрѐдингер в 1926 г.

Сжатое состояние по а минимизирует неопределенности несимметрично в пользу величины а:

a b	1	\| c \|,	a	1	\| c \|1/2 .	(2.36)
	2
				2

Соотношение неопределенностей координата–импульс. Для

операторов проекции координаты и импульса выполняется xˆ, pˆ x				i , тогда
ˆ	, \| c \|	и из (2.33) находим
C	, \| c \|	и из (2.33) находим
		x px		(2.37)
		x px	2	(2.37)
			2

– чем точнее измеряется координата частицы, тем неопределеннее импульс, и наоборот. Следовательно, локализация частицы приводит к увеличению неопределенности ее импульса и кинетической энергии.

Волновой пакет. В (2.34) подставляем

| c |

A xˆ x ,

a x0

B pˆ x

b p0 ,

i dx

и получаем уравнение

x x0

1 0 .

d 2

2.6. Соотношение неопределенностей

Разделяя переменные, находим нормированное решение, называемое волно-

вой пакет

	1		i		(x x	)2
1(x)		exp		p0 x	0		.	(2.38)
1(x)	1/4d1/2	exp		p0 x	2d 2		.	(2.38)

В этом состоянии минимизированы модули неопределенностей координаты и импульса. Плотности вероятности в координатном и импульсном представлениях являются гауссовыми распределениями (см. пример 2.17) с центрами в точках

		x		x0 ,		p		p0 .
Безразмерные неопределенности
	x		1		,	p	d	1

	d
			2					2

минимизируют (2.37) симметрично, поэтому волновой пакет (2.38) является когерентным состоянием.

Соотношение неопределенностей энергия–время. Средняя

скорость частицы выражается через путь и время v x / t . Неопределенность кинетической энергии

E	p2	p	p	p v	p x	,
	2				t

тогда E t p x . Учитывая (2.37), находим

E t	.	(2.39)
	2

Возможные интерпретации:

•чем точнее измеряется энергия, тем больший промежуток времени необходим для этого;

•чем уже энергетический уровень возбужденного состояния, тем больше время его жизни.

46	Глава 2. МАТЕМАТИЧЕСКИЙ АППАРАТ КВАНТОВОЙ МЕХАНИКИ

2.7. УНИТАРНЫЙ ОПЕРАТОР. ОПЕРАТОРЫ ТРАНСЛЯЦИИ И ЭВОЛЮЦИИ

Среди операторов выделяется класс унитарных (от лат. unitas – единство), поворачивающих состояния физической системы в гильбертовом пространстве и сохраняющих их нормы и скалярные произведения. Такими операторами являются оператор трансляции – сдвига состояния в пространстве и оператор эволюции – перемещения состояния во времени.

			ˆ
Унитарный оператор U удовлетворяет условию
				ˆ ˆ	ˆ		ˆ		1.		(2.40)
			UU		U U				1.		(2.40)
Следовательно, эрмитово сопряжение дает обратный оператор
				ˆ	ˆ		1	.			(2.41)
				U	U			.			(2.41)
Оператор вида
				ˆ				ˆ
				ˆ	e	i f F			,		(2.42)
				U ( f )	e				,		(2.42)
ˆ	ˆ	f , удовлетворяет (2.41) и является унитарным
где F	F , f	f , удовлетворяет (2.41) и является унитарным
		ˆ		ˆ					ˆ	ˆ 1
		ˆ	e	i f F	e		i f F			ˆ 1	.
		U	e		e					U	.

Оператор

ˆ 1 dU (2.43)

i df f 0

называется генератором унитарного преобразования (2.42).

Свойства унитарного оператора

1. Унитарное преобразование функций

	i	ˆ	i ,		k	ˆ	k
		U				U

сохраняет их скалярное произведение и норму

i ,

k dV

ˆ ˆ

k dV

i ,

k .

2.7. Унитарный оператор. Операторы трансляции и эволюции			47
2. Унитарное преобразование оператора
ˆ	ˆ	ˆ ˆ
A	U	A U

и его собственных функций сохраняет собственные значения и коммутацион-

ные соотношения. Так, если		ˆ	a		, то
ные соотношения. Так, если		A	a		, то
ˆ	ˆ	ˆ ˆ	ˆ		ˆ ˆ			ˆ	a		.
A	U AU U				U A	aU			a		.
						ˆ			ˆ ˆ	является унитарным
3. Произведение унитарных операторов U									U1 U2	является унитарным
оператором
ˆ	ˆ ˆ		ˆ	ˆ	ˆ	1 ˆ	1	,	ˆ ˆ
U (U1U2 )			U2	U1	U2	U1		,	U U 1 .
			ˆ	преобразует волновую функцию
Оператор трансляции Ta				преобразует волновую функцию
		ˆ	(x, t)		(x	a, t) .					(2.44)
		Ta	(x, t)		(x	a, t) .					(2.44)

Это соответствует сдвигу системы по координате на расстояние a. Для полу-

чения явного вида оператора разлагаем

(x a, t) в ряд Тейлора и учитываем

pˆ x

, тогда

a, t)

(x, t)

(x, t) a2 2

(x, t)

...

pˆ x

...

(x, t) exp

a pˆ x

(x, t) ,

a pˆ x .

(2.45)

exp

Обобщаем (2.45) на случай перемещения на а:

a pˆ .

(2.45а)

exp

Согласно (2.42) оператор трансляции является унитарным.

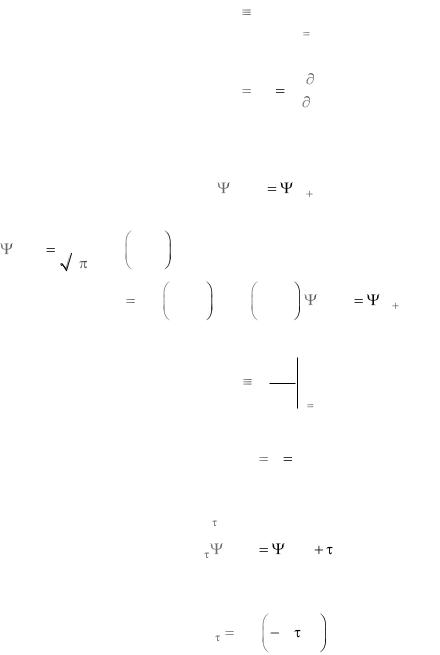
48	Глава 2. МАТЕМАТИЧЕСКИЙ АППАРАТ КВАНТОВОЙ МЕХАНИКИ

Генератор трансляции вдоль оси x

ˆ		ˆ
ˆ	dTa			.
Gx
Gx	i da
Подстановка (2.45) в (2.46) дает			a	0
			a	0

ˆ	pˆ x
Gx
Gx		i		x
		i		x

– генератор трансляции совпадает с оператором импульса.

Оператор сдвига импульса ˆ

(2.46)

(2.47)

ˆ	(x)	p p (x)
Tp p	(x)	p p (x)
1		1

приводит к изменению импульса частицы на p. Подставляя сюда состояние

p (x)

exp

(2.10) с импульсом p, получаем

p xˆ

, exp

p p (x) .

(2.48)

exp

p x

p (x)

Генератор преобразования

ˆ dTp Gp i dp

p 0

с учетом (2.48) имеет вид

ˆ	xˆ x
Gp

– генератор сдвига импульса совпадает с оператором координаты.

ˆ	преобразует волновую функцию
Оператор эволюции T
ˆ	(r, t) (r, t ) .	(2.49)
T

Это соответствует сдвигу системы во времени на τ. По аналогии с (2.45) записываем

ˆ	i	ˆ
T exp		H .	(2.50)

2.8. Уравнение Шрѐдингера

Знак «минус» в (2.50) обусловлен разными знаками пространственного и временного слагаемых в фазе волны де Бройля (1.11).

Генератор эволюции в (2.50)

		ˆ
ˆ	dT		.	(2.51)
H
H	i d
	i d		0
			0

Сравниваем (2.51) с генератором трансляции (2.46) и по аналогии с оператором импульса (2.47) получаем

(r, t)

(2.52)

(r, t)

Физический смысл

H находим, рассматривая его действие на волну де Бройля

E, p (x, t) c exp

( px

Et)

(1.11)

для частицы с полной энергией Е. Это

дает уравнение на собственную функцию

E, p (x, t) .

E, p (x, t)

– оператор полной энергии, или гамильтониан, является

Следовательно, H

генератором эволюции системы.

2.8. УРАВНЕНИЕ ШРЁДИНГЕРА

Волновая функция	системы, описываемой гамильтонианом	ˆ
		H ,

находится из уравнения, которое получил Э. Шрѐдингер в 1926 г. Функция

(r, t) удовлетворяет волновому уравнению Шрѐдингера. Если потен-

циальная энергия системы не зависит от времени, то полная энергия Е постоянна, зависимости волновой функции от координат и времени разделяются

E (r, t) E (r) fE (t) и E (r) находится из стационарного уравнения Шрѐдингера.

Правило сопоставления. При переходе от классической к квантовой теории физическим величинам ставятся в соответствие операторы. Если опе-

раторы эрмитовы, то соотношения между ними идентичны соотношениям

50	Глава 2. МАТЕМАТИЧЕСКИЙ АППАРАТ КВАНТОВОЙ МЕХАНИКИ

между их классическими аналогами. Если физической величине соответствует комбинация некоммутирующих операторов, то эрмитова форма получается посредством их симметризации. Правило сопоставления обеспечивает совпадение результатов квантовой и классической теорий при больших значениях квантовых чисел.

Оператор Гамильтона. Гамильтониан частицы в классической теории является суммой ее кинетической и потенциальной энергий, выраженных через координаты и импульсы:

H (p, r, t) 21 p2 U (r, t) .

Переход к операторам

rˆ r ,

pˆ

pˆ 2

2 ,

где

– оператор Лапласа, дает оператор Гамильтона

U (r,t) .

(2.53)

Волновое уравнение Шрѐдингера для

(r,t)

получаем из (2.52) и

(2.53):

U (r, t)

(2.54)

Стационарное уравнение Шрѐдингера. Если потенциальная

энергия не зависит от времени U U (r) , то полная энергия E сохраняется и

состояние стационарное. В (2.54) слагаемые с r и t разделены, решение ищем в виде

E (r, t)

E (r) fE (t) .

(2.55)

Подставляем (2.55) в (2.54), умножаем уравнение слева на

и находим

2.8. Уравнение Шрѐдингера

Левая и правая стороны зависят от разных переменных, поэтому они равны

постоянной

Е, как показано

далее.

Для

fE (t) находим

уравнение

dfE

E и решение

fE (t)

c exp

E t .

(2.56)

Для

E (r) получаем стационарное уравнение Шрѐдингера

U )

0 .

(2.57)

С учетом (2.53) оно является уравнением для собственной функции гамильтониана

ˆ	E E ,	(2.58)
H E

следовательно, Е – полная энергия. Для одномерной системы (2.57) получает вид

	d 2	2
	E			(E U )	E	0 .	(2.59)
	dx2		2	(E U )		0 .	(2.59)


Решение уравнения (2.59) дает волновую функцию							E (x) с полной энергией

Е и двумя свободными параметрами. Эти неизвестные находятся из граничных условий и из нормировки волновой функции.

Волновая функция стационарного состояния с энергией Е, сле-

дующая из (2.55) и (2.56):

E (r, t)	E (r) exp	i	E t ,	(2.60)
E (r, t)	E (r) exp		E t ,	(2.60)

периодически зависит от времени с частотой
	E / .			(2.61)

Суперпозиция состояний с дискретным спектром энергии

(r, t)	cn e	iEnt/	(r)	(2.62)
		E
		n

52 Глава 2. МАТЕМАТИЧЕСКИЙ АППАРАТ КВАНТОВОЙ МЕХАНИКИ

содержит коэффициенты cn , не зависящие от времени. Для их нахождения по-

лагаем t	0	, умножаем (2.62) на							E (r) , интегрируем по координатам, учи-
										m
тываем	*	E	d	3	r	E	,E	и после переобозначения m n находим
тываем	E	E	d		r	E	,E	и после переобозначения m n находим
		m	n			m		n
							c		*	(r) (r, 0) d 3r .
							n		En

Сравнивая (2.62) с (2.23) и учитывая (2.26), получаем вероятность обнаружения состояния с энергией En

			Wn	\| cn \|2 .
Стационарное состояние выражаем через вещественные функции
амплитуды A и фазы β
			(r)	A(r) ei	(r) .		(2.63)
Плотность вероятности w(r)		A2 (r) . Подставляя (2.63) в (2.57) и учитывая
			A ei		ei (	A iA	)
ei	A	A		i 2	A	A	,
находим
A A		2	(E U ) A i(2 A			A ) 0 .

		2

Разделяя действительную и мнимую части, получаем стационарное уравнение Шрѐдингера в виде системы

(2.64)

U )

0 .

(2.65)

Из (2.65) находим

V ) ,

(2.65а)

где

V (r)

учитывает

пространственную

быстроту

изменения ам-

плитуды.

<<< < Предыдущая 1 2 3 45 / 365 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в папке Лекции Квант.мех. СГФ

#
11.03.20164.25 Mб2392014_krasnop.pdf
#
11.03.201613.88 Mб239Квант. мех..pdf
#
11.03.20164.98 Mб94Квант.лекция 0.doc
#
11.03.20169.91 Mб136Квант.лекция 1.doc
#
11.03.20161.84 Mб129Квант.лекция 2.doc
#
11.03.20165.14 Mб118Квант.лекция 3.doc
#
11.03.2016452.61 Кб89Квант.лекция 4-1.doc