
Лекции Квант.мех. СГФ / Квант. мех
..pdf
1.5. Заряд в магнитном поле |
23 |
Квантование сопротивления. Для контура с током, плоскость которого перпендикулярна магнитному полю, используем баланс энергии. Приложенное к концам контура напряжение U поддерживает в цепи ток I и при переносе заряда q совершает работу | q | U . При увеличении магнитного потока
на |
возникает явление электромагнитной индукции и для поддержания то- |
||||||||||||||||
ка источник совершает работу |
I |
, |
тогда |
| q | U I |
. В цепи возникает |
||||||||||||
индуктивное сопротивление |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
R |
U |
|
|
. |
|
|
|
(1.35) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
I |
q |
|
|
|
|||||
Если ток переносится электронами |
| q | e , |
то кванту магнитного потока в |
|||||||||||||||
сверхпроводнике |
|
0 |
h / 2e соответствует квант сопротивления |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R0 |
|
|
|
h |
12, 906404 кОм . |
(1.36) |
|||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
2e2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Потоку (1.32) |
1 |
h / e |
с одноэлектронной проводимостью соответству- |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ет холловское сопротивление |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
RH |
|
h |
2R0 |
25,812807 кОм . |
(1.36а) |
|||||||||
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
e2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
При изменении магнитного потока на |
|
|
n |
1 |
по контуру переносится со- |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
гласно (1.35) заряд q |
|
|
/ RH |
n e . |
|
|
|
|
|
|
|
|
|||||
|
Квантование сопротивления баллистического проводника, в котором |
||||||||||||||||
электроны движутся без рассеяния: |
R |
R0 / N |
, где N |
1, 2,... – число акти- |
|||||||||||||
визированных поперечных мод движения, обосновал Рольф Ландауэр в 1970 г. [8]. Баллистическая проводимость наблюдается в графене и в многослойной углеродной нанотрубке. Сопротивление нанотрубки не зависит от ее диаметра и длины и равно кванту сопротивления, если длина трубки не превышает длину свободного пробега электрона в несколько микрометров. Углеродные на-
нотрубки допускают плотности тока до 1010 А/ см2 и пропускают ток без деградации в течение недель. Золото, серебро и медь выдерживают токи до
106 А/ см2 , далее они плавятся.
Квантование магнитного момента. Контур с током создает маг-
нитный момент, равный произведению силы тока на площадь контура и направленный перпендикулярно плоскости контура по правилу правого винта. Модули магнитного момента PM и момента импульса L заряда, создающего

24 |
Глава 1. ПОЛУКЛАССИЧЕСКАЯ КВАНТОВАЯ МЕХАНИКА |
|||
ток, |
взаимно пропорциональны PM gL L , где gL |
q |
– гиромагнитное |
|
|
||||
2 |
||||
|
|
|
||
отношение, известное из классической физики. Используя (1.27), получаем
модуль и проекцию орбитального магнитного момента электрона
P |
e |
n |
|
|
| m | , |
(P ) |
|
|
m , |
(1.37) |
|
|
B |
z |
B |
||||||
M |
2 |
|
|
|
M |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
где магнетон Бора |
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
0,58 10 4 эВ/ Тл |
|
|
(1.38) |
||
|
B |
2 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
ввел Вольфганг Паули в 1920 г. Следовательно, проекция орбитального маг-
нитного момента на направление поля пропорциональна магнитному квантовому числу m.
Рассмотренная полуклассическая теория не применима для системы с характерным размером, сравнимым с длиной волны де Бройля, когда отсутствует понятие траектории.
ПРИМЕРЫ 1
1.1. Электрон ускорен разностью потенциалов |
. Найти длину волны де |
Бройля. Для моноэнергетического коллимированного пучка электронов, падающих на кристалл с постоянной решетки d, получить условие максимальной интенсивности отраженной волны.
Электрон с нулевым начальным импульсом и полной энергией E 0 ускорен разностью потенциалов , как показано на рис. 1.5, а. На выходе по-
тенциальная энергия U |
e |
и длина волны де Бройля (1.13) |
|
|||||||
|
|
|
|
h |
1, 23 |
|
нм . |
(П.1.1) |
||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
2 e |
|
|
(B) |
|||
|
|
|
|
|
|
|
|
|
||
При |
1 B получаем рентгеновский диапазон |
|
1, 23 нм . |
|
||||||
|
На рис. 1.5, б волна де Бройля падает на кристалл под углом скольже- |
|||||||||
ния . Когерентные волны 1' и 2', отраженные от соседних кристаллических поверхностей, интерферируют с разностью хода
(AB) (BC) 2(AB) 2d sin .

Примеры 1 |
|
|
|
|
25 |
|
|
|
1 |
1 |
|
|
|
|
2 |
2 |
|
|
p |
d |
A |
C |
|
|
|
|
|||
|
|
|
|
B |
|
а |
|
|
|
б |
|
Рис. 1.5. Электронная пушка (а), отражение волны от кристалла (б) |
|
||||
Условие максимума интерференции (1.3) дает формулу Вульфа–Брэгга |
|
||||
2d sin |
n n , |
n |
1, 2,... |
(П.1.2) |
|
Если волны отражаются от поверхностей, находящихся на расстоянии |
md |
||||
друг от друга, где m 1, 2,... , |
то аналогично находим 2dm sin n M , |
где |
|||
Mmn – целое число, и формула (П.1.2) остается верной.
1.2.Для одномерной прямоугольной потенциальной ямы шириной a с абсолютно непроницаемыми стенками, показанной на рис. 1.6, а, получить допустимые значения энергии и импульса.
|
|
|
|
|
|
U(x) |
E |
|
|
U(x) |
|
|
E4 |
|
|
|
U(x) |
||||
|
|
|
E3 |
|
|
|
En |
|
|
|
|
|
|
|
|
|
E3 |
|
|
|
|
|
|
|
E2 |
|
|
|
|
|
|
|
Enкин(x) |
|
|
E2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
E1 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
U(x) |
|
|
|
|
|
|
||||
|
|
|
E1 |
|
|
|
|
|
|
|
xn |
|
|
x3 x |
|||||||
|
|
|
|
|
|
|
|
|
|
x3 0 |
|||||||||||
|
|
a/2 x |
|
|
|
|
|
||||||||||||||
a/2 |
0 |
0 |
x |
|
x |
||||||||||||||||
|
|
|
а |
|
|
|
|
|
б |
|
|
|
|
|
|
в |
|
|
|
|
|
Рис. 1.6. Потенциальные ямы
Частица с полной энергией En |
при | x | a / 2 имеет импульс |
||
|
|
|
|
pn |
|
2 En . |
|
Из условия квантования (1.17) с учетом, что движение совершается от a / 2 до a / 2 и обратно, находим
|
|
a/2 |
|
2 2 En |
dx h n , |
n 1, 2,..., |
|
|
|
a/2 |
|

26 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Глава 1. ПОЛУКЛАССИЧЕСКАЯ КВАНТОВАЯ МЕХАНИКА |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
E |
|
|
|
h2 |
n2 |
|
|
|
|
2 2 |
n2 , |
|
p |
|
|
|
|
h |
n . |
|
|
|
|
|
|
(П.1.3) |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
n |
|
|
8 a2 |
|
|
|
|
|
|
2 a2 |
|
|
|
|
|
n |
|
|
|
2a |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Для основного состояния n |
|
1 с минимальной энергией из (П.1.3) получаем |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
h2 |
|
|
|
|
2 2 |
, |
|
p |
|
|
|
|
h |
|
|
. |
|
|
|
|
|
|
|
(П.1.4) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
8 a2 |
|
|
|
2 a2 |
|
|
|
1 |
|
|
|
2a |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
1.3. |
Для треугольной потенциальной ямы U (x) |
f x, x |
|
0, показанной |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, x |
0, |
|
|
|
|
|
|
||
на рис. 1.6, б, получить допустимые значения энергии. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
Частица с полной энергией |
En |
движется между точками, |
|
в которых им- |
|||||||||||||||||||||||||||||||||||||||||||||||||
пульс |
и |
кинетическая энергия |
|
|
Eкин (x) |
|
E |
U (x) E |
f x |
|
обращаются в |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
||
нуль, т. е. в пределах от 0 до xn |
|
|
|
En / f . Учитывая |
pn (x) |
2 |
|
|
En |
f x , для |
|||||||||||||||||||||||||||||||||||||||||||
движения в прямом и обратном направлениях из (1.17) получаем |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
xn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
2 2 |
|
|
|
En |
|
|
f x dx 2 2 f |
|
|
xn |
|
|
|
x dx h n . |
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Интеграл вычисляется заменой |
|
x |
|
|
|
x y и равен |
2 |
|
|
E |
/ f |
3/2 , в результате |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
3 |
|
|
2/3 ( f )2/3 |
n2/3 . |
|
|
|
|
|
|
|
|
|
|
|
(П.1.5) |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
2 |
|
|
(2 |
)1/3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
1.4. Для |
гармонического |
|
|
осциллятора |
|
с |
потенциальной |
энергией |
|||||||||||||||||||||||||||||||||||||||||||||
U (x) |
kx2 / 2 , |
показанной |
на |
|
рис. |
1.6, в, получить |
допустимые |
значения |
|||||||||||||||||||||||||||||||||||||||||||||
энергии. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
На частицу действует |
упругая |
сила |
F |
|
|
dU / dx |
k x . |
|
Второй закон |
||||||||||||||||||||||||||||||||||||||||||||
|
x |
|
k x дает колебание x(t) |
|
x0 sin( t |
|
|
0 ) |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
Ньютона |
|
|
|
|
с частотой |
|
k / . |
||||||||||||||||||||||||||||||||||||||||||||||
Полная энергия и импульс |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
p2 |
|
kx2 |
|
p2 |
|
|
|
|
2 x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 2 x2 . |
|
|
|
|
||||||||||||||||||||||||
|
|
E |
|
|
n |
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
p (x) |
|
2 E |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
n |
2 |
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Примеры 1 |
27 |
Движение совершается между точками ( xn , xn ) , где импульс обращается в
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
нуль, |
тогда |
|
2En / . |
Условие |
|
квантования |
(1.17) в виде |
||||||
xn |
|
|
|
||||||||||
|
|
||||||||||||
|
xn |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
pn (x) dx |
h n после замены x |
xn sin |
дает |
|
||||||||
|
xn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
/2 |
|
|
|
|
|
|
|
|
|
|
|
|
cos2 |
|
2 n . |
|
|
|
|
|
|
|
2 2 E |
x |
d |
|
|||||
|
|
|
|
|
|
|
n |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
/2 |
|
|
|
Интеграл равен π/2, тогда |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
En n . |
|
|
(П.1.6) |
|
1.5. |
Щель с абсолютно отражающими стенками имеет протяженность |
|||||||||||
l |
10 2 м и ширину a |
1мкм . Электрон со скоростью v0 |
103 м/ с движется в |
||||||||||
плоскости щели и падает на нее по нормали. Во сколько раз увеличивается время прохождения расстояния l после установки щели? Как меняется направление движения электрона после прохождения щели с переменной протяженностью или с переменной шириной?
Модуль скорости электрона не изменяется при попадании в щель в силу закона сохранения энергии. Скорость внутри щели разлагаем на продольную
v и поперечную v |
составляющие, тогда v2 |
|
v2 v2 |
. Из (П.1.4) находим ми- |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
||
нимальное значение |
v |
|
p1 |
|
|
h |
|
364 м/ с , тогда |
|
|
|
|
|||||||
|
|
|
|
2 a |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1/2 |
|
|
|
|
|
|
v2 1/2 |
|
v0 |
|
|
|
|
|
|
h |
|
|
|
|
||||
v v2 |
|
|
, n |
|
1 |
|
|
|
1,073 . |
|
(П.1.7) |
||||||||
|
|
|
|
|
|
|
|
||||||||||||
0 |
|
|
|
|
|
n |
|
|
|
2 a v0 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
где n – показатель преломления волны де Бройля на щели. При v |
|
h |
из |
||||||||||||||||
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
2 a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(П.1.7) получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
h |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
. |
|
|
|
(П.1.8) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
2 |
|
2 a v0 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||

28 |
Глава 1. ПОЛУКЛАССИЧЕСКАЯ КВАНТОВАЯ МЕХАНИКА |
|
Для времени прохождения без щели t0 l / v0 |
и со щелью t l / v находим |
|
|
t / t0 v0 / v |
n . |
Относительное увеличение времени прохождения возрастает с уменьшением ширины щели, скорости и массы частицы.
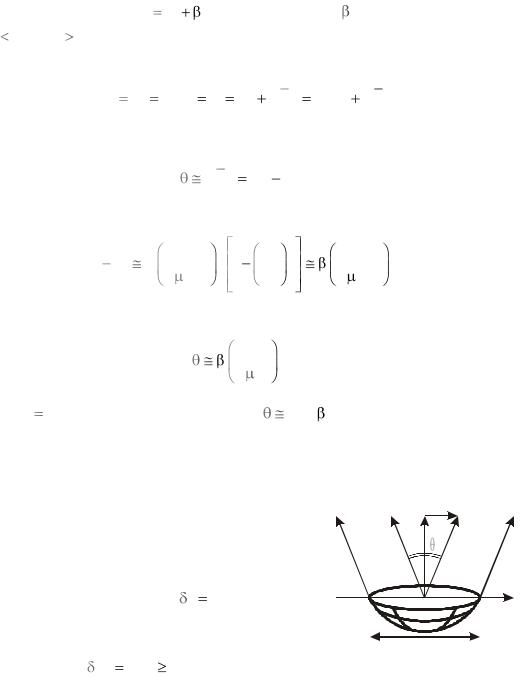
На рис. 1.7, а волна де Бройля проходит через щель шириной a и переменной протяженностью l1 l2 L с углом раствора 1. Пунктирные прямые
показывают волновые поверхности до и после щели. Между ними время распространения волны
t |
2 |
l2 |
n |
l2 |
t |
|
l1 |
|
|
x l1 |
n |
l1 |
|
x l2 |
L |
, |
|
|
|
|
|
|
|
|
|||||||||
|
v |
|
v0 |
1 |
|
v |
|
v0 |
|
v0 |
|
v0 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|||||||
тогда угол отклонения электрона щелью |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
x |
l2 |
(n |
. |
|
|
|
|
|||
|
|
|
|
|
|
|
L |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Результат совпадает с отклонением луча света тонкой призмой. Из (П.1.8) получаем
|
|
|
|
|
|
|
|
|
|
h |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0, 07 . |
|
|
(П.1.9) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
2 |
|
|
2 a v0 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
v0 |
v0 |
|
|
|
|
v0 |
v0 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
v1 |
a1 (a1<a2 ) a2 |
v2 |
|
|||||||||
|
|
v |
|
|
l2 |
v |
|
|
|
|
l |
|||||||
|
|
|
|
|
|
|
||||||||||||
|
|
|
l1 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
v0 |
|
|
|
v0 |
|
|
|
|
v0 |
|
|
v0 |
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
а |
|
|
|
|
|
|
|
б |
|
|
|
|
|
Рис. 1.7. Прохождение волны де Бройля через щель с переменной протяженностью (а), с переменной шириной (б)
Примеры 1 |
29 |
На рис. 1.7, б волна де Бройля проходит через щель протяженностью l и |
|
переменной шириной a2 a1 |
L с углом раствора 1. Из (П.1.7) получаем |
n2 n1 и v2 v1 . Пунктирные прямые показывают волновые поверхности до и |
|
после щели. Между ними время распространения волны
|
t |
l |
n |
l |
|
t |
|
|
|
l |
|
|
x l |
n |
l |
x l |
|
, |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
1 |
v |
|
1 v |
|
|
2 |
|
|
v |
|
|
|
v |
|
2 v |
v |
|
|
|
|
||||||||||
|
|
1 |
|
0 |
|
|
|
2 |
|
|
|
|
0 |
|
|
|
0 |
|
|
0 |
|
|
|
|
|||||||
тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x l |
|
|
(n |
n ) |
l |
. |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
1 |
|
|
2 |
|
L |
|
|
|
|
|
|
|
|
|
|
||
Из (П.1.8) получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n1 |
n2 |
|
1 |
|
|
h |
|
|
2 |
1 |
|
a1 |
2 |
|
|
|
|
|
h |
|
|
2 L |
, |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
2 2 a v0 |
|
|
a2 |
|
|
|
2 a v0 |
|
|
a |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
тогда угол отклонения электрона щелью |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
2 l |
. |
|
|
|
|
|
|
|
|
|
|
(П.1.10) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
2 v0 |
|
|
a3 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Для v0 105 м/ с |
из (П.1.10) |
находим |
|
|
|
0,13 . |
|
Подбором профиля щели |
|||||||||||||||||||||||
можно управлять волной де Бройля. Эксперимент с невидимостью двумерного объекта, использующий щель между линзой и плоскостью, см. в Physical Review Letters, 102, 213901 (2009).
1.6. Оценить угловую ширину диаграммы |
|
|
py |
||
направленности круглой антенны диаметром D, |
|
px |
|||
показанной на рис. 1.8, излучающей волну дли- |
|
||||
|
|
|
|
||
ной λ. |
|
|
|
|
|
Испущенный антенной фотон имеет неоп- |
|
|
|
|
|
ределенность координаты |
y D . Неопреде- |
|
|
|
y |
|
|
|
|||
|
|
|
|
|
|
ленность импульса в поперечном направлении |
|
|
|
|
|
находим из (1.9): |
|
|
|
|
|
|
|
D |
|||
|
|
|
|||
py 2 py |
h / D . |
Рис. 1.8. Излучение антенны |
|||
|
|
||||

30 |
Глава 1. ПОЛУКЛАССИЧЕСКАЯ КВАНТОВАЯ МЕХАНИКА |
|||||
Учитывая импульс фотона (1.7) |
px h / |
, получаем угловую ширину пучка |
||||
|
|
2 py |
|
|
. |
(П.1.11) |
|
|
px |
|
D |
||
Чем больше диаметр антенны, тем меньше угловая ширина диаграммы направленности.
1.7. Оценить неустранимую погрешность, возникающую при двукратном измерении координаты свободной частицы массой μ, если измерения проводятся с интервалом времени t. Найти оптимальную погрешность.
Если при t 0 измеряется координата частицы с погрешностью x(0) , то согласно (1.9) возникает неопределенность скорости
|
p |
|
h |
|
v |
|
|
|
. |
|
x(0) |
|||
С учетом движения частицы повторное измерение через время t дает погрешность
|
|
|
|
h |
|
x(t) |
x(0) |
v t |
x(0) |
|
t . |
x(0) |
|||||
Погрешность второго измерения тем больше, чем меньше погрешность первого измерения. Минимизируем действие измерителя на объект условием
|
|
|
d x(t) |
0 |
, 1 |
|
|
|
|
|
h |
t |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
d x(0) |
[ |
|
|
2 |
||||||||
|
|
|
|
|
|
|
x(0)] |
|
|
|
|
||||
и находим стандартный квантовый предел погрешности координаты |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x(0) |
|
|
h t |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(П.1.12) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x(t) |
2 x(0). |
|
|
|
|
|||||
Для атома углерода массой (C) |
19, 9 10 27 кг и размером 10 4 мкм нахо- |
||||||||||||||
|
|
|
|
|
|
||||||||||
дим x(0) 180 t(c) (мкм) . Для электрона |
x(0) |
|
270 t(c) (мкм) . Погреш- |
||||||||||||
ность уменьшается, если частица прикреплена к массивному телу.
При измерении импульса погрешность первого измерения не влияет на второе измерение, поскольку импульс свободного объекта сохраняется в промежутке между воздействиями.

 Г л а в а 2
Г л а в а 2
МАТЕМАТИЧЕСКИЙ АППАРАТ КВАНТОВОЙ МЕХАНИКИ
Для выхода за рамки применимости полуклассической теории используется математический аппарат операторов в гильбертовом простран-
стве. Физической величине ставится в соответствие оператор. Набор его собственных значений дает возможные результаты измерения величины. Для его собственных функций определена операция скалярного произведения, и они образуют ортонормированный базис в гильбертовом пространстве. Частица описывается волновой функцией. Она получается в результате решения уравнения Шрѐдингера. Разложение волновой функции по ортонормированному базису того или иного оператора дает вероятности возможных результатов измерений.
2.1. ВОЛНОВАЯ ФУНКЦИЯ
Состояние частицы описывает комплексная функция (пси), являющаяся амплитудой вероятности обнаружения частицы. Совокупность ее аргументов соответствует так называемому представлению. В координатном представ-
лении
(r, t) ,

32 |
Глава 2. МАТЕМАТИЧЕСКИЙ АППАРАТ КВАНТОВОЙ МЕХАНИКИ |
|
в |
импульсном представлении |
(p, t) . Детектор частиц регистрирует |
| |2 . Величина |
|
|
|
dW (r, t) | |
(r, t) |2 dV w(r, t) dV |
является вероятностью обнаружения частицы в момент t в объеме dV около точки r ;
w(r, t) | (r, t) |2
– плотность вероятности, т. е. вероятность обнаружения частицы в единичном объеме около точки r . Условие нормировки
| (r, t) |2 dV 1
означает, что частица всегда обнаруживается при обследовании всего пространства. Функция состояния:
1) определена с точностью до постоянного фазового множителя; состоя-
ния |
и ei , где |
const , физически неразличимы; |
||
2) |
квадратично интегрируема, т. е. |
| |
|2dV существует; |
|
3) |
удовлетворяет принципу суперпозиции – если возможны состояния |
|||
1 и |
2 , то возможно состояние |
|
|
|
|
|
a1 |
1 |
a2 2 , |
где a1, a2 – комплексные числа.
Рассмотрим операторы, которые преобразуют волновую функцию.
2.2. ОПЕРАТОРЫ
Физической величине ставится в соответствие оператор. Исключением яв-
ляется время, которое считается параметром. Оператор ˆ есть правило, по ко-
A
торому из функции , находящейся правее оператора, получается функция Φ:
ˆ
A .
Явный вид оператора зависит от представления. Рассмотрим примеры операторов в координатном представлении.
