
Лекции Квант.мех. СГФ / Квант. мех
..pdf
7.2. Квантовая частица и электромагнитное поле |
253 |
||
|
|
|
|
С учетом [ , A] div A оператор |
ˆ |
коммутирует с векторным потенциалом в |
|
P |
|||
радиационной калибровке (7.5).
Действие магнитного поля на квантовую систему учитывается подста-
новкой импульса |
|
|
|
pˆ |
|
q A , |
(7.13) |
|
i |
|
|
когда заменяется оператор кинетического импульса pˆ |
в формулах, описы- |
||
вающих систему без магнитного поля. Электрическое поле со скалярным потенциалом υ учитывается слагаемым потенциальной энергии
U U0 q υ . |
(7.14) |
В результате уравнение Шрѐдингера и операторы физических величин содержат потенциалы A, .
Калибровочное преобразование. Фаза волновой функции частицы
неизмерима, поскольку физические характеристики являются билинейными комбинациями волновой функции. Измерима только разность фаз волновой функции в разных точках. Поэтому изменение фазы, называемое калибровоч-
ным преобразованием:
(r, t) |
(r, t) |
eiβ |
(r, t) , |
|
(r, t) |
[ (r, t)] |
e iβ |
(r, t) , |
(7.15) |
не должно влиять на физические характеристики системы.
Если сдвиг фазы не зависит от координат и времени, то (7.15) называется глобальным преобразованием. Оно не изменяет уравнение Шрѐдингера и
физические характеристики. |
|
|
При локальном преобразовании |
r, t нарушается уравнение Шрѐ- |
|
дингера. Инвариантность уравнения достигается введением |
компенси- |
|
рующего поля, описываемого потенциалами A(r, t) и (r, t) , |
с которыми |
|
взаимодействует частица. Мера взаимодействия характеризуется электриче-
ским зарядом частицы q. В результате локальное изменение фазы волновой функции эквивалентно появлению электромагнитного поля, которое вво-
дится подстановками (7.13) и (7.14). Если преобразование (7.15) сопровожда-

254 Глава 7. ЗАРЯЖЕННАЯ ЧАСТИЦА В ЭЛЕКТРОМАГНИТНОМ ПОЛЕ
ется градиентным преобразованием потенциалов (7.4) с калибровочной функцией f ( / q) в виде
A A A |
|
, υ υ υ |
|
|
, |
(7.16) |
|
|
|
||||
|
q |
|
q |
t |
|
|
то уравнение Шрѐдингера и выражения для физических характеристик сохра-
няют свои формы. Действительно, они содержат |
ˆ n |
с n |
0,1, 2 . При калиб- |
||||||||||||||
p |
|||||||||||||||||
ровочном преобразовании из (7.13) – (7.16) получаем |
|
|
|
|
|||||||||||||
pˆ |
pˆ |
|
|
|
q A |
ei |
|
ei |
|
q A |
|
ei pˆ , |
|||||
|
|
|
|
|
i |
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
pˆ 2 |
(pˆ )2 |
|
ei pˆ 2 |
, |
|
|
|
|
|||
|
i |
|
|
U |
|
i |
|
|
U |
|
|
ei |
ei |
i |
|
U |
. |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
t |
|
|
t |
|
|
t |
|
|
t |
|
|
|||
В результате плотность вероятности, плотность тока вероятности и урав-
нение Шрѐдингера
|
|
1 |
|
|
ˆ |
2 |
|
|
|
w |
, j |
Re ( *pˆ |
) , |
p |
|
U |
i |
|
|
|
|
|
|
||||||
|
|
μ |
|
|
2μ |
|
t |
||
не изменяются при калибровочном преобразовании. Не изменяются и соб-
ственные значения оператора любой физической величины. Производные фазы волновой функции частицы с зарядом q сопоставили с электромагнитными потенциалами Герман Вейль и Фриц Лондон в 1923–1928 гг.
|
Калибровочное преобразование (7.15), где |
|
|
f q , является унитарным |
||||||||||
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
i |
ˆ |
|
|
|
|
|
|
|
|
|
ˆ |
|
|
|
|
f Q |
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
q , где |
|||
преобразованием с оператором (2.42) в виде U ( f ) e |
|
, если Q |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
ˆ |
|
ˆ |
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
dU |
|
|
|
|
|
|
|
|
|
||||
Q |
– оператор заряда. Из (2.43) |
Q |
|
|
|
|
получаем, |
что генератором |
||||||
|
||||||||||||||
|
|
|
i df |
|
f |
0 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||||
калибровочного преобразования является оператор заряда. Для частицы с электрическим зарядом калибровочная инвариантность обеспечивается
7.2. Квантовая частица и электромагнитное поле |
255 |
|
|
взаимодействием с электромагнитным полем и его переносчиком – фотоном. Обобщение калибровочного преобразования на другие виды сохраняющихся зарядов – изоспин, лептонное число, барионное число – предложили Чжэньнин Янг и Роберт Миллс в 1954 г. На этой основе построены теории электрослабого и сильного взаимодействий, для которых компенсирующими полями и переносчиками взаимодействия являются частицы бозоны со спином 1: фотон;
W , W , Z 0 ; восемь глюонов (от англ. glue – клей).
Операторы физических величин. С учетом подстановок (7.13) и
(7.14) гамильтониан, уравнение Шрѐдингера, плотность тока вероятности
(2.71) и плотность электрического тока в электромагнитном поле получают вид
|
|
ˆ |
|
|
|
|
pˆ |
2 |
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
U , |
(7.17) |
||||
|
|
H |
|
|
|
2μ |
U |
|
|
2μ |
i |
q A |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
q A |
U |
|
|
|
|
i |
|
|
, |
(7.18) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
2μ |
i |
|
|
|
|
|
|
|
t |
|||||||||||||||
j |
1 |
Re ( |
*pˆ |
) |
|
Im( * |
) |
|
q |
A | |
|2 , |
||||||||||||||||
|
|
|
|||||||||||||||||||||||||
|
μ |
|
|
|
|
|
|
|
|
|
|
|
|
μ |
|
|
|
|
|
|
|
μ |
|
||||
|
|
ˆ |
|
1 |
pˆ |
1 |
|
|
|
|
|
i |
|
ˆ |
|
||||||||||||
|
|
j |
|
|
μ |
|
μ |
|
i |
q A |
|
|
[H ,r] , |
(7.19) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ |
|
|
|
|
|
|
|
||
|
|
|
|
|
je |
|
q j |
|
|
Re |
|
|
H |
|
|
. |
|
|
(7.20) |
||||||||
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Плотность тока вероятности (7.19) калибровочно инвариантна и удовлетворяет уравнению непрерывности (2.73).
Используя (7.13) и (7.2), находим
pˆ x , pˆ y |
i q Bz , |
pˆ y , pˆ z |
i q Bx , |
pˆ z , pˆ x i q By . |
(7.21) |
Операторы проекций кинетического импульса заряда в магнитном поле не коммутируют.

256 |
|
|
|
|
|
|
Глава 7. ЗАРЯЖЕННАЯ ЧАСТИЦА В ЭЛЕКТРОМАГНИТНОМ ПОЛЕ |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ |
|
|
pˆ x |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ |
|
|
H |
|
|
|
|
|
|
|
|||||
Используя (7.17), уравнение Гамильтона x |
vˆx |
|
pˆ x |
|
|
μ |
и (2.33), полу- |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
чаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
vˆ |
x |
, vˆ |
y |
|
i q B |
, |
vˆ |
y |
, vˆ |
z |
i q B |
, |
vˆ |
z |
, vˆ |
x |
|
|
i q B |
y |
, |
||||||||||||
|
|
|
|
μ2 |
z |
|
|
|
μ2 |
x |
|
|
|
|
|
μ2 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
δv |
|
|
δv |
|
q |
B |
|
, |
δv |
|
δv |
|
q |
B |
|
, |
δv |
|
δv |
|
|
|
q |
B |
|
|
. |
(7.22) |
|||||
x |
y |
|
z |
y |
z |
|
x |
x |
z |
|
|
|
y |
||||||||||||||||||||
|
|
|
|
2μ2 |
|
|
|
|
2μ2 |
|
|
|
|
2μ2 |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Проекции скорости заряда в магнитном поле определяются одновременно с ограниченной точностью.
Для стационарного состояния с определенной энергией |
E (r, t) ψ(r) e iEt |
|||||||||||||
используем (2.63) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
eiβ(r) |
|
|
||||
|
ψ(r) |
|
w(r) |
|
|
|||||||||
и выражаем плотность тока вероятности (7.19) и скорость v |
j / w через фазу |
|||||||||||||
β(r) и плотность вероятности w(r) |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
q |
, |
|
||||
j |
|
|
w(r) |
|
β(r) |
|
|
|
A |
|
||||
|
μ |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
q |
|
|
||||
|
v |
|
|
|
|
β(r) |
|
A . |
|
(7.23) |
||||
|
|
|
μ |
|
|
|||||||||
Результат обобщает (2.74) на случай магнитного поля.
7.3. УРОВНИ ЛАНДАУ
Состояния заряда в стационарном однородном магнитном поле получил Лев Давидович Ландау в 1930 г.
Гамильтониан заряда q в магнитном поле согласно (7.17)
ˆ |
1 |
ˆ |
|
2 |
. |
H |
2μ |
(P |
qA) |
|
7.3. Уровни Ландау |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
257 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
В декартовых координатах для поля B |
|
(0, 0, B) используем калибровку |
||||||||||||||||||||||||||||||||
(7.10) A (0, Bx, 0) , тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
ˆ |
1 |
|
|
ˆ |
2 |
|
|
ˆ |
|
|
|
|
|
|
|
|
|
2 |
|
ˆ 2 |
|
|||||||
|
|
|
|
|
H |
|
|
2μ |
|
|
Px |
(Py |
|
|
qB x) |
|
|
Pz . |
(7.24) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Уравнение Шрѐдингера |
|
ˆ |
|
|
Eψ получает вид |
|||||||||||||||||||||||||||||
Hψ |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
2 |
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
iqB |
2 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
ψ |
|
|
|
|
|
|
|
2μ |
|
|
x2 |
|
|
|
|
z2 |
|
|
|
y |
|
|
|
|
|||||||||||||
|
|
2 |
2 |
|
|
2 |
|
|
|
|
|
2 |
|
|
|
qB |
|
|
|
|
|
qB |
2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2i |
|
|
|
|
x |
|
|
|
|
|
|
|
x |
ψ Eψ . |
||||||||
|
|
2μ |
x2 |
y2 |
|
|
z2 |
|
|
|
y |
|
|
|
||||||||||||||||||||
ˆ |
|
ˆ |
коммутируют с |
ˆ |
|
, поэтому решение содержит произве- |
||||||||||||||||||||||||||||
Операторы Py |
и Pz |
H |
||||||||||||||||||||||||||||||||
дение собственных функций операторов |
|
ˆ |
|
ˆ |
|
|
|
|
|
|||||||||||||||||||||||||
Py и Pz |
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
i |
|
||||||
|
|
|
ψ(x, y, z) υ(x) exp |
|
|
|
py y |
exp |
|
pz z . |
||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||
Движение по оси z не ограничено, |
pz |
– любое вещественное число, |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
E |
|
|
1 |
|
p2 . |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
2μ |
|
z |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Подставляем решение в уравнение, делим его слева на ψ и получаем уравнение для υ(x)
υ |
2μ |
E |
|
(ω |
|
x) |
2 |
μ |
ω |
|
x p |
|
p2y |
υ υ |
2μ |
[E |
U (x)]υ 0 |
, |
|
M |
c |
|
|
c |
y |
|
|
||||||||||
|
2 |
|
|
|
|
2 |
|
|
2μ |
|
2 |
M |
1 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
qB |
|
|
μω2 |
(x x )2 |
|
где |
ω |
|
– циклотронная частота (1.23); |
U (x) |
c |
– эффектив- |
|
|
|
||||||
|
c |
μ |
|
1 |
2 |
1 |
|
|
|
|
|
|
|
ная потенциальная энергия. Сравниваем с уравнением гармонического осцил-
258 Глава 7. ЗАРЯЖЕННАЯ ЧАСТИЦА В ЭЛЕКТРОМАГНИТНОМ ПОЛЕ
лятора (3.23), который колеблется с частотой ω и амплитудой нулевых колеба-
|
|
|
|
|
|
|
|
ний (3.40) x0 |
/ (μω) относительно точки x |
0 : |
|||||
|
|
ψ |
2μ |
E |
μω2 |
x2 |
ψ 0 . |
|
|
2 |
2 |
||||
|
|
|
|
|
|
||
Решаемая задача соответствует осциллятору, колеблющемуся относительно точки
x1 |
py |
|
(7.25) |
||
qB |
|||||
|
|
|
|||
|
|
|
|||
с частотой ωc и с амплитудой (3.40) нулевых колебаний x0 |
/ (μωc ) |
||||

 / (qB) lM , совпадающей с магнитной длиной (1.30). Используя (3.32), находим решение уравнения
/ (qB) lM , совпадающей с магнитной длиной (1.30). Используя (3.32), находим решение уравнения
|
1 |
|
|
|
|
x |
x |
|
|
(x |
x )2 |
|
|
||||
υn (x) |
|
|
|
|
|
Hn |
|
1 |
|
exp |
|
|
1 |
|
, |
|
|
|
|
|
|
|
lM |
|
|
|
|
2lM2 |
|
||||||
|
π1/2 2n n!lM |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
где n 0, 1, 2,... и x1 – квантовые числа состояния. |
|
|
|
|
|
|
|||||||||||
Уровни энергии Ландау. Энергия |
движения |
заряда в |
плоскости |
||||||||||||||
(x, y) квантуется аналогично гармоническому осциллятору (3.39) |
|
||||||||||||||||
E |
ω n |
1 |
|
|
e |
n |
1 |
|
|
B μ |
|
(2n |
1) B , |
|
(7.26) |
||
|
|
|
|
|
|
|
B |
|
|||||||||
M ,n |
|
c |
2 |
|
|
μ |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где учтено (1.38). Уровни энергии показаны на рис. 7.1, а. При |
n 1/ 2 из |
||||||||||||||||
(7.26) следует полуклассическое приближение (1.28). С учетом поступательного движения по оси z получаем
E |
ω n |
1 |
|
pz2 |
μ |
B |
(2n 1) B |
pz2 |
. |
(7.27) |
|
|
|
||||||||
n |
c |
2 |
|
2μ |
|
|
2μ |
|
||
|
|
|
|
|
|
|
||||
В (7.27) не учтено взаимодействие спинового магнитного момента заряда с магнитным полем. Случайный потенциал, действующий на электрон, приводит к конечной ширине уровней Ландау EM ,n .

7.3. Уровни Ландау |
259 |
|
|
Соотношение неопределенностей для координат. При большой
длине волны де Бройля λ r отсутствует понятие траектории заряда. Координатам центра циклотронного движения (7.25) с учетом (7.13) ставим в соответствие операторы
xˆ1 |
1 |
|
pˆ y |
1 |
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
x , |
ˆ |
y , |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
qB |
Py |
|
qB x |
|
iqB |
y |
|
y1 |
|||||||||||||
|
qB |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[xˆ1, yˆ1] |
1 |
|
ˆ |
|
|
|
|
|
|
|
|
|
|
. |
(7.28) |
|||||||
|
|
qB |
|
Py |
, y |
|
|
i qB |
|
|
|
i μωc |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Используя (2.33) и (1.30), получаем соотношение неопределенностей |
||||||||||||||||||||||||
|
|
|
|
δx δy |
|
|
|
|
|
|
1 |
l |
2 |
. |
|
(7.29) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|||||||
|
|
|
|
1 1 |
2μω |
c |
2qB |
2 |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Координаты центра циклотронного движения определяются одновременно с ограниченной точностью. Из (7.29) с учетом (1.33) следует неопреде-
ленность магнитного потока
δ |
B δx δy |
|
|
1 |
. |
(7.30) |
|
|
|
||||||
|
|
||||||
|
1 |
1 |
2q |
|
4π |
|
|
|
|
|
|
|
|||
Магнитный поток измеряется при помощи заряда с точностью, не превышающей величины кванта магнитного потока.
Число состояний на уровне Ландау. Состояние υn (x) зависит от
положения центра циклотронного движения x1 , энергия (7.26) не зависит от x1 , поэтому уровень Ландау вырожден. Для движения, ограниченного обла-
|
L |
L |
|
Ly |
|
Ly |
|
L |
|
L |
|
|||
стью |
x |
x |
x |
и |
|
|
y |
|
, условие |
x |
x |
x |
|
с учетом (7.25) ог- |
|
|
|
|
|
||||||||||
|
2 |
|
2 |
|
2 |
|
2 |
|
2 |
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
раничивает импульс |
qBLx / 2 |
py qBLx / 2 |
интервалом |
py qBLx . Про- |
||||||||||
странственное ограничение по оси y вызывает квантование |
p y . Из граничного |
|||||||||||||
условия Борна–Кармана (3.8) получаем
|
i |
|
i |
||
exp |
|
py ( y Ly ) |
exp |
|
py y , |
|
|
||||

260 Глава 7. ЗАРЯЖЕННАЯ ЧАСТИЦА В ЭЛЕКТРОМАГНИТНОМ ПОЛЕ
py Ly 2π N h N , py |
h |
N , |
|
||
|
Ly |
|
где N – целое число. Допустимые значения импульса имеют шаг δpy h / Ly .
Учитывая степень вырождения σ состояний по спину и (1.32) |
1 |
h / q , нахо- |
||||||
|
|
|
|
|
|
|
|
|
дим кратность вырождения уровня n |
|
|
|
|
|
|
||
gn |
py |
σ |
qB Lx Ly |
σ |
|
σ . |
|
(7.31) |
|
|
|
|
|||||
|
δpy |
h |
|
1 |
|
|
|
|
Число состояний на уровне Ландау пропорционально числу квантов магнитного потока, приходящихся на область, доступную для движения заряда.
На основании (7.29) полагаем, что циклотронное движение занимает площадь
δS |
2π l2 |
h |
. |
|
(7.32) |
|||
|
||||||||
1 |
M |
qB |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
На площадке Lx Ly находится число движений |
N |
Lx Ly |
|
|
, совпадающее с |
|||
δS1 |
1 |
|||||||
|
|
|
|
|
||||
кратностью вырождения уровня без учета спина. Следовательно, каждое цик-
лотронное движение захватывает квант потока |
1 . Число состояний на |
|||||||||||||||
единице площади, т. е. поверхностная плотность состояний: |
|
|||||||||||||||
|
|
n |
1 |
|
qB |
|
|
B |
. |
|
|
|
(7.33) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
B |
δS1 |
|
h |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
1 |
|
|
|
|
|
|
||||||
Уровни Ландау в импульсном пространстве следуют из (7.27) |
||||||||||||||||
E |
1 |
2μ ω n |
1 |
|
|
p2 |
1 |
|
|
p2 |
p2 |
p2 |
, |
|||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||||||
n |
2μ |
c |
2 |
|
|
z |
|
|
2μ |
x |
y |
z |
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||||
где pz изменяется непрерывно. Модуль импульса в плоскости, перпендикулярной полю, удовлетворяет соотношению Онсагера
p2 |
p2 |
p2 |
2 eB n |
1 |
, |
n 0, 1, 2,... |
(7.34) |
|
|||||||
n |
x |
y n |
|
2 |
|
|
|
7.4. Эффект Ааронова–Бома |
|
|
|
|
|
261 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
pz |
n = 0 |
|||
|
h c |
|
|
|
|
|||||||
|
|
|
|
|
|
|||||||
|
n = 2 |
|
|
|
|
|
|
n = 1 |
||||
|
|
|
|
|
|
|||||||
5/2 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
n = 2 |
||||
3/2 |
|
n = 1 |
|
|
|
|
|
|
|
py |
||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||
1/2 |
|
n = 0 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||
|
px |
|
|
|
|
|
|
|||||
0 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
а |
|
|
|
|
|
б |
|||
Рис. 7.1. Уровни Ландау
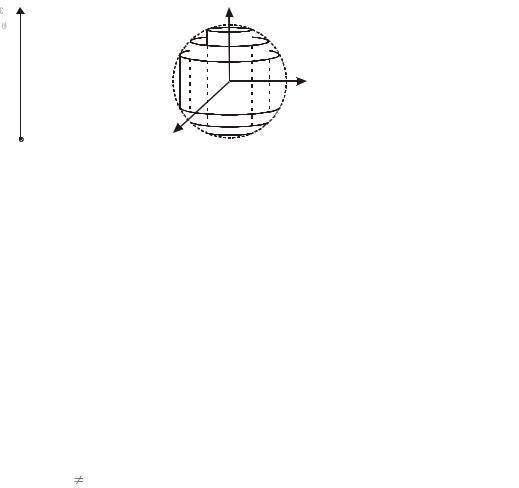
В p-пространстве поверхности с энергиями En имеют вид коаксиальных
цилиндров, показанных на рис. 7.1, б. При низкой температуре энергия системы зарядов ограничена энергией Ферми, что соответствует сфере в p- пространстве. С увеличением магнитного поля радиусы цилиндров увеличиваются, внешний цилиндр выходит за пределы поверхности Ферми и опустошается от зарядов. Это вызывает колебания электропроводности – эффект Шубникова–де Гааза и колебания магнитной восприимчивости – эффект де Гааза–ван Альфена.
7.4.ЭФФЕКТ ААРОНОВА–БОМА
Вклассической электродинамике заряд, находящийся в области, где E и
B равны нулю, но (υ, A) 0 , не подвергается силовому действию поля, т. е. векторный потенциал A(r) , не зависящий от времени, и скалярный потенциал υ(t) , не зависящий от координат, не действуют на классический заряд. Дэвид Бом и Якир Ааронов показали в 1959 г., что фаза волновой функции заряда
изменяется под действием скалярного и векторного потенциалов даже в том случае, когда нет силового действия поля на частицу. Магнитный эф-
фект Ааронова–Бома подтвержден интерференционными экспериментами
R.G. Chambers в 1960 г., A. Tonomura в 1982 |
г., электрический эффект – |
G. Matteucci и G. Pozzi в 1985 г. Влияние полей E |
и B , не равных нулю лишь |
вне области, которая доступна для частицы, на состояние квантовой частицы свидетельствует о нелокальности квантового состояния. Рассмотрим эф-
фект Ааронова–Бома в магнитном и электрическом полях.
262 |
Глава 7. ЗАРЯЖЕННАЯ ЧАСТИЦА В ЭЛЕКТРОМАГНИТНОМ ПОЛЕ |
Магнитный эффект. Пусть в рамках полуклассической квантовой механики заряд q движется перпендикулярно магнитному полю В по замкнутой траектории. Полуклассическое квантование (1.22) с учетом (1.32) дает
т |
ж |
n |
ц |
, |
(7.35) |
|
p Чdl = h зn + |
ч |
|||||
|
||||||
(n) |
и |
1 |
ш |
|
|
|
|
|
|
|
|
где 1 = h / q ; n – магнитный поток через поверхность, ограниченную траекторией n =1, 2, 3,... Согласно (1.17) и (3.55) изменение фазы при прохождении частицей траектории n без магнитного поля
υn = |
1 |
т p Чdl . |
|
||
|
|
(n) |
Из (1.34) и (7.35) следует вклад магнитного поля в изменение фазы при движении по замкнутой траектории
|
υM = 2π |
|
n |
= |
| q | |
|
n . |
|
(7.36) |
|||||
|
|
|
|
|
|
|
||||||||
|
|
1 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для незамкнутой траектории |
между |
точками r0 и r поток |
обобщается: |
|||||||||||
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
= т |
A Чdl ® т A Чdl , тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
(L) |
r0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
υM = |
2π r |
A Чdl = |
| q | |
r |
|
Чdl . |
|
||||||
|
|
т |
|
|
|
т |
A |
(7.37) |
||||||
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
||||||||
|
|
1 r |
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
Влияние векторного потенциала на фазу волновой функции является эффектом Ааронова–Бома. Рассмотрим действие поля соленоида на плоский ротатор на основе уравнения Шрѐдингера.
Ротатор в поле соленоида. Силовые линии бесконечно тонкого и длинного соленоида, показанного на рис. 7.2, сосредоточены внутри соленоида и рассеиваются на бесконечности. Вне соленоида B = 0 и отсутствует силовое действие поля на заряд, находящийся вне соленоида.
В цилиндрических координатах
Bz (r) 2π δ(r2 ) ,
