Файловый архив студентов. Файловый архив студентов.
1296 вузов, 5031 предметов.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Новосибирский государственный технический университет
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:

Лекции Квант.мех. СГФ / Квант. мех

..pdf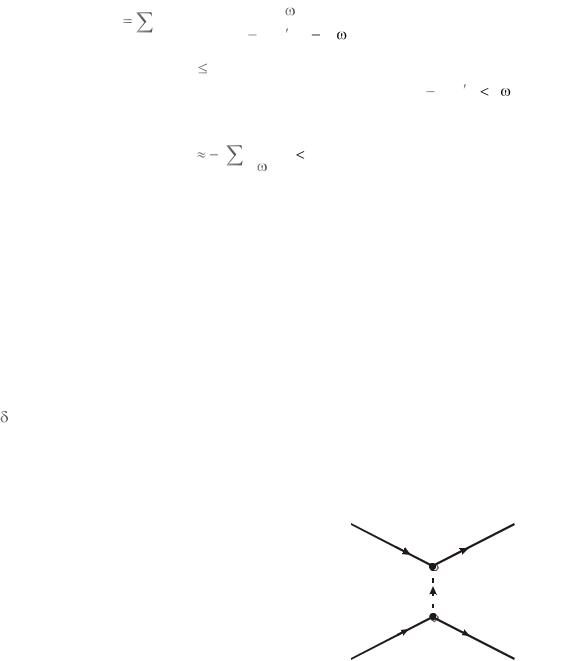
Скачиваний:
239
Добавлен:
11.03.2016
Размер:
13.88 Mб
Скачать
☆
Рис. 6.3. Взаимодействие между электронами 1 и 2

Примеры 7

223

| Vp,q |2

 

2

 

 

.

 

 

 

 

[E(p ) E(p )]2

(

)2

q

 

1

1

 

 

 

При низких температурах T

30 К электроны активированы в тонком слое

около поверхности Ферми и изменение их энергии мало | E(p1) E(p1) | , тогда

 

| Vp,q |2

Uвз 2

 

 

0 .

 

 

q

(q)

Следовательно, при низких температурах взаимодействие между электронами в кристалле имеет характер притяжения. В результате образуется коррелированно движущаяся куперовская пара электронов. Ее возникновение объясняется тем, что при рассеянии на неоднородностях кристаллической решетки электрон испускает фонон, что соответствует колебанию узлов решетки – положительных ионов. Притягиваясь к электрону, они проскакивают по инерции положения равновесия и образуют область повышенной плотности положительного заряда, которая притягивает другой электрон. Разрыв куперовской пары требует затраты энергии, которая является энергетической щелью в спектре возбуждений. Эффект, открытый Леоном Купером в 1956 г., служит основой теории сверхпроводимости Бардина–Купера–Шриффера. Как показывает теория, расстояние между взаимодействующими электронами r 2 мкм, что превышает среднее расстояние между электронами про-

водимости или ионами решетки в 104 раз.

7.6. Кулоновское взаимодействие зарядов в полупроводнике и сила Ампера, действующая на электроны в катушке электродвигателя со стороны электронов магнита, убывают обратно пропорционально квадрату расстояния

и объясняются в квантовой электродинамике

 

p

p'

обменом виртуальными фотонами. Показать, что

 

такой фотон является пространственно-подоб-

2

2

2

 

 

 

 

 

ным, т. е. его модуль импульса, умноженный на

 

B

q

скорость света, превышает энергию и сила ука-

 

 

занных взаимодействий передается между элек-

 

A

 

тронами мгновенно, на каком бы расстоянии они

1

p

 

ни находились.

p'

Диаграмма рис. 6.3 описывает рассеяние элек-

 

1

1

 

 

 

тронов 1 и 2 посредством обмена виртуальным фотоном в низшем порядке теории возмущений.

224 Глава 6. ПРИБЛИЖЕННЫЕ МЕТОДЫ

Сила взаимодействия между электронами пропорциональна числу обменов. Плотность фотонов, испускаемых электроном, убывает обратно пропорционально квадрату расстояния. Эта зависимость определяет число обменов и силу взаимодействия между электронами. На рис. 6.3 величины являются 4-векторами импульса. Для фотона q (q, Eq ) , где q – импульс, Eq – энергия.

В вершинах A и B выполняются законы сохранения энергии и импульса

A: E1

E1

Eq ,

p1

p1

q ;

B: E2

E2

Eq ,

p2

p2

q .

Уравнения в каждой строке возводим в квадрат и взаимно вычитаем, предварительно умножив уравнение для импульсов на квадрат скорости света С. Для реальных частиц учитываем

E2

C2 p2

C4 2 ,

i

1, 2 ,

 

i

i

 

 

 

 

 

 

 

и получаем

 

 

 

 

 

 

 

 

C 2q2

E2

2E E

q

2C 2p q ,

 

q

1

 

1

 

 

C 2q2

E2

2E E

q

2C 2p

2

q ,

 

q

2

 

 

 

 

откуда

 

 

 

 

 

 

 

 

E E C 2p q E E C 2p

2

q .

1 q

1

 

2

q

 

 

 

В системе отсчета центра масс p2

p1 находим

 

 

 

 

E 0 ,

q 0 ,

q2

 

E2

C 2q2 0 .

q

 

 

 

q

 

 

 

 

Энергия виртуального фотона равна нулю, он переносит импульс и силовое воздействие, 4-вектор импульса пространственно-подобный. В реляти-

вистской динамике энергия объекта и модули его скорости и импульса связаны соотношением

V C2 p / E .

 

Для пространственно-подобного фотона с E 0 получаем V

. Фотон

испускается одним электроном и поглощается другим электроном в один и тот же момент, сила взаимодействия передается мгновенно. Полученный

6.2. Стационарное возмущение вырожденных состояний

225

вывод подтвержден экспериментально для электромагнитного поля в ближней зоне магнитного диполя с переменным током, см.: Journal of Applied Physics. 101, 023532 (2007); Письма в ЭЧАЯ. Т. 6, № 4. С. 519–527 (2009). Фотоны радиационного поля являются реальными, переносят импульс и энергию

E

C p в вакууме со скоростью света V C и имеют

0 , q2 0 . Ограни-

чение скорости V C относится к частицам с времяподобным 4-импульсом

q2

E2 C2q2 C4 2 0 .

 

6.2. СТАЦИОНАРНОЕ ВОЗМУЩЕНИЕ ВЫРОЖДЕННЫХ СОСТОЯНИЙ

Для вырожденных состояний E(0)

E(0)

и теория разд. 6.1 неприменима

 

 

 

 

 

 

n

 

k

 

 

 

 

 

из-за обращения в нуль знаменателей в (6.13), (6.15) и (6.16).

 

 

 

Рассмотрим двукратно вырожденные состояния

(0) и

(0)

, удовлетво-

 

 

 

 

 

 

 

 

 

 

 

1

2

 

 

ряющие уравнению Шрѐдингера

 

 

 

 

 

 

 

 

 

 

 

ˆ

(0)

 

(0)

(0)

 

 

(0)

(0)

(0)

 

 

 

 

 

H0 k

E

 

k

,

E

 

E1

E2 .

 

 

 

Уравнению также удовлетворяет суперпозиция

 

 

 

 

 

 

 

 

(0)

 

(0)

 

 

(0) .

 

 

 

 

 

 

 

 

 

 

 

1

 

 

2

 

 

 

 

Появившееся возмущение действует на

(0)

с коэффициентами

1 и

1 ина-

1

че, чем на

(0)

с коэффициентами

 

и

2 . Состояния получают разные

2

2

энергии, и вырождение снимается. При произвольных коэффициентах

и

система переводится в состояние с неопределенной энергией. Первый порядок теории возмущений дает и , с которыми состояние сохраняет опре-

деленность энергии, а также величину возмущенной энергии. Если возмущение обладает некоторой симметрией, то она переносится на искомую суперпозицию состояний.

Невозмущенные состояния

(0)

и

(0)

ортонормированны:

 

 

 

 

1

 

2

 

 

(0) *

(0)

dV

k ,l ,

 

(k, l

1, 2) .

(6.18)

k

l

 

226 Глава 6. ПРИБЛИЖЕННЫЕ МЕТОДЫ

Вводим суперпозиции

(0)

(0)

(0)

,

n 1, 2 .

(6.19)

n

n 1

n 2

Найдем коэффициенты в (6.19) из условия, что возмущение в первом порядке

не перемешивает

(0) и

(0) .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Условие ортонормированности

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(0) *

 

(0)

dV

 

 

 

 

 

(6.20)

 

 

 

 

 

 

 

 

 

 

 

n

 

 

k

 

 

n,k

 

 

 

связывает коэффициенты

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

*

 

 

*

 

1 1,

 

 

 

 

 

*

,

 

 

*

(6.21)

 

 

 

 

1

1

 

1

 

 

 

2

 

1

 

2

1 .

Решения выражаем через вещественные параметры

и γ:

 

 

 

 

 

 

 

1

cos

 

ei

,

 

 

1

sin

e i

,

 

(6.22)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ei

 

 

 

 

 

 

 

e i .

 

 

 

 

 

 

2

 

 

 

sin

,

 

 

2

cos

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Если известны

1

и

1

для

1(0) , то из (6.22) получаем коэффициенты ортого-

нального состояния

(0) .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Возмущенные состояния. Повторяем рассуждения разд. 6.1 приме-

нительно к состояниям

(0)n , которые не перемешиваются возмущением в пер-

вом порядке. Тогда

(1)

 

 

(1)

 

0 ,

pnk

 

0 и из (6.9) получаем

 

1

 

 

2

 

 

 

 

 

 

 

 

 

 

ˆ

 

E

(1)

(0)

 

0

, (n

1, 2) .

 

(6.23)

 

 

 

 

 

 

V

 

 

 

n

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Подставляем (6.19) для n

 

1 в (6.23)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ˆ

 

E

(1)

 

 

 

 

(0)

 

 

(0)

 

0 .

 

(6.24)

 

 

 

 

 

V

 

 

 

 

1

1

 

1

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Ищем коэффициенты

1 ,

 

1

и поправку к энергии E(1) . Проектируем уравне-

ние на орт

(0)

,

умножая (6.24)

слева на

 

(0)

*

и интегрируя по объему.

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

Аналогично проектируем (6.24) на орт

 

 

(0)2 . Учитывая (6.18), получаем

 

 

 

 

 

 

 

 

V

 

 

 

E(1)

 

 

1

V

1

0,

 

 

 

 

 

 

 

 

 

 

11

 

 

 

 

 

 

12

 

 

 

(6.25)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

E(1)

 

 

 

 

 

 

 

 

 

 

 

V

 

1

 

V

 

 

 

1

0,

 

 

 

 

 

 

 

 

 

 

21

 

22

 

 

 

 

 

 

 

 

6.2. Стационарное возмущение вырожденных состояний

 

227

где Vik

(0) *

ˆ

(0)

 

 

 

 

 

(1)

 

i

V

k dV . Для нахождения E

 

используем условие раз-

решимости системы уравнений (6.25)

 

 

 

 

 

V11

 

V12

 

2

(V11

V22 )

(V11V22

V12V21) 0 .

 

 

 

 

V21

 

V22

 

 

Учитывая

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

V12 V21 V12 V12

|V12 |2 ,

 

находим энергии состояний после снятия вырождения:

 

 

E

E(0)

1

,

 

E

E(0)

 

2

,

 

 

 

 

 

 

1

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

E1,2(1)

 

1

(V11

V22 )

 

1

(V11

V22 )2

| V12 |2 .

 

(6.26)

1,2

2

4

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Подстановка E(1)

1,2

в (6.25) дает

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1,2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

V12

 

,

 

2

 

 

V12

.

 

 

 

 

(6.27)

 

 

1

1

V11

2

 

2

V11

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Из (6.27) с учетом нормировки |

k |2

 

| k |2 1

получаем коэффициенты со-

стояния (6.19), которое не перемешивается возмущением.

 

 

 

 

Симметричное возмущение по отношению к

(0) и

(0)

удовле-

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

2

 

творяет условиям

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

V11

V22 ,

 

V12

V21 .

 

 

 

 

 

 

Из (6.26) и (6.27) находим

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1,2 V11 V12 ,

 

1

 

 

 

1 ,

 

2

 

2 ,

 

 

 

 

тогда (6.19) получает вид

 

(0)

1

 

1

1

 

 

 

2

 

 

 

 

 

(0)

1

 

2

2

 

 

 

2

 

 

 

 

(0)(0)

12

(0)(0)

1 2

,

. (6.28)

228 Глава 6. ПРИБЛИЖЕННЫЕ МЕТОДЫ

Из (6.26) находим

E E(0)

(V

V ),

E

E(0) (V

V ),

 

1

11

12

2

11

12

(6.29)

 

 

 

 

 

 

 

E1

E2

2

V12 ,

 

 

Возмущение линейно отодвигает уровни друг от друга. Для невырожден-

ных состояний отталкивание уровней возникает во втором порядке теории возмущений.

Пример симметричного возмущения. Однородное электрическое

поле E действует на плоский ротатор в плоскости его вращения, как показано

ˆ

pE cos , где θ – угол между полем и дипольным мо-

на рис. 6.1. Тогда V

ментом ротатора. Из примера 6.1 используем

E(0)

2 / 2J

z

m2

,

(0)

( ) (2 ) 1/2 e i m

,

m 0, 1, 2,...

m

 

 

 

m

 

 

 

Для вырожденных при m

 

0 состояний получаем

 

 

pE

V11 V22 2

2

cos d 0 ,

0

pE

V21 V12 2

2

1

 

 

cos e i2m d

pE (

2m,1 2m, 1) 0 .

2

0

 

 

 

 

 

В первом порядке теории возмущений уровни энергии не изменяются. Из (6.28) находим состояния, которые не перемешиваются возмущением:

(

)

1

(0)

(0)

1

 

 

 

cos(m ) ,

 

 

 

 

 

|m|

|m|

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(

)

1

(0)

(0)

1

 

 

 

sin(m ) .

 

 

 

 

 

|m|

|m|

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Возмущение четное, поэтому оно сохраняет состояния с определенной четно-

 

 

(0)

стью

, но перемешивает

|m| .

6.3. Зависящее от времени возмущение

229

6.3. ЗАВИСЯЩЕЕ ОТ ВРЕМЕНИ ВОЗМУЩЕНИЕ

Возмущение

ˆ

действует при t 0 на стационарную невырожден-

V (r, t)

ную систему с дискретным спектром. В первом порядке теории возмущений энергетические уровни не изменяются, но возникают переходы системы между уровнями. Получим вероятности переходов.

Невозмущенные состояния cтационарной системы с дискретным спектром

(0)

(r, t) exp

i

E t

 

(r)

 

 

 

k

 

k

k

 

удовлетворяют уравнениям

 

(0)

 

 

 

 

 

 

 

 

 

 

 

i

k

 

ˆ

(0)

 

ˆ

 

 

 

 

 

 

 

 

 

H0

k

,

H0 k (r)

Ek k (r) ,

 

 

 

t

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ортонормированны

 

 

 

 

 

 

 

 

 

 

 

 

 

 

*

dV

n,k ,

 

(0)

* (0)

dV

 

 

 

 

 

n k

 

n

k

n,k

 

 

 

и образуют полный базис

 

(0)k (r, t)

. Стационарная суперпозиция состояний

(0) (r, t)

c(0)

(0) (r, t)

c(0) exp

 

i

E t

 

(r)

(6.30)

 

 

k

 

k

 

k

k

 

k

k

 

k

 

 

 

 

 

 

 

 

 

 

 

 

 

 

имеет неопределенную энергию и удовлетворяет уравнению Шрѐдингера

 

 

(0)

ˆ

(0)

 

ˆ

 

 

 

 

 

 

 

i

 

 

 

 

 

 

 

 

 

 

t

 

H0

 

,

H0

k (r)

Ek

k (r) .

 

 

(6.31)

 

 

 

 

 

 

 

 

 

 

 

 

 

Вероятность обнаружения системы на уровне k :

Wk | ck(0) |2 ,

(6.32)

где ck(0) – амплитуда вероятности. При отсутствии возмущения вероятность

Wk не зависит от времени, т. е. спонтанные переходы отсутствуют.

230

 

 

 

 

 

 

Глава 6. ПРИБЛИЖЕННЫЕ МЕТОДЫ

Возмущенное состояние

 

(r, t)

удовлетворяет уравнению

 

 

 

 

i

 

 

ˆ

ˆ

 

 

 

 

 

(6.33)

 

 

 

 

 

(H0

V )

 

 

 

 

 

 

 

 

 

 

t

 

 

 

 

 

 

 

и разлагается по базису

 

(0)k (r, t)

 

 

 

 

 

 

 

 

 

(r, t)

c

(t)

(0) (r, t)

c (t) exp

i

E

t

 

(r)

(6.34)

 

k

k

k

 

k

 

k

k

 

k

 

 

 

 

 

 

 

 

 

 

 

 

 

 

с зависящими от времени коэффициентами ck (t) . Для их нахождения подстав-

ляем (6.34) в (6.33) и учитываем (6.31)

i

 

dck

 

i

 

i

ˆ

 

 

exp

 

Ek t k (r)

ck exp

 

Ek t

V

k (r) .

k

dt

 

 

 

 

 

 

 

k

 

 

 

 

Снимаем суммирование в левой части уравнения, проектируя его на (0)n (r,t) .

Для этого умножаем уравнение слева на exp

i

E t

* (r)

и интегрируем по

 

 

 

 

 

 

 

 

 

 

 

 

 

n

n

 

объему. С учетом

n

k dV

 

n,k

получаем уравнение для коэффициентов

 

 

 

i

dcn

 

 

 

c ei

nk t V

 

,

 

(6.35)

 

 

 

 

 

 

 

 

 

 

 

 

 

dt

 

 

k

 

nk

 

 

 

 

 

 

 

 

 

k

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

где Vnk (t)

* ˆ

 

k dV

– матричный элемент возмущения;

n V (r, t)

 

 

 

 

 

 

 

1

(E

E )

 

 

 

(6.36)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

nk

 

n

k

 

 

 

 

– боровская частота перехода с уровня k на уровень n. Из (6.35) следует, что быстрота изменения амплитуды вероятности обнаружения системы на уровне n определяется переходами со всех уровней k на уровень n. Найдем cn (t) , ис-

пользуя теорию возмущений.

Первый порядок теории возмущений. Коэффициент ищем в виде

c (t)

c(0)

c(1)

(t) ,

(6.37)

n

n

n

 

 

6.3. Зависящее от времени возмущение

231

где cn(0) – коэффициент невозмущенного разложения (6.30); cn(1) (t) – поправка,

вызванная возмущением. Подставляем (6.37) в (6.35) и ограничиваемся первым порядком возмущения

 

 

dc(1)

 

c(0)ei

nk t V

 

 

 

 

i

 

n

 

 

 

(t) .

 

 

 

 

 

 

 

 

 

 

 

 

 

dt

 

k

nk

 

 

 

 

 

 

k

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Интегрируя по t в пределах (0, t) , получаем

 

 

 

 

 

 

 

i

 

t

 

 

 

 

c(1)

(t)

 

 

 

c(0) ei

nk t V

(t ) dt .

(6.38)

 

 

 

 

 

 

 

 

 

 

 

 

n

 

 

 

k

k

nk

 

 

 

 

 

 

 

0

 

 

 

 

Учтено, что возмущение начинает действовать при t

0 и c(1) (0)

0 .

 

 

 

 

 

 

 

 

 

 

 

n

 

Переход между состояниями. Пусть при t

0 система находилась в

состоянии m, тогда c(0)

k,m

и (6.37) дает

 

 

 

k

 

 

 

 

 

 

 

 

 

 

 

 

 

cn (t)

 

n,m

cnm (t) ,

 

 

 

где cnm (t) – амплитуда вероятности перехода m

n в момент t. Из (6.38)

получаем

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

i

t

 

 

 

 

c

(t)

 

ei nm t V (t ) dt .

 

(6.39)

 

 

 

nm

 

 

 

 

 

 

 

nm

 

 

 

 

 

 

 

 

 

 

0

 

 

 

 

Правый индекс m соответствует начальному состоянию, левый – конечному. Состояние системы в момент t находим из (6.34):

(r, t)

 

(r) exp

 

i

E

 

t

 

c (t) exp

 

i

E

t

 

(r) .

m

 

 

m

 

 

n

 

 

 

 

 

 

 

 

 

nm

 

 

 

n

 

 

 

 

 

 

 

 

 

 

 

 

 

n

 

 

 

 

 

 

 

 

Вероятность перехода m

 

 

n ,

 

т. е. вероятность обнаружения систе-

мы в состоянии n, если при t

0 было состояние m

n , находим из (6.39):

 

 

 

 

 

 

 

 

 

1

 

t

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

W

 

(t)

| c

 

(t) |2

 

 

 

ei nmt V (t ) dt

 

.

 

(6.40)

 

 

 

 

 

 

 

nm

 

nm

 

 

 

 

2

 

nm

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0

 

 

 

 

 

 

 

 

232

Глава 6. ПРИБЛИЖЕННЫЕ МЕТОДЫ

Состояние при t . По истечении большого промежутка времени интегрирование в (6.39) проводим в бесконечных пределах:

 

 

 

 

i

 

 

i

nmt

 

 

 

 

 

 

 

 

2 i

 

 

) .

 

 

c ( )

 

 

e

 

 

V (t) dt

 

 

 

V (

 

 

 

 

nm

 

 

 

 

 

 

 

nm

 

 

 

 

 

nm

nm

 

Амплитуда перехода m

 

n при

 

t

 

 

пропорциональна фурье-образу

возмущения на частоте перехода

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

i

nmt

 

 

(t) dt .

 

 

 

 

 

V

(

nm

)

 

 

 

 

 

 

e

 

 

V

 

 

 

 

 

nm

 

 

2

 

 

 

 

 

 

 

nm

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Частные случаи:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

а) постоянное возмущение Vnm

 

 

const

дает

 

 

 

 

V

(

 

) V (

 

 

) V

 

1

(E E )

V (E E ) ,

 

 

 

 

 

 

 

nm

 

nm

nm

nm

 

 

nm

 

 

 

 

n

 

m

 

nm

 

n m

 

 

 

Wnm (t) 4 2 |Vnm |2 (En

Em ) .

 

 

Выполняется закон сохранения энергии, переходы происходят между вырожденными состояниями;

б) адиабатическое

возмущение

соответствует матричному элементу

Vnm (t) , слабо изменяющемуся за время

1 /

0 , тогда по теореме о частотной

полосе V

(

) – мало при

0

и существенны переходы с низкими часто-

nm

 

 

 

 

 

 

 

тами nm

 

0 .

 

 

 

 

 

 

 

Периодическое возмущение с частотой

, действующее при t 0 :

 

 

 

ˆ

 

 

ˆ

 

 

 

 

 

 

V (r, t)

A(r)H (t) cos t

 

приводит к амплитуде перехода (6.39) в виде

 

 

 

 

 

 

i

 

t

 

 

 

 

 

c

(t)

A

ei nmt

cos

t dt ,

 

 

 

 

 

nm

nm

 

 

 

 

 

 

 

 

 

0

 

 

 
Соседние файлы в папке Лекции Квант.мех. СГФ
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности