Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Новосибирский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Лекции Квант.мех. СГФ / Квант. мех

..pdf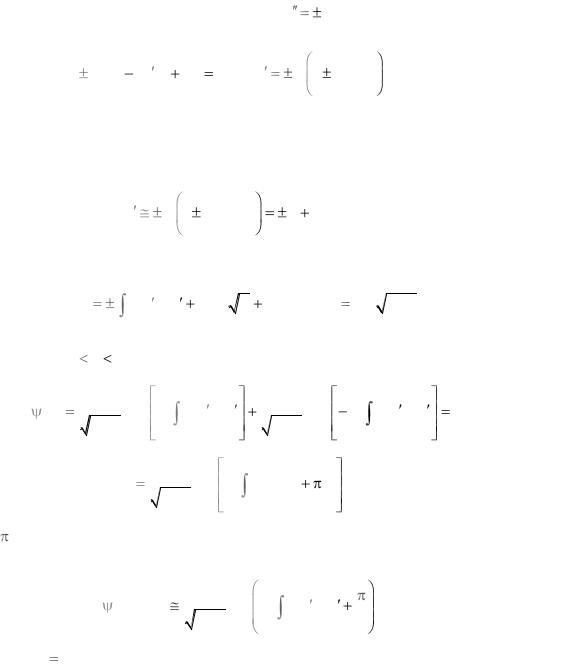

Скачиваний:

241

Добавлен:

11.03.2016

Размер:

13.88 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 3613 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

3.5. Квазиклассическое квантование ВКБ

123

Второе приближение. Подставляем S

в (3.53) и получаем

(S )2

0 ,

i dp

1/2 .

Учитываем (3.56)

1 , разлагаем скобку в ряд и оставляем первые два

слагаемых

p 1

i dp

2 p2 dx

2 p dx

тогда

S(x)

p(x ) dx i ln p c ,

S2 (x) i ln p(x) .

Из (3.52) для x1

x2 получаем общее решение

(x)

exp

p(x ) dx

exp

p(x ) dx

p(x)

(3.58)

sin

p(x) dx

p(x)

где C – фаза,

набираемая волной в точке поворота x1. Сравнивая (3.58) с

асимптотикой решения для линейного потенциала (П.3.26)

(x x )

sin

1 x

p(x ) dx

p(x)

находим C 1/ 4 . Если потенциальная энергия имеет особенность в точке поворота, то полученный результат неприменим.

124	ГЛАВА 3. ОДНОМЕРНЫЕ СТАЦИОНАРНЫЕ ЗАДАЧИ
Плотность вероятности получаем усреднением квадрата высоко-

частотного множителя sin (x)	в (3.58)	по периоду. С учетом sin2		1/ 2
находим
w(x) \|	(x) \|2	1	\| A \|2 .

		2 p(x)
		2 p(x)

Множитель 1/ p связан с тем, что с увеличением скорости уменьшается время пребывания частицы в единичном интервале около рассматриваемой точки.

x2			dx				p
Условие нормировки w dx		1 с учетом p	dx	, dx			p	dt дает
Условие нормировки w dx		1 с учетом p	dt	, dx				dt дает
x1			dt
x1
2		T /2
2		T /2
	\| A \|	dt 1, \| A \|	2			,
2		dt 1, \| A \|	2		T	,
		0

где Т – период движения.

На пути между точками поворота x1

и x2

ВКБ-волна (3.58) набирает

фазу

1 x2

Пройдя замкнутый путь,

волна восстанавливается,

p(x ) dx

и фаза

т2 p(xў) dxў + =

т p(x) dx +

получает приращение

(n +1) , где n = 0,1, 2,...

Для состояния n находим

условие квантования Бора–Зоммерфельда–Крамерса

1 ц

p(x) dx =

2 зn +

(3.59)

(n)

полученное Х. Крамерсом в 1926 г. Условие применимости квазиклассического приближения соответствует большим значениям импульса, что приводит к

большим значениям квантового числа n 1 и к условию квантования Бора–Зоммерфельда (1.17а).

3.6. Одномерное рассеяние

125

Вне классической области E U (x) , поэтому p(x) – мнимая функция.

Оставляя в (3.58) решения, убывающие при удалении от точек поворота, получаем

		A		1	x
(x x2 )	1		exp		\| p(x) \| dx ,	(3.60)

	\| p(x) \|
	\| p(x) \|				x2
					x2

		A		1 x1
(x x1)	2		exp			\| p(x) \| dx .	(3.61)

	\| p(x) \|				x
	\| p(x) \|

3.6. ОДНОМЕРНОЕ РАССЕЯНИЕ

Частица с энергией Е движется вдоль оси x и попадает в область с полем U(x) . Падающая волна рассеивается, возникают отраженная и проходящая

волны. Из уравнения Шрѐдингера (3.2) при x получаем

	k2	0 ,		1				1	p .
			k	1		2 [E U ( )]		1
			k			2 [E U ( )]

Частные решения описывают:
при x	падающую волну с единичной амплитудой
			пад (x		)		eik x
и отраженную волну
			отр (x		)		r e ik x ;
при x	проходящую волну
			пр (x		)		t eik x .

(3.62)

(3.63)

(3.64)

При рассеянии фаза волны изменяется, поэтому амплитуды r и t комплексные.

Используя (2.72) jx	Im	d	, находим проекции плотности тока веро-
		dx

ятности падающей, отраженной и проходящей волн:

126

Глава 3. ОДНОМЕРНЫЕ СТАЦИОНАРНЫЕ ЗАДАЧИ

пад

отр

пр k

| r |

| t | .

(3.65)

Коэффициент отражения (reflection) определяется отношением модулей плотностей токов вероятности отраженной и падающей волн

	\|	jотр \|			\| r \|2	wотр
R(E)							,	(3.66)
	\|	j	пад	\|		пад
						w
тогда
	jотр			R(E) jпад .				(3.67)

Коэффициент прохождения (transmission) определяется аналогично:

| jпр |

| t |2

wпр

T (E)

(3.68)

| jпад |

wпад

тогда

jпр

T (E) jпад .

(3.69)

Условие унитарности. Из уравнения непрерывности тока вероятно-

сти (2.73) следует равенство проекций плотностей токов при x

jпад

jотр

jпр ,

(3.70)

тогда

1 | r |2

| t |2 .

(3.71)

С учетом (3.67) и (3.69) из (3.70) получаем условие унитарности (от лат. unitas

– одно целое):

R(E) T(E) 1

(3.72)

– сумма вероятностей всех возможных процессов в системе, т. е. отражения и прохождения, равна единице при любой энергии.

3.7. Туннельный эффект

127

3.7. ТУННЕЛЬНЫЙ ЭФФЕКТ

Прохождение барьера, недоступного для классической частицы, называется туннельным эффектом. Его исследовал Георгий Антонович Гамов

(1904–1968) в		1928 г. и объяснил парадокс, связанный с		-распадом
U238	Th234	He4	. Два протона и два нейтрона ядра урана объединяются и
92	90	2

образуют -частицу с энергией 4,18 МэВ. Задерживающий потенциал ядра урана составляет 8,57 МэВ. Тем не менее ядро распадается благодаря туннельному эффекту. Термин ввел Вальтер Шоттки в 1931 г.

Одномерный туннельный эффект. Частица с полной энергией Е в

виде плоской волны

1(x) exp px

распространяется вдоль оси x и встречает барьер U (x)						E при x1 x x2 , как
показано на рис. 3.15. Возникает отраженная волна
	2 (x) r exp		i		px .
	2 (x) r exp				px .

	U(x)
1(x)				3(x)		4(x)
						4(x)

2(x)		E
2(x)

	x1 0		x2				x

Рис. 3.15. Туннельный эффект

Внутри барьера, согласно квазиклассическому приближению (3.60), волна экспоненциально затухает:

			c		1	x
3	(x)			exp		\| p(x) \| dx .

		\| p(x) \|
		\| p(x) \|				x1
						x1

128

Глава 3. ОДНОМЕРНЫЕ СТАЦИОНАРНЫЕ ЗАДАЧИ

За барьером

4 (x)

t exp

px .

Коэффициент прохождения барьера. Из (3.68)

при k k

находим

4 ( ) |2

4 (x2 ) |2

3 (x2 ) |2

) |

1(x1) |

3(x1) |

Соотношение

1(x1)

3 (x1)

следует из условия сшивания решений (3.11) при

условии малости отраженной волны. Подставляя

3 (x) в последнюю формулу

и учитывая

| 3 (x1) |2

| c |2

| p(x) |

2 | E U (x) | , | p(x1) |

| p(x2 ) | ,

| p(x1) |

в квазиклассическом приближении с точностью до слабо меняющегося и близкого к единице множителя перед экспонентой, находим

2 x2

T (E) exp

2 | E

U (x) | dx .

(3.73)

Для прямоугольного барьера шириной

x1 l и высотой U0

из (3.73)

получаем

T (E) exp

(U0 E) .

(3.73а)

Точное решение (П.4.7) найдено в примере 4.4. Проницаемость барьера суще-

ственна	при T e 1 , тогда	2l				1,		и это ограничивает ширину
		2l	2	(U0 E)
			2	(U0 E)

барьера
		l					.	(3.74)


			2		2 (U0	E)

3.7. Туннельный эффект

129

Чем меньше масса частицы, тем более широкий и высокий барьер она преодолевает. Коэффициенты прохождения электрона и протона с одинаковой энергией через один и тот же барьер согласно (3.73) отличаются в

e 1840 1018 раза. Для макроскопического тела туннельный эффект не проявляется.

Физическая причина туннельного эффекта основана на соот-

ношении неопределенностей (2.37)

/ 2. Если частица обнаруживается

внутри барьера шириной l, то неопределенность ее положения

l , тогда

неопределенность ее импульса

p ~ / (2l) , что дает дополнительную кинети-

ческую энергию E

(

p)2

. Суммарная энергия E

8 l2

обеспечивает преодоление

барьера

шириной,

описываемой

формулой (3.74).

Сканирующий туннельный микроскоп измеряет микрорельеф

проводящей поверхности. Игла из платины или вольфрама с атомарным острием подводится к поверхности сначала двигателем грубого перемещения, а затем пьезосканером на расстояние ≤1 нм, которое контролируется по величине туннельного тока. На иглу подается потенциал (0,01…10) В по отношению к поверхности. Туннельный ток I через вакуумный промежуток размером l пропорционален коэффициенту прохождения (3.73) и экспоненциально зави-

сит от l. При l ~ 0,1 нм ток I ~ (1 103 ) нА . Перемещение иглы на l ~ 0,1нм

меняет ток в 10 раз. Игла периодически сканирует поверхность. Ток поддерживается на одном уровне за счет перемещения иглы перпендикулярно поверхности. Регистрируемые перемещения иглы дают рельеф поверхности. Изображение графена в туннельном микроскопе показано на рис. 9.1, а. Разрешение по нормали к поверхности достигает 0,005 нм, в плоскости – 0,2 нм, что делает возможным наблюдение отдельных атомов. Малая величина используемого потенциала не разрушает исследуемый объект. Устройство может работать при нормальной температуре, его разработали Герд Биннинг и Генрих Рорер в 1982 г.

130	Глава 3. ОДНОМЕРНЫЕ СТАЦИОНАРНЫЕ ЗАДАЧИ

ПРИМЕРЫ 4

4.1.Найти коэффициент прохождения электрона с энергией Е из металла

ввакуум под действием внешнего электрического поля напряженностью E.

При образовании кристаллической решетки простого металла валентные электроны отрываются от атомов, становятся свободными и при низкой температуре имеют полную энергию E F , где F – энергия Ферми. Ионный ос-

тов занимает около 15 % объема кристалла и образует периодическую структуру. Неоднородности решетки вызывают электрон-ионное рассеяние. Длина

свободного пробега электрона при низкой температуре достигает 109 межатомных расстояний (~1 см). На границе металл–вакуум на электрон действуют возвращающие силы со стороны нескомпенсированных положительных ионов решетки и электронного облака, окружающего металл. Объем металла для электрона является потенциальной ямой

U(x)			с работой	выхода	W 5 эВ .	Тепловая
U(x)
U0	E		энергия kT	0,1 эВ активизирует электро-
			ны вблизи уровня Ферми, и основная масса
W			электронов не может покинуть металл даже
F			при температуре плавления металла. Если
			создать электрическое поле E, направленное
			к металлу, как показано на рис. 3.16, то гра-
			фик потенциальной энергии будет накло-
0	x1	x	няться тем сильнее, чем больше поле. Ши-
Рис. 3.16. Холодная эмиссия			рина потенциального		барьера	становится
Рис. 3.16. Холодная эмиссия			конечной, и	происходит туннельный эф-
электронов из металла			конечной, и	происходит туннельный эф-
электронов из металла			фект, называемый холодная или автоэлек-
			фект, называемый холодная или автоэлек-

тронная эмиссия электронов. Явление обнаружил Роберт Вуд в 1897 г., исследовали Ральф Фаулер и Лотар Нордгейм в 1928 г.

Однородное поле E создает при x					0 распределение потенциала и потен-
циальной энергии электрона
	(x)	(0)	E x , U (x)			e (x) U0 eE x .
Протяженность	барьера		на уровне		Ферми находим из Eкин (x1) 0 ,
E F U (x1)	U0	eE x1 , тогда
			x1	U0	F	W	.
			x1	eE		eE	.
				eE		eE

Примеры 4

131

Из (3.73) получаем

T (

F )

exp

I ,

U (x)

F dx

(U0

F ) eE x dx

x dx .

Заменяя y

x1 x , находим I

2 W 3/2

. Коэффициент прохождения барьера

на уровне Ферми

W 3/2

T (

F )

exp

(П.4.1)

где эффективное задерживающее поле

W 3/2

7, 4 109 (W , эВ)3/2 ,

В/м.

Автоэлектронная эмиссия дает плотность тока до 1010 А/см2, используется в электронных микроскопах, рентгеновских трубках, приемниках инфракрасного излучения.

4.2. Найти коэффициенты отражения и прохождения барьеров, показан-

ных на рис. 3.17, для частицы с энергией E

U0 .

Для барьера на рис. 3.17, а при x

0 и x

0 из (3.1) получаем падающую,

отраженную и проходящую волны

(x) eik1x ,

(x) r e

ik1x ,

(x) t eik2x ,

2 E / ,

2 (E U0 ) / .

Граничные условия (3.11) и (3.12) при x

0 дают

t ,

откуда находим

2k1

(П.4.2)

k1 k2

132

Глава 3. ОДНОМЕРНЫЕ СТАЦИОНАРНЫЕ ЗАДАЧИ

1(x)

U(x)

1(x)

U(x)

3(x)

2(x)

Рис. 3.17. Надбарьерное отражение

Из (3.66) и (3.72) получаем коэффициенты отражения и прохождения

R(E) r2

1 k2 / k1

1 U0 / E

1 k2 / k1

1 U0 / E

T (E)

4k2 / k1

4 1 U0 / E

(1 k2 / k1)2

1 U0 / E )2

При

E U0 происходит полное отражение

R(U0 ) 1. При

E 2U0 находим

0,03. При E U0

разлагаем решение в ряд и получаем

R(E U0 )

Замена k1 k2 преобразует рис. 3.17, а в рис. 3.17, б, при этом

r , t

2k2

t ,

(П.4.3)

функции R(E) и T(E) не изменяются. Обращение движения частицы через любой барьер не изменяет коэффициенты отражения и прохождения.

4.3. Амплитуды прохождения t и отражения r через систему локальных барьеров 1 и 2, показанную на рис. 3.18, выразить через амплитуды прохождения t1 , t2 и отражения r1 , r2 каждого из барьеров по отдельности. Между

барьерами расстояние a, волновое число частицы k. При распространении волн сохраняется фазовая когерентность.

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 3613 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в папке Лекции Квант.мех. СГФ

#
11.03.20164.25 Mб2432014_krasnop.pdf
#
11.03.201613.88 Mб241Квант. мех..pdf
#
11.03.20164.98 Mб94Квант.лекция 0.doc
#
11.03.20169.91 Mб137Квант.лекция 1.doc
#
11.03.20161.84 Mб129Квант.лекция 2.doc
#
11.03.20165.14 Mб119Квант.лекция 3.doc
#
11.03.2016452.61 Кб89Квант.лекция 4-1.doc