Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Новосибирский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Лекции Квант.мех. СГФ / Квант. мех

..pdf

Скачиваний:

239

Добавлен:

11.03.2016

Размер:

13.88 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 3612 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

3.4. Линейный гармонический осциллятор

113

n квантов с одинаковой энергией. Методы описания осциллятора использ у- ются для квантования электромагнитного поля в резонаторе и в свободном пространстве, где поле рассматривается как система гармонических осцилляторов.

Осциллятор в классической теории. Материальная точка массой

µ находится во внешнем поле с потенциальной энергией U(x) , имеющей минимум при x 0 :

				U(0)	0 ,			U (0) 0 ,										U (0)					0 .
Вблизи x	0 заменяем функцию рядом Маклорена и ограничиваемся первыми
тремя слагаемыми
						U (x) U (0)									x2				1	x2 .
						U (x) U (0)									2		2			x2 .
															2		2
Квазиупругая сила				f	dU / dx							x вызывает ускорение x . Второй закон
Ньютона	x f	дает уравнение гармонического колебания
		2	x	0 ,												x(t)				xmax cos( t						0 ) .
		2						/			,
	x							/			,
Потенциальная энергия получает вид
															2			x2 .
								U (x)																		(3.23)
								U (x)							2											(3.23)
															2
При максимальном отклонении полная энергия E																							U (xmax ) , тогда

				E	1			2 x2			,					x				1				2E	.	(3.24)
				E				2 x2			,					x									.	(3.24)
					2				max							max
					2
Осциллятор в квантовой теории. Гамильтониан и уравнение Шрѐ-
дингера (3.1) имеют вид
							ˆ			2			d 2				2				2	,				(3.25)
						H														x
						H		2				dx2					2			x
								2				dx2					2
								2 E			2				2			x2
					(x)			2 E													(x) 0 .					(3.26)

								2						2
								2						2

114 ГЛАВА 3. ОДНОМЕРНЫЕ СТАЦИОНАРНЫЕ ЗАДАЧИ

Переходим к безразмерному аргументу

(3.27)

и получаем

2 d 2

d 2

dx2

x02

dz2

(3.28)

(z) (1

z2 )

(z) 0 ,

(3.29)

(3.30)

Волновые функции. Сравниваем (3.29) с уравнением обобщенного

гипергеометрического типа (С.1) в приложении 3 и находим:

f0 1,

a b 0 , Q 2 n 1

2s ,

0 ,

1 . Существование набора орто-

нормированных решений дает s

0, 1, 2,... , тогда

1, Q

1. Из (С.2) и

(С.3)

получаем

0 ,

z ,

(z) 1

и решение в виде функции

Гаусса–Эрмита

n (z)

An e

ˆ n

An ( 1)

Hn (z) ,

где Hn (z)

– полином Эрмита. Из (С.7) и (С.9) находим условие ортонорми-

рованности

n dz

n,n

| An |2

2n n! .

(3.31)

Если

не

целочисленное,

то

при

решение

имеет

вид

) ~ exp(z2 / 2)

и условие нормировки

|2 dz

не существует.

При

( 1)n

1/2 2n n! x

1/2

получаем

n (z)	1		Hn (z) e z		2	/2
						/2


	2n 1/2n!x
		0
		n (z,t)		n (z) e

			1	Hn (z) 0	(z),


			2n n!
			2n n!		(3.32)
					(3.32)
i	E t
	E t
		n	.
			.

3.4. Линейный гармонический осциллятор

115

Учитывая H

(z)

H (z)

2z ,

(z) 4z2

2 , из (3.32) находим основное и

первые возбужденные состояния

0 (x)

exp

2x02

1/2 x

1(x)

exp

0 (x) ,

(3.32а)

2x02

1/2 x0 x0

2 (x)

1 exp

0 (x) ,

x02

2x02

x02

1/2 x

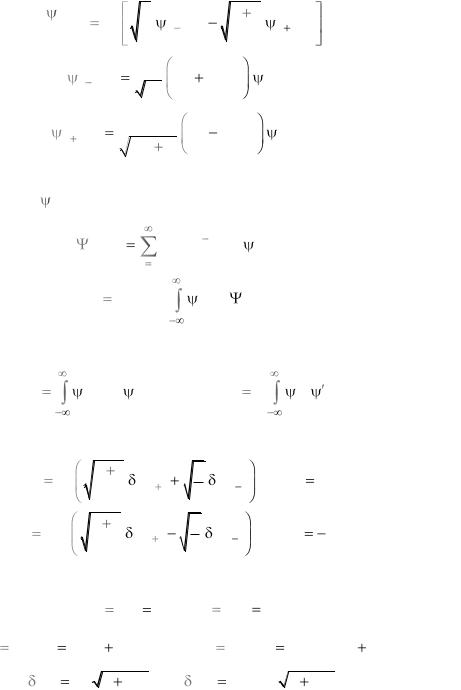
показанные на рис. 3.13.

			U(x)
	E2				2(x)
					2(x)
h	E1
	E1				1(x)
					1(x)
h	E0
	E0				0(x)
h					0(x)
h
x1	x0	0	x0	x1	x
Рис. 3.13. Гармонический осциллятор

Ортонормированность, полнота и рекуррентные соотноше-

ния для волновых функций следуют из (3.31) и теории полиномов Эрмита [9]

x0 n (z) m (z) dz n,m , n (x) m (x) dx n,m , (3.33)

		n (x)		n ( y) (x y) ,
n	0

x n (x)	x0		n 1		n 1(x)	n	n 1(x) ,	(3.34)

		2				2
		2				2

116	ГЛАВА 3. ОДНОМЕРНЫЕ СТАЦИОНАРНЫЕ ЗАДАЧИ

d n (x)

n 1(x)

(x)

n 1

n 1(x)

2(n

1) x0

		n 1			n 1(x) .	(3.35)

2

x0	d				n (x) ,

	dx
x0				d	n (x) ,	(3.35а)

			dx

Общее решение волнового уравнения Шрѐдингера разлагается по ортонормированному базису{ n (x)} :

(x, t)		cn (t) e	iEnt /	n (x),

	n	0		(3.36)

cn (t) e	i (En / )t
		n (x)		(x, t) dx.

Матричные элементы

xnm	*
	n

(x) x m (x) dx , pmn		m n dx
	i

находим, используя (3.33)–(3.35):

xmn		x0		n	1

					2
					2

p	i		n		1
p	i
mn		x0	2
		x0	2

m,n 1

m,n 1	,	xmn	xnm ,
			(3.37)
m,n 1	,	pmn	pnm .

Для средних значений и флуктуации в состоянии n получаем

xnn 0 ,

pnn 0 ,

(x2 )

1 / 2) ,

( p2 )

( / x )2

(n 1 / 2)

, (3.38)

( x)n

n 1 / 2 ,

( p)n

( / x0 ) n 1/ 2 .

3.4. Линейный гармонический осциллятор

117

Энергия состояния s n	0,1, 2,... следует из (3.30):
E		n		1	.	(3.39)

n			2

Спектр эквидистантный
En 1 En			.

Номер состояния n равен числу квантов энергии , связанных с осцилля-

тором. Переход к соседнему состоянию добавляет или удаляет квант энергии.

Энергия основного состояния

E0 / 2

является минимальной энергией осциллятора. Отсутствие состояния покоя у пространственно ограниченной системы следует из соотношения неопределенностей Гейзенберга (2.37). Для флуктуаций в основном состоянии из (3.38) получаем

( x)		x	0	,	( p)				,		( p)			( x)		1	,
( x)	0			,	( p)	0			,		( p)		0	( x)	0	2	,
	0	2				0	2	x0					0		0
		2					2	x0
						2	2
					p 0		2			2		1
			E0		p 0				x	2		1	.
			E0		2		2		x	0	2		.
					2		2				2

Границы классического движения или точки поворота xn осцил-

лятора с энергией En

соответствуют

U (x )

где использовано (3.23) и (3.27). Учитывая (3.39), получаем

1 .

(3.40)

Величина (3.27) x0

является амплитудой вакуумных колебаний в

основном состоянии. Из рис. 3.13, где показаны x0, x1 и графики волновых функций, следует возможность обнаружения осциллятора за пределами области классического движения, что является туннельным эффектом.

118 ГЛАВА 3. ОДНОМЕРНЫЕ СТАЦИОНАРНЫЕ ЗАДАЧИ

Операторы рождения и уничтожения кванта. Записываем

(3.35а) в виде

n 1(x)	1		aˆ		n (x),


		n
n 1(x)	1			aˆ	n (x),


	n 1
	n 1

где операторы понижения и повышения порядка функции

aˆ

pˆ ,

0 dx

aˆ

pˆ .

0 dx

Тогда получаем

aˆ

n 1,

n 1

n 1,

(aˆ aˆ ),

pˆ

(aˆ aˆ ).

i 2 x0

Вводим оператор порядка функции

1 pˆ 2

1 1

N aˆ aˆ

n ,

0, 1, 2,...

Из (3.43) и (3.44) находим

[aˆ, aˆ

]

aˆ

[N, aˆ

[N, aˆ]

aˆ, N N,

aˆ aˆ

(aˆ aˆ aˆ aˆ ),

aˆ ,

aˆ.

[H , aˆ ]

[H , aˆ]

(3.41)

(3.42)

(3.43)

(3.44)

(3.45)

(3.46)

3.4. Линейный гармонический осциллятор			119
Учитывая, что	– энергия кванта,		n – состояние осциллятора с n квантами,
		ˆ
из (3.43) и (3.44) получаем: N – оператор числа квантов, aˆ – оператор
рождения кванта,	aˆ	– оператор уничтожения кванта. Основное состояние
0 с энергией E0		/ 2 не содержит квантов и называется состоянием ва-

куума. Действуя операторами рождения и уничтожения на состояние вакуума, из (3.43) получаем

n (x)	1		(aˆ )n	0 (x) , aˆ	0 0 .	(3.47)


		n!

Из (3.47) с учетом (3.42) находим основное и возбужденные состояния. Соотношения (3.32а) и (3.41)–(3.47) следуют также из результатов примера 2.21 с

параметрами: , , b x0 / 2 , c 0 .

Трехмерный гармонический осциллятор с потенциальной энер-

гией

U (x, y, z)

12 x2

22 y2

32 z2

описывается уравнением

2 E

x (x, y, z) .

xi2

i 1

Переменные разделяются:

(x, y, z)

1(x)

2 ( y) 3 (z) ,

E E1 E2 E3 ,

для каждой оси получается уравнение одномерного гармонического осциллятора. Из (3.39) находим

E	n	n	n	1	(				)	,	n 0, 1, 2,...	(3.48)
						1	2	3
n,m,l	1 1	2 2	3 3	2							i

Изотропный осциллятор имеет		1 2 3	и потенциальную
энергию U	2r2 / 2 , поэтому называется сферическим осциллятором. Из
(3.48) получаем
	EN (N	3 / 2) ,	(3.49)

120			ГЛАВА 3. ОДНОМЕРНЫЕ СТАЦИОНАРНЫЕ ЗАДАЧИ
где N n1	n2 n3	0, 1, 2,... Кратность вырождения gN			уровня N равна числу
способов,	которыми N разбивается на целые числа n1, n2 , n3 . В частности,
g0 1, g1	3 , g2	6 и
		gN	1	(N 1)(N 2)	(3.50)
		gN	2	(N 1)(N 2)	(3.50)
			2

–в общем случае

3.5.КВАЗИКЛАССИЧЕСКОЕ КВАНТОВАНИЕ ВКБ

Аналитическое и точное решение уравнения Шрѐдингера возможно для ограниченного числа функций потенциальной энергии. Квазиклассическое квантование является приближенным методом. Фазу волновой функции разлагаем в ряд по степени малости и ограничиваемся первыми двумя слагаемыми. Это допустимо, если длина волны де Бройля частицы гораздо меньше расстояния существенного изменения потенциальной энергии. Малая длина волны соответствует большому импульсу и квазиклассическому поведению частицы. Метод дает уровни энергии и волновые функции стационарных состояний одномерного движения. В первом приближении получается квантование Бора–Зоммерфельда. В ряде случаев метод применим для трехмерных систем. Квазиклассическое квантование разработали Грегор Вентцель, Хендрик Крамерс и Леон Бриллюэн в 1926 г., и оно называет-

ся методом ВКБ.

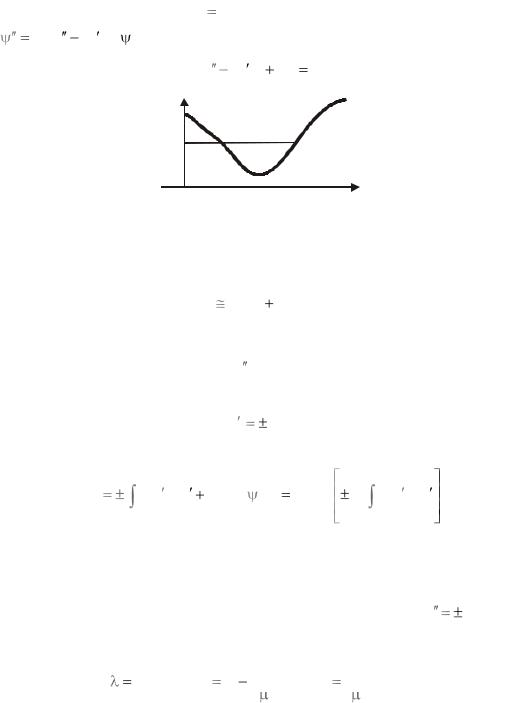
Уравнение состояния. Частица с полной энергией Е находится в потенциальной яме с плавной конфигурацией U(x) , показанной на рис. 3.14. Используем (3.1)

				2	p2	0 ,		(3.51)
где	p(x)		2 [E U (x)] – импульс частицы. Между точками					поворота
x1	x x2	классического движения решение ищем в виде волны
						i
					A e		S ( x) ,
				(x)	A e		S ( x) ,	(3.52)

3.5. Квазиклассическое квантование ВКБ										121
где S(x) – комплексная фаза;			A	const . Подставляем (3.52) в (3.51) и с учетом
2	[i S (S )2 ]	получаем нелинейное уравнение
		i S			(S )2 p2		0 .			(3.53)
		U(x)
		E
		E

		0		x1		x2		x
		Рис. 3.14. Потенциальная яма
Решаем (3.53) посредством разложения S(x)							в ряд по степеням , ограничи-
ваясь двумя слагаемыми
		S (x)			S1(x) S2 (x) .
	Первое приближение. Изменение S(x) считаем медленным
				\| S		\| p2 .
Из (3.53) получаем
					S1	p .				(3.54)
Интегрирование дает
	x							i x
	S1(x)	p(x ) dx	c1 ,			(x)	A exp		p(x ) dx .	(3.55)
	S1(x)	p(x ) dx	c1 ,			(x)	A exp		p(x ) dx .	(3.55)
	x							x
	1							1

Фаза волновой функции определяется интегралом от импульса по пути между точкой поворота и текущим положением частицы, что соответству-

ет условию квантования Бора–Зоммерфельда (1.17).

Условие применимости решения. Учитывая (3.54) S

и ис-

пользуя

| p |

U (x) E

122

ГЛАВА 3. ОДНОМЕРНЫЕ СТАЦИОНАРНЫЕ ЗАДАЧИ

из | S

| p2 получаем

| p |3 .

(3.56)

Согласно (3.56) U(x) изменяется медленно. Разлагаем ее в ряд Тейлора около точки поворота x1 и ограничиваемся двумя слагаемыми

U (x) U (x )

(x x ) E

(x x ) ,

E U (x)

| x x | ,

где | x

x1 | – расстояние от точки поворота до области, где применимо (3.56).

Используя (3.56), находим

p2 2 (E U )

| x x |

| p |3 | x x |,

| p |

2 | x x1 |

Из

h / p и (3.56) получаем

1/3

4 | x x | ,

| x

x |

(3.57)

dU / dx

Квазиклассическое приближение применимо, если длина волны гораздо меньше расстояния, на котором существенно изменяется потенциальная энергия. Это соответствует большому импульсу и его малому изменению на протяжении указанного расстояния. Решение ВКБ неприменимо вблизи точки поворота, где

	2	1/3
\| x x1 \|			,	p 0 ,	.
	dU / dx

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 3612 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в папке Лекции Квант.мех. СГФ

#
11.03.20164.25 Mб2392014_krasnop.pdf
#
11.03.201613.88 Mб239Квант. мех..pdf
#
11.03.20164.98 Mб94Квант.лекция 0.doc
#
11.03.20169.91 Mб136Квант.лекция 1.doc
#
11.03.20161.84 Mб129Квант.лекция 2.doc
#
11.03.20165.14 Mб118Квант.лекция 3.doc
#
11.03.2016452.61 Кб89Квант.лекция 4-1.doc