
- •ОГЛАВЛЕНИЕ
- •Введение
- •Основные положения
- •1.1. Вероятность случайного события
- •1.2. Теоремы о вероятности
- •1.3. Характеристики случайной дискретной величины
- •Относительная флуктуация
- •1.4. Характеристики случайной непрерывной величины
- •1.5. Биномиальное распределение
- •1.6. Распределение Пуассона
- •1.7. Нормальное распределение
- •Результаты (1.44) и (1.45) совпадают с выражениями (1.36) и (1.37) для распределения Пуассона. Из (1.41) и (1.45) получаем плотность вероятности в виде
- •Примеры 1
- •СТАТИСТИЧЕСКАЯ ФИЗИКА КЛАССИЧЕСКИХ СИСТЕМ
- •2.1. Фазовое пространство системы частиц
- •2.2. Число микросостояний
- •2.3. Энергетическая плотность состояний
- •2.4. Характеристики макросостояния
- •2.6. Теорема Лиувилля
- •Аналогично течет несжимаемая жидкость, сохраняя свою плотность. Теорема используется для получения функции распределения состояний по фазовому пространству. Теорему доказал Ж. Лиувилль в 1838 г.
- •2.7. Микроканоническое распределение
- •Примеры 2
- •2.8. Каноническое распределение
- •Примеры 3
- •2.10. Распределение тепловой энергии по степеням свободы
- •Примеры 4
- •2.11. Распределение Максвелла
- •2.12. Поток частиц
- •Примеры 5
- •Задачи 1
- •2.13. Распределение Больцмана
- •Примеры 6
- •2.14. Химический потенциал и активность
- •2.15. Распределение частиц по состояниям.
- •2.17. Большое каноническое распределение
- •Примеры 7
- •2.18. Условия применимости классической статистической физики
- •Задачи 2
- •3.1. Плотность состояний частицы
- •Примеры 8
- •3.2. Каноническое распределение квантового газа
- •Примеры 9
- •СТАТИСТИЧЕСКИЕ РАСПРЕДЕЛЕНИЯ ГАЗОВ ФЕРМИОНОВ И БОЗОНОВ
- •4.1. Большое каноническое распределение квантовой системы
- •Результат выражается через статистическую сумму (4.9)
- •4.2. Распределение фермионов
- •4.3. Распределение бозонов
- •Объединенное распределение по состояниям имеет вид
- •Если бы принцип Паули не действовал, то для получения энергии Ферми потребовалась бы температура, называемая температурой Ферми:
- •Рис. 4.8. Ферми-поверхность металлов: (а) – Na, (б) – Cu, (в) – Cs
- •4.6. Распределение Ферми–Дирака для f-мерного газа
- •4.7. Двухмерный электронный газ
- •4.8. Одномерный электронный газ
- •4.9. Баллистический проводник
- •4.10. Сканирующий туннельный микроскоп
- •Примеры 10
- •4.11. Фотонный газ
- •Концентрация фотонов со всеми частотами
- •Вычисляем интеграл по формуле
- •Получаем
- •Примеры 11
- •4.12. Фононный газ
- •Примеры 12
- •4.13. Конденсация Бозе–Эйнштейна
- •Примеры 13
- •Задачи 3
- •ПРИЛОЖЕНИЯ
- •1. Физические постоянные
- •Постоянная Больцмана
- •Число Авогадро
- •Газовая постоянная
- •Постоянная Планка
- •Масса свободного электрона
- •Заряд электрона
- •Магнетон Бора
- •2. Интегралы классической статистики
- •3. Интегралы квантовой статистики
- •4. Суммы рядов
- •БИБЛИОГРАФИЧЕСКИЙ СПИСОК
- •ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ

ПРИМЕРЫ 13
пучок втягивается в узлы стоячей волны. Возникает решетка линий, на которых резко возрастает число осажденных атомов. Две взаимно перпендикулярные стоячие волны создают решетку точек сгущений атомов. Наименьший полученный размер узла наноструктуры ~15 нм.
Используются также маски размером ~10 мкм вместе с камерой-
обскурой, уменьшающей изображение маски в ~104 раз до ~10 нм. Из
атомов рубидия получен когерентный пучок с поперечным сечением ~1 нм. Это позволяет размещать атомы на подложке с высокой точ-
ностью.
Атомтроника использует БЭК и лазерные лучи для управления и контроля потоком атомов, где их роль аналогична роли электронов в электронике. Отталкивание между атомами делает их поведение аналогичным поведению фермионов, вызванному принципом Паули. Цепочка потенциальных ям оптической решетки с разной заселенностью атомами БЭК, которые туннелируют между ямами, работает аналогично диоду и транзистору – выключателю и усилителю. Сверхтекучесть атомов БЭК приводит к отсутствию сопротивления цепи. Такие устройства могут использоваться для квантовой обработки информации. БЭК в кольцевом канале является высокочувствительным сенсором вращения. В высоком вакууме в кольцевой ловушке диаметром 40 мкм, созданной методом нарисованного потенциала, вращаются как
единое целое с общей волновой функцией сотни тысяч атомов БЭК при температуре в нанокельвины. В двух местах кольца сделаны потенциальные барьеры путем снижения интенсивности лазерного луча в этих точках. Один из барьеров перемещается, в результате распределение атомов по кольцу изменяется, что позволяет измерить перемещение (An atomic SQUID / C.A. Sackett // Nature. – 2014. – Vol. 505. – Р. 166).
Примеры 13
13.1. Для слабо вырожденного свободного трехмерного бозонного газа при TC <T ≤| µ | /k найти химический потенциал и теплоемкость.
Из (П.10.21) получаем
µ µкл − 2kT3/2 eµкл/kT ,
363

Г л а в а 4. СТАТИСТИЧЕСКИЕ РАСПРЕДЕЛЕНИЯ ГАЗОВ ФЕРМИОНОВ И БОЗОНОВ
где для классического газа согласно (4.31) и (4.32)
µкл = −kT ln NS (2πmkT )3/2 ,h3n
|
eµкл/kT = |
|
h3n |
|
. |
||||
|
|
|
NS (2πmkT )3/2 |
|
|
|
|||
Используя (4.143) в виде |
|
|
|
|
|
|
|
|
|
3 |
n |
|
|
T0 |
|
3/2 |
|||
|
h |
|
= |
|
|
, |
|||
|
NS (2πmkT )3/2 |
0,527 T |
|||||||
|
|
|
|
||||||
выражаем химический потенциал при T >TC через температуру порога конденсации TC :
|
|
3 |
|
0,527 T |
|
|
|
TC |
|
|
3/2 |
|
|
|||
µ(T ) = −kT |
|
|
|
|
|
|
(П.13.1) |
|||||||||
2 ln |
|
T |
|
+ |
1,054 T |
|
|
|||||||||
|
|
|
. |
|||||||||||||
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Для получения теплоемкости |
используем |
|
внутреннюю |
энергию |
||||||||||||
(П.10.22) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
n |
|
|
|
|
|
|
|
|
U 3 kTN 1− |
|
h |
|
|
|
. |
|
|
|
|||||||
|
|
|
|
|
|
3/2 |
|
|
|
|||||||
2 |
|
|
|
|
2NS (4πmkT ) |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||||
При T >TC получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C ≡ dU |
3 kN + |
|
3h3k nN |
. |
(П.13.2) |
||
|
|
||||||
V |
dT |
2 |
|
8NS (4πmkT )3/2 |
|
|
|
|
|
|
|
||||
При T <TC используем (4.152) |
|
|
|
|
|
||
|
C = |
79 k5/2 |
N |
S |
m3/2 V T 3/2 . |
|
|
|
V |
h3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Объединение результатов дает зависимость теплоемкости от темпера-
туры, показанную на рис. 4.36. При температуре порога БЭК
364
ПРИМЕРЫ 13
существует пик теплоемкости, производная испытывает скачок. Это вызвано тем, что увеличение темпера-
туры при T <TC приводит к росту за-
трат энергии в связи с увеличением числа частиц в газовой фазе. При
T >TC теплоемкость уменьшается с
увеличением температуры за счет взаимного «притяжения» бозонов.
CV1,92/kN















1,5 















|
|
|
T |
0 |
TС |
||
Рис. 4.36. Теплоемкость бозе-газа
13.2. Найти температурную зависимость химического потенциала свободного трехмерного бозонного газа вблизи порога конденсации.
∞ |
|
|
|
|
|
|
|
|
|
ε |
|
|
|
||
При T ≥TC число частиц газа (4.138) N = a ∫ |
|
|
|
|
dε, где |
||
e |
(ε−µ)/kT |
−1 |
|||||
0 |
|
|
|
|
|||
a = 2hπ3 NSV (2m)3/2 . Добавляем в газ столько частиц, что он начинает
конденсироваться при температуре Т, тогда N1 = a ∞∫ ε/kTε dε. Вбли-
0 e −1
зи порога конденсации | µ | мало, и основной вклад в интегралы вносит ε << kT . Разлагаем экспоненты в ряд
1 |
|
− |
|
|
1 |
|
|
1 |
|
− |
1 |
|
= |
kT | µ | |
||||
|
eε/kT −1 |
|
|
e(ε−µ)/kT −1 |
|
|
ε / kT |
|
|
(ε−µ) / kT |
|
|
(ε+ | µ |)ε |
|||||
и получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
dε |
|
|
|
|
|
|
|
|
|
|
|
N1 − N akT | µ | |
|
. |
|
|||||||||
|
|
|
|
|
|
(ε+ | µ|)ε1/2 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
0∫ |
|
|
|
||||
Интеграл равен |
|
|
π |
|
|
, тогда |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
| µ | |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
N1 − N πakT 
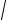 | µ| ,
| µ| ,
µ(T ) − (πakT1 )2 (N1 − N )2 .
365

Г л а в а 4. СТАТИСТИЧЕСКИЕ РАСПРЕДЕЛЕНИЯ ГАЗОВ ФЕРМИОНОВ И БОЗОНОВ
Вблизи порога конденсации используем (4.140)
N 2,314 a (kT |
)3/2 , |
N 2,314 a (kT )3/2 |
, |
C |
|
1 |
|
и при (T −TC ) <<TC получаем параболическую зависимость
|
(T 3/2 |
−T 3/2 )2 |
|
(T −T |
)2 |
|
µ(T ) −0,543k |
|
C |
−1, 22 k |
C |
|
, (П.13.3) |
|
T 2 |
TC |
|
|||
|
|
|
|
|
показанную на рис. 4.32. При выводе последнего равенства использовано
T−TC ≡ ∆, T 3/2 = (TC + ∆)3/2 =TC3/2 (1+ ∆ / TC )3/2 TC3/2 + 32 ∆ TC1/2 .
13.3.Найти температуру порога конденсации TC и число конденсированных частиц при T ≤TC для бозонного газа с числом частиц N, удерживаемых гармонической ловушкой с потенциальной энергией
u(r) = (k x2 |
+ k |
2 |
y2 + k z2 ) / 2 , считая электрохимический потенциал |
1 |
|
3 |
пренебрежимо малым (µ′ = 3 ω/ 2 << kTC ) .
Для рассматриваемой системы используем плотность состояний
(П.8.4)
g(ε) = γε2 ,
где
|
NS |
|
|
|
(k1 k2 k3)1/6 |
|
|||
γ = |
|
|
, |
ω = |
|
|
|
. |
|
2( ω) |
3 |
|
1/2 |
|
|||||
|
|
|
|
|
m |
|
|||
Из (4.147) получаем |
|
|
|
|
|
|
|
|
|
|
kTC = |
|
|
N |
|
1/3 |
|
||
|
ω |
|
|
|
. |
(П.13.4) |
|||
|
|
|
|
||||||
|
|
|
|
1,202 NS |
|
||||
Сравнение (П.13.4) с (4.141) показывает, что для частиц в ловушке температура конденсации растет медленнее с увеличением числа ча-
стиц по сравнению со |
свободным газом. |
Слабость ловушки |
ω<< 2kTC / 3 с учетом |
(П.13.4) выполняется |
при числе частиц |
366

ПРИМЕРЫ 13
N >> 4NS . Число конденсированных частиц при T ≤TC находим из
(4.148)
NC (T ) = N 1−(T / TC )3 .
13.4. Нерелятивистский свободный двухмерный газ состоит из N бозонов массой m, находящихся на площади S и занимающих нижнюю зону размерного квантования. Найти химический потенциал при температуре Т.
Плотность состояний двухмерного нерелятивистского газа находим из (3.17) g = 2πhN2 S Sm . Из (3.3) и (4.18) получаем число частиц газа
∞ |
|
dε |
|
|
|
|
N = g ∫ |
|
|
|
. |
(П.13.5) |
|
e |
(ε−µ)/kT |
−1 |
||||
0 |
|
|
|
|||
От температуры N не зависит, поэтому при уменьшении T уменьшается модуль химического потенциала. Интеграл вычисляем заменой
e(ε−µ)/kT = z , dε = kT dz / z , находим
N/ g =| µ | −kT ln(e|µ|/kT −1) .
Вотличие от трехмерного случая значение µ = 0 не достижимо при
конечной температуре из-за расходимости интеграла (П.13.5) на нижнем пределе.
При | µ | << kT разлагаем экспоненту в ряд и используем
ln(ex −1) |
|
|
|
|
x |
|
|
|
|
|
|
|
x |
|
|
x |
|
|
||
ln x 1+ |
|
|
|
= ln x +ln 1 |
+ |
|
|
|
|
|
|
+ln x , |
||||||||
2 |
|
2 |
|
2 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
| µ | |
|
| µ | |
|
|
|
|
|
|
|
|
kT |
|
||||
|
|
|
= |
|
|
|
|
−kT ln |
|
kT ln |
|
|
, |
|||||||
|
|
g |
|
2 |
|
|||||||||||||||
|
|
|
|
|
|
kT |
|
|
|
|
|
|
|
|
|
| µ | |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
||
|
|
|
|
|
|
µ −kT exp |
− |
|
|
|
. |
|
|
|
||||||
|
|
|
|
|
|
|
gkT |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
x =| µ | /kT .
(П.13.6)
367

Г л а в а 4. СТАТИСТИЧЕСКИЕ РАСПРЕДЕЛЕНИЯ ГАЗОВ ФЕРМИОНОВ И БОЗОНОВ
Химический потенциал свободного двухмерного газа при любом числе частиц стремится к нулю только при T → 0 и бозе-конденсация при конечной температуре отсутствует. Это показал P.C. Hohenberg в 1967 г. для двухмерного и одномерного газа.
13.5. |
Двухмерный бозонный газ с числом частиц N удерживается |
|||||
ловушкой |
с потенциальной энергией |
u(r) = (k x2 |
+ k |
2 |
y2 ) |
2 . Найти |
|
|
1 |
|
|
|
|
температуру порога конденсации TC и число конденсированных частиц при T ≤TC , считая электрохимический потенциал пренебрежимо
малым (µ′ = ω<< kTC ) .
Для газа в ловушке используем плотность состояний (П.8.3)
g(ε) = γε, |
|
NS |
|
|
|
(k1 k2 )1/4 |
|
γ = |
|
|
, ω = |
|
. |
||
( ω) |
2 |
1/2 |
|||||
|
|
|
|
|
m |
||
Из (4.147) получаем |
|
|
|
|
|
|
|
kT |
= |
ω |
6N 1/2 . |
|
(П.13.7) |
||
C |
|
|
|
|
|
||
|
|
π |
NS |
|
|
||
В отличие от свободного двухмерного газа, рассмотренного в приме-
ре 13.4, в 2D-системе с пространственным ограничением БЭК происходит при конечной температуре. Слабость ловушки ω<< kTC с
учетом (П.13.7) выполняется при N >> π2NS / 6 . Число конденсированных частиц при T ≤TC находим из (4.148)
N |
|
(T ) = N |
|
−(T / T ) |
2 |
|
. |
|
|
|
|||
C |
1 |
|
|
|
|
|
|||||||
|
|
|
|
C |
|
|
|
|
|
||||
13.6. Для одномерного бозонного газа с числом частиц N в ло- |
|||||||||||||
вушке с потенциальной энергией |
u(x) = q | x |a |
найти температуру TC |
|||||||||||
порога конденсации и число конденсированных частиц при T ≤TC , |
|||||||||||||
полагая µ′ 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
Плотность состояний системы получаем из (П.8.7) |
|
||||||||||||
|
|
|
2 Γ(1/ a) |
|
|
|
|
|
|
NS |
|
||
1/a−1/2 |
|
|
|
|
|
|
|
2πm |
|
||||
g(ε) = γ ε |
|
|
, γ = |
|
|
|
. |
||||||
|
|
Γ(1/ a +1/ 2) |
|
|
h a q1/a |
||||||||
368
ПРИМЕРЫ 13
Температура конденсации TC входит в формулу для числа частиц газовой фазы
|
|
∞ |
g(ε) dε |
|
|
|
|
∞ 1/a−1/2 |
dε . |
|
|
||||||||
|
N = ∫ |
|
= γ ∫ |
ε |
ε/kT |
|
|
|
|||||||||||
|
ε/kT |
|
e |
|
|
|
|||||||||||||
|
|
0 |
e |
C −1 |
0 |
C −1 |
|
|
|
||||||||||
Используя (4.104), |
вычисляем |
|
интеграл |
(kT |
)1/a+1/2 Γ(1/ a +1/ 2) × |
||||||||||||||
×ζ(1/ a +1/ 2) и получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
1 |
|
1 |
|
1 |
|
|
|
|
NS |
|
|
|
|
|
||||
|
|
|
|
|
2πm |
|
|
1/a+1/2 |
|
|
|||||||||
N = 2 |
Γ |
|
ζ |
+ |
|
|
|
|
|
|
|
|
|
(kTC ) |
|
. |
(П.13.8) |
||
2 |
|
h a q1/a |
|
||||||||||||||||
|
a |
|
a |
|
|
|
|
|
|
|
|||||||||
Для дзета-функции учитываем ζ(1) = ∞ и ζ(x) < 0 |
при x <1. Тогда ко- |
||||||||||||||||||
нечность и положительность значений N и TC ограничивает параметры |
|||||||||||||||||||
удерживающего потенциала: q > 0 , |
0 < a < 2 . Конденсация невозмож- |
||||||||||||||||||
на для свободного газа, что соответствует q = 0 , а также для газа в п а- раболической ловушке с a = 2 . Число конденсированных частиц при T ≤TC находим из (4.147)
N |
|
(T ) = N |
|
/ T |
1/a+1/2 |
|
. |
(П.13.9) |
C |
1−(T |
) |
|
|||||
|
|
|
C |
|
|
|
||
13.7. Выразить число частиц N, внутреннюю энергию U и Ω- |
||||||||
потенциал бозонного газа с активностью |
A ≡ eµ/kT |
при температуре T |
||||||
через спектр энергии частицы {εm}.
Среднее число бозонов (4.18) на уровне m = 0,1,... ∞ выражаем че-
рез активность газа A = eµ/kT : |
|
|
|
|
|
|
|
||
n(εm ) = |
1 |
|
= |
A e−εm /kT |
= |
|
1 |
−1 |
= |
|
|
|
|
− A e−εm /kT |
|||||
|
A−1eεm /kT −1 1− A e−εm /kT |
1 |
|
|
|||||
∞∞
=∑ Ane−nεm /kT −1 = ∑ Ane−nεm /kT .
n=0 n=1
Получаем
∞ |
∞ |
∞ |
|
∂ln Z |
Б |
|
|
|
|
|
|
||||
N(A,T ) = ∑ n(εm ) = ∑ An |
∑ e−nεm /kT = A |
|
|
, |
|||
∂A |
|
||||||
m=0 |
n=1 |
m=0 |
|
|
T |
|
|
369

Г л а в а 4. СТАТИСТИЧЕСКИЕ РАСПРЕДЕЛЕНИЯ ГАЗОВ ФЕРМИОНОВ И БОЗОНОВ
|
∞ |
|
|
|
|
|
|
|
|
|
|
U (A,T ) = ∑ εm n(εm ) = |
|
|
|
|
|
||||
|
m=0 |
|
|
|
|
|
|
|
|
|
∞ |
∞ |
|
∂ln Z |
|
|
|
|
|||
= ∑ An |
∑ εm e−nεm /kT |
= kT 2 |
Б |
, |
(П.13.10) |
|||||
|
|
|
|
|||||||
|
∂T |
|
||||||||
n=1 |
m=0 |
|
|
|
A |
|
|
|||
где статистический интеграл большого канонического распределения бозонов
∞ |
A |
n |
∞ |
|
∞ |
|
|
||
ln ZБ(A,T ) ≡ ∑ |
|
∑ e−nεm /kT = − ∑ ln(1− Ae−εm /kT ) . (П.13.11) |
|||||||
n |
|||||||||
n=1 |
m=0 |
m=0 |
|
||||||
Из (2.183) и (П.13.11) находим (П.10.46) |
|
|
|
|
|
||||
|
|
|
∞ |
A |
n |
∞ |
|
||
ΩB = −kT ln ZБ(A,T ) ≡ −kT ∑ |
|
|
∑ e−nεm /kT = |
|
|||||
n |
|
||||||||
|
|
|
n=1 |
m=0 |
|
||||
|
|
|
∞ |
|
|
|
|
|
|
= kT ∑ ln(1− Ae−εm /kT ) . |
(П.13.12) |
||||||||
m=0
Результат согласуется с (П.10.46).
13.8. На осциллятор с затуханием действует периодическая сила f0 e−iωt . Найти разность фаз между смещением осциллятора и
приложенной силой при слабом затухании.
На тело массой m действует периодическая сила, упругая сила −κ x и сила вязкого трения −r x , где κ – коэффициент жесткости;
r – коэффициент трения. Второй закон Ньютона дает
|
|
x + |
2 x |
+ω02 x = q0 e−iωt , |
|
(П.13.13) |
||||||
|
|
|
|
τ |
|
|
|
|
|
|
|
|
где |
|
|
|
|
|
|
|
|
f |
|
|
|
|
r |
≡ |
2 |
; |
2 |
|
κ |
; q |
|
0 |
. |
|
|
|
|
ω |
≡ |
|
≡ |
|
|
||||
|
|
|
|
|
|
|||||||
|
m |
|
τ |
|
0 |
|
m |
0 |
|
m |
|
|
|
|
|
|
|
|
|
|
|||||
При r = 0 и q0 = 0 уравнению (П.13.13) удовлетворяет решение в виде свободных незатухающих колебаний
x(t) = x0 cos(ω0t +ϕ0 ) ,
370
ПРИМЕРЫ 13
где ω0 – частота свободных колебаний. При q0 = 0 уравнению (П.13.13) удовлетворяет решение в виде затухающих колебаний
x(t) = x1 e−t/τ cos(ω1t +ϕ1) ,
где ω1 = 
 ω02 −τ−2 – частота затухающих колебаний; τ – время затуха-
ω02 −τ−2 – частота затухающих колебаний; τ – время затуха-
ния. Уравнению (П.13.13) удовлетворяет решение в виде вынужденных колебаний
|
x(t) = A eiωt = |
q0 |
|
e−i(ωt+ϕ) , |
|
(П.13.14) |
|||||
|
| Z |
| |
|||||||||
|
|
|
|
|
|
|
|
|
|
||
где амплитуда |
|
|
|
|
|
|
|
|
|
|
|
|
A = |
|
q0 |
|
|
|
≡ q0 ; |
|
|
||
|
ω2 −ω2 + 2ωi / τ |
|
|
||||||||
|
|
|
Z |
|
|
||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
импеданс |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Z = |
| Z | eiϕ ; | Z | = |
(ω2 |
−ω2 )2 + 4(ω/ τ)2 |
; |
|||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
фаза |
|
|
|
|
|
|
|
|
|
|
|
|
|
tg ϕ = |
|
|
2ω |
|
|
. |
|
(П.13.15) |
|
|
|
τ(ω2 −ω2 ) |
|
||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
Понятие «комплексное сопротивление», или импеданс Z, ввел Оливер |
|||||||||||
Хевисайд в 1886 г. |
|
|
|
|
|
|
|
|
|
|
|
Для слабого затухания τ → ∞ при ω< ω0 ≈ ω1 |
из (П.13.15) полу- |
||||||||||
чаем tg ϕa → +0 , |
тогда угол отставания смещения от вынуждающей |
||||||||||
силы ϕa → 0 . При ω > ω0 |
находим tg ϕb → −0, тогда ϕb → π. Следо- |
||||||||||
вательно, если частота вынуждающей силы ниже частоты свобод-
ных колебаний осциллятора со слабым затуханием, то смещение осциллятора и сила совпадают по фазе. Если частота силы выше частоты свободных колебаний, то смещение осциллятора происходит в противофазе с вынуждающей силой.
371
