Донорная примесь в полупроводнике

Атом-донор полупроводника отдает валентный электрон в состав электронного газа примесной проводимости n-типа, и становится ионом с зарядом +е. Ион притягивает электронный газ и его концентрация зависит от расстояния r до иона. При температуре полупроводника T и средней концентрации свободных электронов найдем распределение потенциала и концентрации электронов вокруг донорной примеси, а также размеры области полупроводника, где существенно электрическое поле донора.

Начало координат выбираем в точке, где находится ион, тогда его распределение плотности заряда. Электрическое поле иона изменяет концентрацию электронного газа. Возникает избыточная, по сравнению со средним значением, плотность заряда

,

где – средняя концентрация электронов проводимости на большом расстоянии от иона. Результирующая плотность заряда

.

Распределение потенциала связано с распределением заряда уравнением Пуассона

.

Для рассматриваемой задачи получаем

, (П.7.13а)

где ε – диэлектрическая проницаемость материала полупроводника. Из равенства электрохимических потенциалов разных точек в состоянии равновесия системы

с учетом

, ,

следует распределение Больцмана

.

При относительно высокой температуре разлагаем экспоненту в ряд по малому показателю и оставляем первые два слагаемые

,

тогда

. (П.7.13б)

Уравнение Пуассона (П.7.13а)

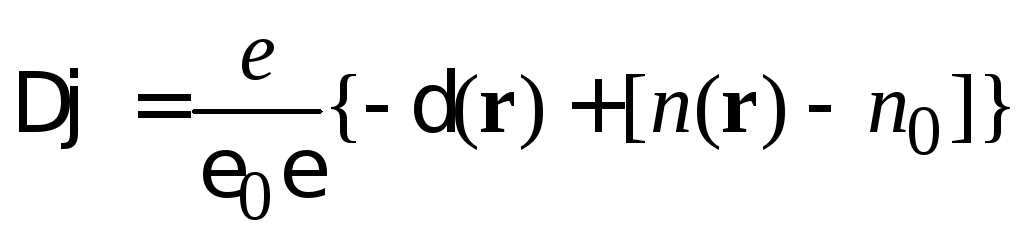
получает вид

.

Перестановка слагаемых дает трехмерное уравнение Гельмгольца с правой частью в виде дельта-функции

,

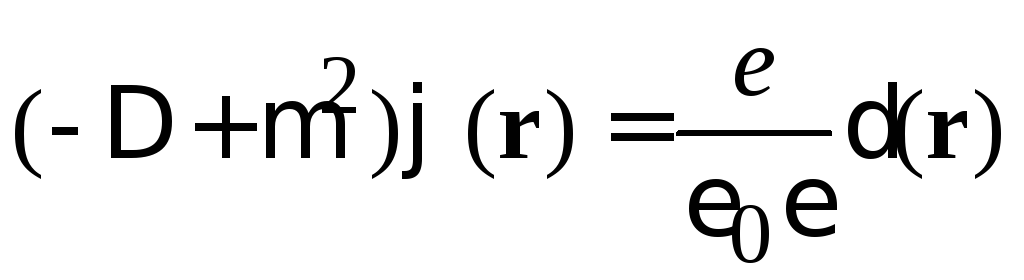где волновое число

.

Решение уравнения. Дифференциальное уравнение с постоянными коэффициентами решаем методом преобразования Фурье. Используем

,

,

.

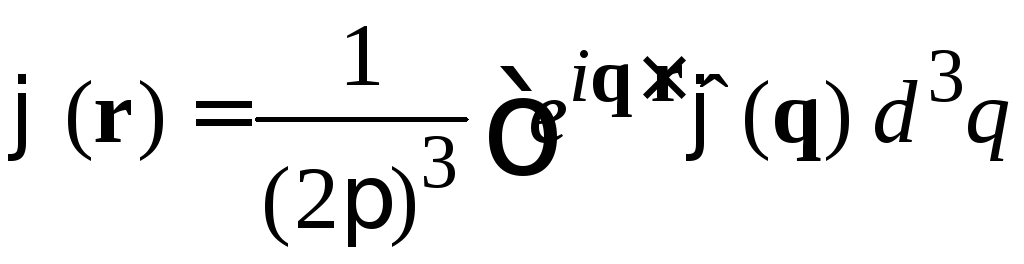Подстановка в уравнение

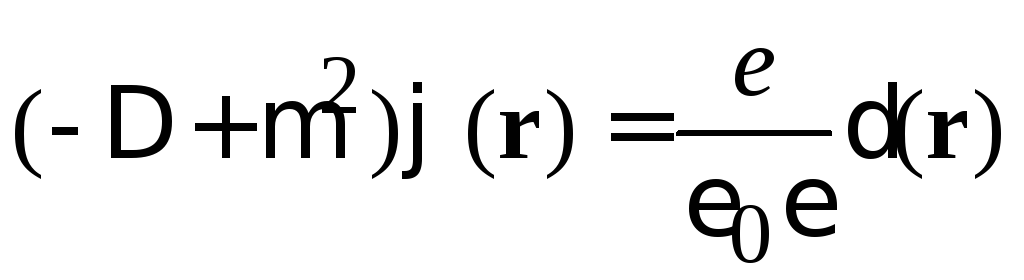
дает

.

Сравниваем подынтегральные функции и находим фурье-образ потенциала

,

где q – волновой вектор. Обратным преобразованием Фурье получаем потенциал

.

При вычислении интеграла используем в пространстве волнового вектора q сферические координаты с осью вдоль вектораr, тогда

,

,

.

Полагаем и интегрируем по углу φ

.

Вычисляем интеграл

,

тогда

.

Во втором интеграле заменяем q  –q

,

получаем

. (П.7.13в)

Вычисление интеграла

проводим при помощи теории вычетов. Контур интегрирования в комплексной плоскости проходит вдоль вещественной оси. С учетом замыкаем контур в верхней полуплоскости, как показано на рисунке.

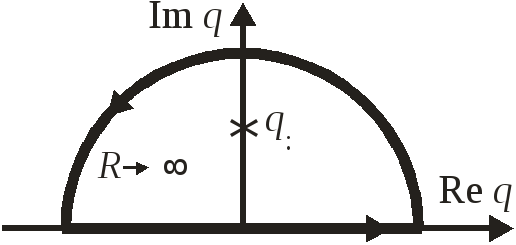
Это обеспечивает зануление подынтегральной функции

на дуге контура интегрирования при

, , .

Действительно, поскольку , то

,

.

В результате интеграл по контура сводится к интегралу по вещественной оси. Внутри контура находится полюс в точке

.

Вычет в полюсе для подынтегральной функции

,

где

,,

ищем по формуле

.

Находим

.

По теореме о вычетах интеграл равен

.

Из (П.7.13в)

получаем распределение потенциала вокруг донорной примеси

. (П.7.14)

Анализ решения. Отклонение концентрации от среднего значения с учетом (П.7.13б)

и (П.7.14) равно

.

Потенциал и отклонение концентрации уменьшаются в раз на расстояниирадиуса экранирования Дебая

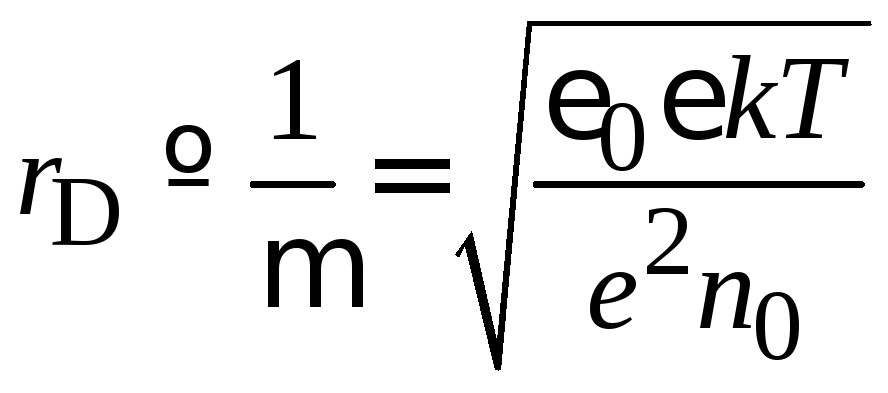. (П.7.14а)

Для кремния

, см^–3.

При К получаем

Ǻ.

Находим

,

следовательно, условие применимости решения выполняется. Радиус Дебая сравним со средним расстоянием между электронами

Ǻ.