Распределение максвелла–больцмана
Частицы идеального газа, находящиеся при температуре T в объеме V во внешнем потенциальном поле, хаотически двигаются по всем направлениям и со всеми скоростями. Получим распределения частиц по скоростям, импульсам, энергии и координатам. Распределение по скоростям без внешнего поля получил Уотерстон в 1843 г. и Максвелл в 1859 г. Распределения по импульсам и координатам во внешнем поле установил Больцман в 1866 г.
Распределение по скоростям, импульсам и энергии без внешнего поля называется распределением Максвелла. Распределение по координатам во внешнем поле – распределением Больцмана.
Распределения по координатам и импульсам
Идеальный газ из N тождественных, независимых частиц при фиксированных температуре и объеме описывается каноническим распределением
.
Плотность
вероятности распределения по фазовому
пространству микросостояний частицы
i
с гамильтонианом
равна
,
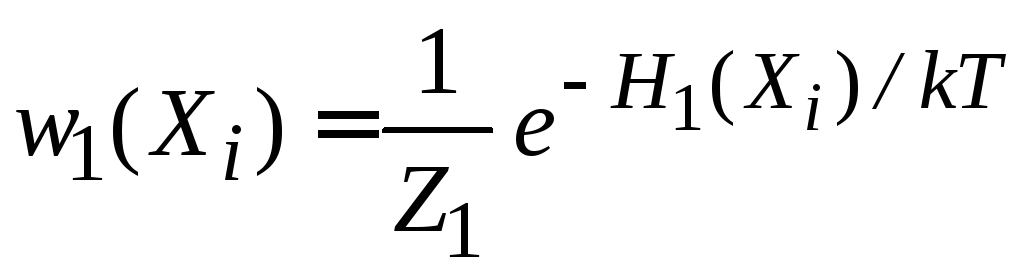где
;
.
Для
трехмерной классической частицы,
движущейся поступательно во внешнем
поле с потенциальной энергией
,
используем
,
.
Кинетическая энергия, зависящая от импульса, и потенциальная энергия, зависящая от координат, являются слагаемыми гамильтониана. В каноническом распределении гамильтониан находится в показателе экспоненты. Поэтому распределения по координатам и импульсам являются сомножителями в результирующем распределении
,
,
где
–распределение
Максвелла,
т. е. вероятность обнаружения импульса
частицы в единичном интервале около
значения p;
распределение
Больцмана,
т. е. вероятность обнаружения координаты
частицы в единичном интервале около
значения r.
Распределение Максвелла
Частица газа при температуре T может иметь тепловую скорость от очень малых до сколь угодно больших значений. Вероятности разных значений отличаются. Получим распределения по импульсам, скоростям, энергиям в декартовых и сферических координатах без внешнего поля. Для атомов учитываем лишь поступательное движение. Газ считаем трехмерным.
Распределение по импульсам
В декартовых координатах
,
,
,
каноническое распределение для частицы
получает вид
.
Интегрируем по координатам, используем
,
получаем
вероятность
обнаружения частицы газа с импульсом
в интервале
,
(2.41)
где плотность вероятности
(2.41а)
– вероятность
обнаружения частицы с проекцией импульса
на ось x
в единичном интервале около значения
и с любыми проекциями на осиy
и z.
Выполняется нормировка
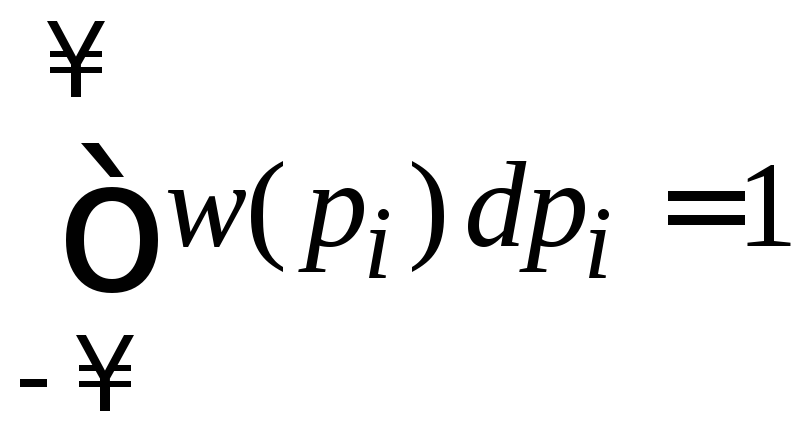
с учетом интеграла Пуассона
.
Распределение по проекции скорости
В (2.41)
заменяем импульс на скорость
,
,
находим распределение по проекциям скорости
(2.41б)
– вероятность
обнаружения частицы со скоростями в
интервале
.
Интегрируем
(2.41б) по
и
в пределах
(–¥,
¥),
используя интеграл Пуассона. Получаем
вероятность
обнаружения частицы с проекцией скорости
в интервале
,
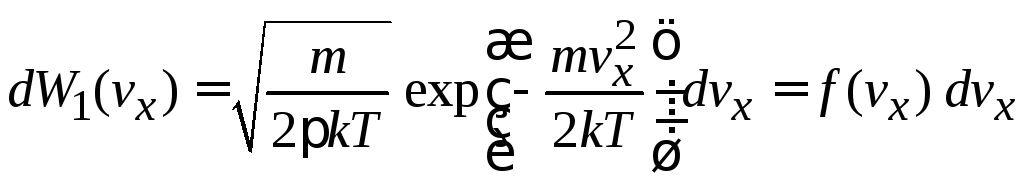(2.42)
где функция распределения по проекции скорости
(2.42а)
– относительное
число частиц с проекцией скорости в
единичном интервале около
;
n – концентрация частиц – число частиц в единице объема со всеми скоростями;
–концентрация
частиц со скоростями в интервале
около
;
–концентрация
частиц со скоростями в единичном
интервале около
.
При
функция максимальна
.
Выполняется нормировка
,
.
Следовательно:
при любой температуре площадь под кривой равна единице;
с ростом Т максимум понижается, график расширяется, увеличивается вероятность обнаружить частицу с большей скоростью;
при
с учетом
распределение становится дельта-функцией
,
частицы останавливаются.