Операторы спина электрона. Спиноры

Операторы спина аналогичны операторам момента импульса

, ,,

,

.

Коммутационные соотношения аналогичны (4.5)

,

,

,

,

, . (7.7)

Спин не связан с координатой и импульсом, поэтому коммутирует с ними. Уравнения для собственных функций взаимно коммутирующих операторов спина аналогичны (4.14)–(4.15)

,

. (7.8)

В набор квантовых чисел электрона в атоме кроме n, l, m входит спиновое число . Независимость радиального, углового и спинового движений означает, что функция состояния факторизована

.

Матрицы Паули. Поскольку проекция спина на произвольно выбранное направление двузначна , то собственную функцию операторов спинавыражаем двухэлементной матрицей –спинором

.

Операторы спина получают матричную форму

, ,,, (7.9)

где матрицы Паули

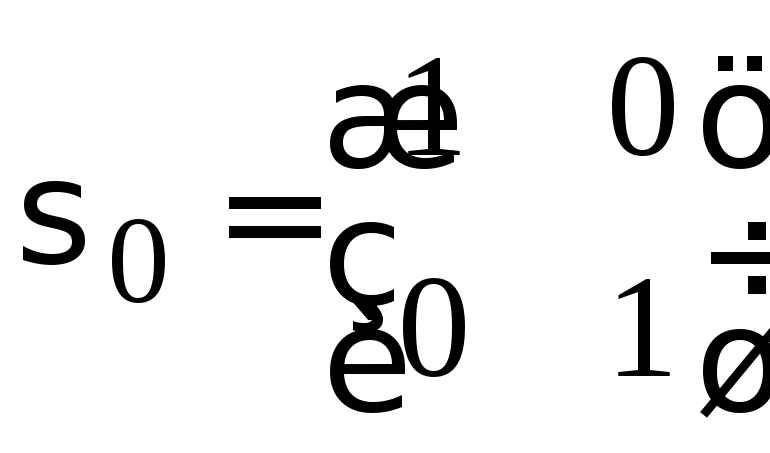, ,,,(7.10)

,

где – единичная матрица, получены из условия выполнения коммутационных соотношений (7.7) для операторов спина. Действительно, выполняются соотношения для матриц Паули

,

,

,

,

,

,

, ,,

, ,

, ,, (7.11)

и для операторов спина

,

,

, ,.

Эрмитовое сопряжение «+» матрицы включает комплексное сопряжение * и транспонирование T ее элементов

. (7.12)

Операторы спина и матрицы Паули эрмитовые

, .

Например, для

находим

.

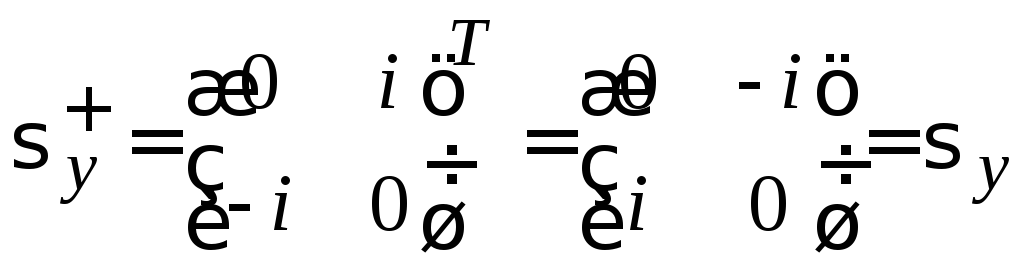Матрицы Паули унитарные и удовлетворяют

.

Результат следует из эрмитовости и соотношения.Под действием унитарного оператора состояния систем поворачиваются в гильбертовом пространстве, при этом сохраняются скалярные произведения состояний и их нормировка.

Нормировка и ортогональность спиноров

, .

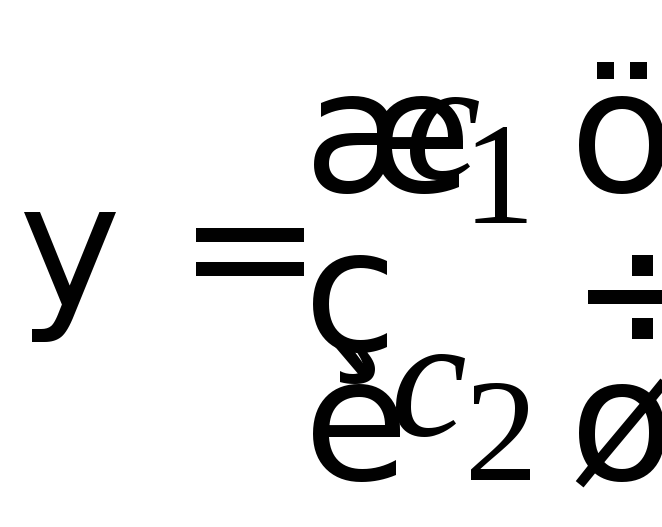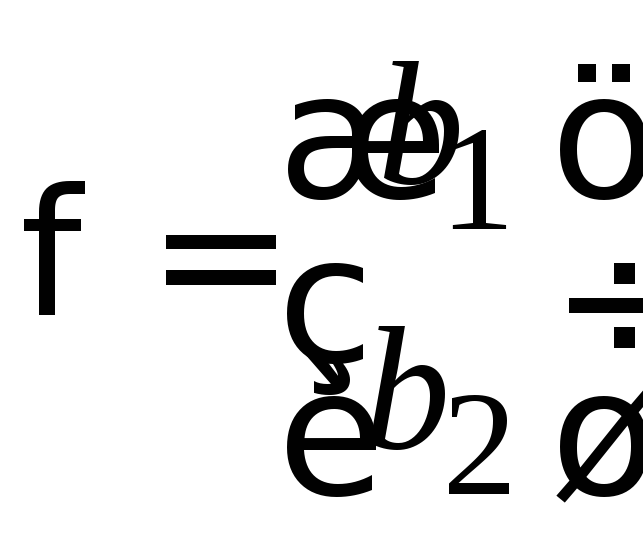При транспонировании, комплексном сопряжении и эрмитовом сопряжении

, ,.

Определяем скалярное произведение спиноров

,

тогда условие нормировки

, (7.13)

условие ортогональности

. (7.14)

Среднее значение проекции спина на ось k по нормированному состоянию  определяется в виде

. (7.15)

Собственные функции оператора. Для оператора

собственную функцию и собственное значение находим из уравнения

.

Решение ищем в виде

.

Подстановка в уравнение

дает

.

Сравниваем элементы матриц и получаем систему алгебраических уравнений

,

.

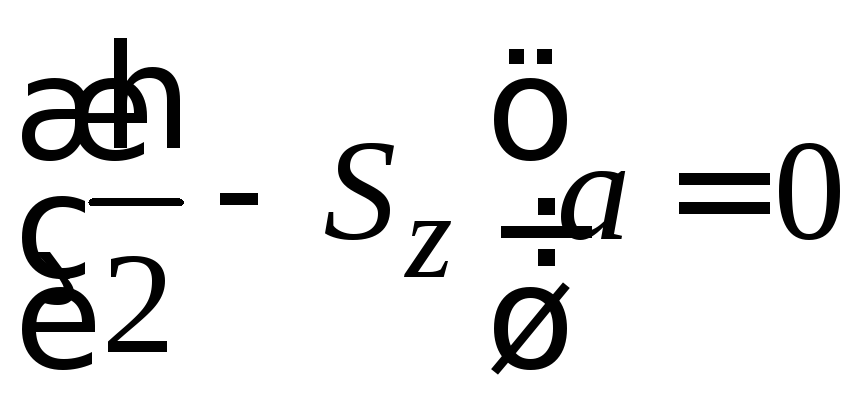При находим

, ,.

При

, ,.

Нормировка (7.13)

с точностью до постоянного фазового множителя дает взаимно ортогональные собственные функции оператора

, ;

, ;

, . (7.16)

Произвольное спиновое состояние разлагается по этому ортонормированному базису

,

,

. (7.17)

Вероятности обнаружения проекций спина

,

. (7.18)

Свободный электрон со спином, направленным по оси z, с энергией Е и импульсом р описывается спинором

. (7.19)

Плотность тока вероятности (2.71)

для спинора записывается в виде

.

Комплексное сопряжение заменяется на эрмитовое сопряжение.

Оператор полного момента

описывает частицу со спином , совершающую орбитальное движение с моментом импульса. Гамильтониан коммутирует с операторами

, ,

, ,

поэтому их собственные значения определены вместе с энергией и характеризуют состояние частицы. Собственные функции и собственные значения полного момента удовлетворяют

.

В состоянии с квантовыми числами

из

получаем

.

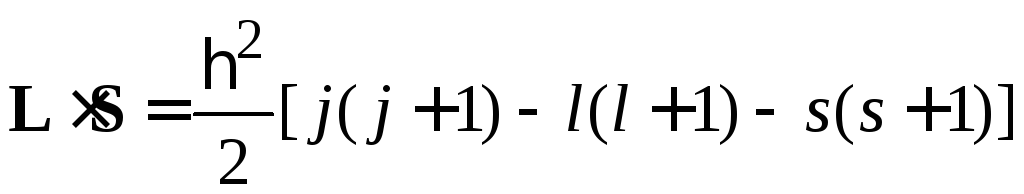Векторная сумма ограничивает возможные значения квантовых чисел

.

Для электрона получаем

.

Проекция полного момента на произвольное направление описывается оператором и квантуется аналогично (4.15)

, .

Состояние электрона в атоме в приближении одночастичных состояний, когда каждый электрон находится в определенном состоянии, обозначается символом Рассела–Саундерса

,

где n – главное квантовое число; состояния с обозначаются буквами;– число спиновых проекций. Например, при,разрешенные состояния электрона сиобозначаютсяи.

Электронная конфигурация атома. В обозначении перечисляются все занятые электронные оболочки, то есть состояния с определенными числами (n,l) в порядке возрастания. Вначале ставится главное число и для каждогоn перебираются всевозможные значения орбитального числа . Для каждой оболочкиl указывается вверху справа число заполняющих электронов, равное . Это число равно произведению числа проекций спина и числа проекции орбитального момента. Например, для кремния св основном состоянии электронная конфигурация:.

Состояние атома как целого описывает символ

,

где L – полное орбитальное число атома; S – полный спин атома; J – полный момент атома.

Множитель Ланде для атома вычисляется по формуле

.