Статистический смысл энтропии

Из (2.67) и (2.68)

,

находим

, (2.70)

\Интегрируем

.

Выбираем , тогда система в одном микросостоянииимеет нулевую энтропию в соответствии с третьим началом термодинамики. В результате

, (2.71)

Получен статистический смысл энтропии – энтропия пропорциональна логарифму числа микросостояний фазового ансамбля. Из (2.68) и (2.71) получаем

. (2.71а)

Фазовый объем системы, состоящей из независимых подсистем 1 и 2, равен произведению объемов, которые они занимают:

.

Из (2.71) получаем аддитивность энтропии

(2.72)

– энтропия системы равна сумме энтропий независимых подсистем.

Из (2.20) и (2.70)

,

находим

.

Используем (2.68)

,

получаем

. (2.73)

Из приведенных соотношений следует:

1. Согласно (2.71)

выполняется

, (2.74)

число микросостояний фазового ансамбля системы увеличивается экспоненциально с ростом энтропии.

2. Чем больше возможных микросостояний, реализующих макросостояние, тем меньше информации о системе. Увеличение энтропии означает уменьшение информации о системе и увеличение ее хаотичности. Чем более упорядочена система, тем меньше ее энтропия. Для контроля и управления системой необходимо снижать ее энтропию.

3. Согласно (2.73) чем ниже температура, тем быстрее уменьшается энтропия с понижением энергии системы. Для уменьшения энтропии следует снижать температуру и использовать переходы с малой энергией. Согласно теореме Нернста, или третьему началу термодинамики, при у любой системыи она занимает лишь одно микросостояние.

4. Для замкнутого обратимого процесса выполняется равенство Клаузиуса

,

или второе начало термодинамики. Следовательно, энтропия является функцией состояния.

Пример 1

Атом массой m с гамильтонианом и энергией находится в трехмерном изолированном объеме V, где все точки и направления равноправны. Найти макрохарактеристики фазового ансамбля. Рассмотреть газ из N атомов.

Система изолирована, тогда

, .

Фазовый ансамбль микросостояний частицы находится в импульсном пространстве на трехмерной сфере радиусом

.

Микросостояния отличаются направлениями вектора импульса и положениями в объеме V. Число микросостояний системы при отсутствии внешнего поля выражает (2.2б)

.

При ,получаем

.

Используем объем шара

,

находим число микросостояний

. (П.2.4)

Энергетическая плотность состояний частицы (2.22)

равна

. (П.2.5)

Плотность состояний классической частицы пропорциональна объему V, доступному для частицы, и корню квадратному из энергии.

Энергетическая плотность состояний частицы

Из (2.68)

и (П.2.4), (П.2.5)

,

находим тепловую энергию

. (П.2.6)

Следовательно, средняя энергия частицы, пропорциональная тепловой энергии

.

При нормальной температуре

.

Из (2.64), (П.2.5)

,

и (П.2.4)

,

находим давление, создаваемой фазовым ансамблем, соответствующим одной частице:

,

где учтено (П.2.6) . Получено уравнение идеального газа из одной частицы.

Энтропию находим из (2.71) и (П.2.4)

, ,

получаем

,

где .Для понижения энтропии нужно уменьшать объем сосуда и энергию частицы.

Частный случай – азот N₂. Масса атома

кг.

При

л, С,

получаем

эВ,

1/эВ.

На интервале энергии эВ находятсяуровней, следовательно,классический газ имеет квазинепрерывный спектр энергии.

Для N одинаковых частиц идеального газа полная энергия складывается из энергий отдельных частиц

,

где – проекция импульса одной из частиц на декартову ось. В 3N-мерном импульсном пространстве получаем уравнение сферы радиусом . Объема шара вычисляем по формуле(П.2.1)

, .

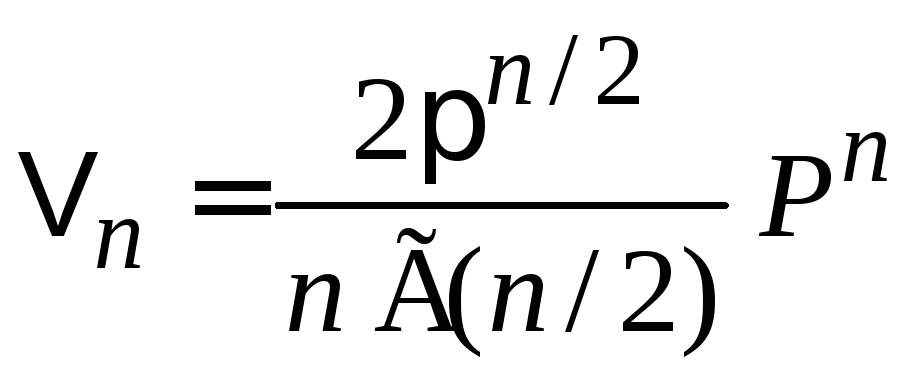Получаем

,

,

тогда

,

.

Из (2.68) находим

– температура пропорциональна средней энергии частицы.

Давление

удовлетворяет уравнению идеального газа

.