Химический потенциал и теплоемкость сильно вырожденного трехмерного электронного газа

Для металлов при К с учетом значений химического потенциала

эВ, эВ,

выполняется . Следовательно, электронный газ металла вырожден. Для такого газа найдем зависимость химического потенциала и теплоемкости от температуры.

Число электронов (4.15)

не зависит от температуры. При находим

.

При используемразложения Зоммерфельда

, (П.10.20)

получаем

.

Приравниваем результаты

.

Близость идает

,

тогда

. (П.10.24)

Для трехмерного газа с учетом (3.7) находим

. (П.10.24а)

Выполняется

, .

С увеличением температуры от нуля до химический потенциал сильно вырожденного трехмерного электронного газа уменьшается. Для большого интервала температур график (Т) показан на рис. 4.3.

Внутренняя энергия газа

,

.

Используя (П.10.20)

,

вычисляем интеграл

.

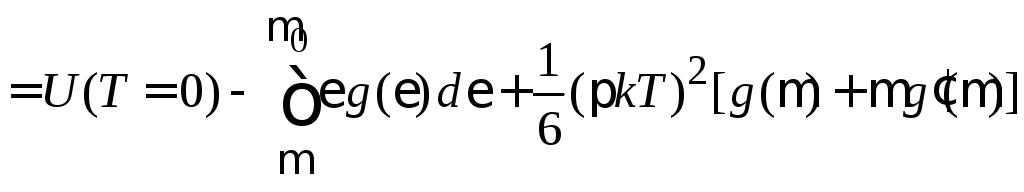Используя близость и, получаем

.

Из (П.10.24) выражаем

.

В результате

. (П.10.25)

Из (П.10.25) находим

, (П.10.26)

где –постоянная Зоммерфельда. Теплоемкость сильно вырожденного f-мерного электронного газа пропорциональна плотности состояний и первой степени температуры. При получаем, что согласуется с третьим началом термодинамики.

Для трехмерного газа из N частиц с учетом (4.23) и (4.28)

из (П.10.25) получаем

. (П.10.26а)

Второе слагаемое по порядку величины равно . Первая скобка является тепловой энергией электрона. Вторая скобка равна числу активированных электронов в полосе энергии ширинойkT около уровня Ферми. Только эти электроны дают вклад в теплоемкость и их доля мала при . Из (П.10.26) находим

. (П.10.26б)

Для серебра .Теплоемкость электронного газа металла пренебрежимо мала по сравнению с теплоемкостью кристаллической решетки, равной .

Двухмерный электронный газ

Технологии литографии и молекулярно-лучевой эпитаксии дают возможность создавать полупроводниковые структуры микроскопического размера с заданными свойствами. Структура ограничивает носители тока пределами потенциальной ямы. Спектр энергии дискретный. Уменьшение ширины ямы увеличивает энергии уровней и расстояния между ними. Ограничение по одному направлению с размером меньшим длины свободного пробега носителя тока дает двухмерный газ (2D-газ), ограничение по двум направлениям создает одномерный газ (1D-газ), ограничение по трем направлениям – квантовую точку.

Состояния с одинаковой энергией, отличающиеся другими квантовыми числами – проекцией спина, проекциями импульса, образуют разрешенную зону. В узком проводнике с малой концентрацией носителей тока уровень Ферми превышает лишь первый уровень ямы, и носители тока при малой температуре заполняют нижнюю зону. При длине проводника, меньшей длины свободного пробега носителя тока, фаза его волновой функции изменяется регулярно без скачков. Волны, разделившиеся и прошедшие по разным путям, интерферируют в точке наложения волн. Такая полупроводниковая структура называется мезоскопической системой пониженной размерности.

Для исследования и применения низкоразмерных явлений широко используется гетероструктура , показанная на рис. 4.6.

Рис. 4.6. Гетероструктура.

L– область двухмерного электронного газа,SиD– электроды

В твердом растворе доля С атомов галлия замещена атомами алюминия. При различие периодов кристаллических решеток составляет менее десятой доли процента. При изготовлении гетероструктуры вводятся легирующие примесные атомы Si в . Они являются донорами и их помещают на расстоянии в несколько десятков нанометров от границы с . Электроны из легированной области мигрируют в область , сбрасывают избыток энергии, и скапливаются на дне зоны проводимости , показанной темной областью на рисю 4.7,а. Положительный заряд ионизированных доноров притягивает электроны к границе. По одну сторону образуется положительный заряд в , по другую – отрицательный заряд в . Энергетические зоны полупроводников изгибаются, как показано на рис. 4.7, в зоне проводимости возникает потенциальная ямашириной нмс двухмерным электронным газом.

а б

Рис. 4.7. Энергетические зоны в гетероструктуре

Толщину слоя L и концентрацию электронов можно изменять при помощи дополнительного электрода – затвора на гетероструктуре, размещенного на поверхности , подавая на него потенциал мВ.В направлении оси z движение электронов ограничено, вдоль границы они движутся свободно. Такой двухмерный электронный газ имеет высокую подвижность, превышающую подвижность трехмерного газа в на один–два порядка. Это объясняется малой эффективной массой электронов и тем, что легирующие атомы Si, расположенные неупорядоченно и являющиеся центрами рассеяния, находятся вдали от потенциальной ямы. Рассматриваемую гетероструктуру предложили Есаки и Тсу в 1969 г.

Лео Эсаки, род. 1925 г.

Параметры гетероструктуры приК, с долей замещенных атомов :

поверхностная концентрация электронов см^–2;

эффективная масса ;

длина волны де Бройля нм;

длина свободного пробега мкм;

ширина ямы нм;

подвижность см² В^–1 с^–1;

энергия Ферми эВ.

Получим химический потенциал и распределение по энергии электрона с учетом поперечного квантования по оси z.

Закон дисперсии в слое

,

где – импульс в плоскости слоя;– квантованная энергия поперечного движения. Для прямоугольной ямы ширинойL с непроницаемыми стенками

,

где – номер зоны поперечного квантования. При малой толщине слояL энергия Ферми находится между первым и вторым уровнями ямы

,

и все электроны располагаются в нижней зоне .

Распределение электронов по энергии. Плотность состояний в пленке на единице площади при находим из (П.8.4а)

.

Для распределения Ферми–Дирака

,

получаем число электронов на единице площади с энергией в единичном интервале около значения ε

. (4.31)

Все носители заряда находятся в нижней зоне, тогда поверхностная концентрация электронов

. (4.32)

В интеграле заменяем и находим

,

получаем

, (4.33)

выражаем химический потенциал

. (4.34)

Химический потенциал растет с увеличением поверхностной концентрации электронов, с уменьшением эффективной массы и слабо зависит от температуры.

Из (4.31)

получаем вероятность того, что электрон имеет энергию в интервале

. (4.34а)

Вырожденный газ соответствует высокой концентрации, низкой температуре и малой массе частицы. Для примесной n-проводимости GaAs с поверхностной концентрацией см^–2 эффективная масса на дне зоны проводимости , тогда ужепри комнатной температуре выполнено условие вырождения

. (4.35)

В (4.34)

пренебрегаем единицей в круглой скобке

,

получаем

. (4.36)

Химический потенциал вырожденного двухмерного газа линейно зависит от поверхностной концентрации электронов, обратно пропорционален эффективной массе и не зависит от температуры.

Условие, что все электроны находятся в нижней зоне

,

с учетом (4.36) ограничивает концентрацию

. (4.37)

Используя

, ,

из (4.37) находим

.

Для n-GaAs с см^–2 ограничение на толщину пленки дает нм.

Из (4.36)

получаем импульс Ферми

, (4.38)

и минимальную длину волны де Бройля в газе

.

Учитывая

,

где d – характерное расстояние между частицами, получаем

.

Следовательно, волновые функции соседних частиц перекрываются, существенна интерференция между ними, и газ вырожденный.